So berechnen sie ein skalarprodukt auf einem ti-84-rechner

Gegeben sei der Vektor a = [a ₁ , a ₂ , a ₃ ] und der Vektor b = [b ₁ , b ₂ , b ₃ ], das Skalarprodukt des Vektors a und des Vektors b, bezeichnet mit ab , ist gegeben durch:

ab = a ₁ * b ₁ + a ₂ * b ₂ + a ₃ * b ₃

Wenn beispielsweise a = [2, 5, 6] und b = [4, 3, 2], dann wäre das Skalarprodukt von a und b gleich:

ab = 2*4 + 5*3 + 6*2

ab = 8 + 15 + 12

ab = 35

Wir können die folgende Syntax verwenden, um das Skalarprodukt zweier Vektoren auf einem TI-84-Rechner zu berechnen:

 sum ({2, 5, 6} * {4, 3, 2})

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie Sie diese Syntax in der Praxis anwenden können.

Beispiel: Berechnen Sie das Skalarprodukt mit dem TI-84-Rechner

Führen Sie die folgenden Schritte aus, um das Skalarprodukt zwischen zwei Vektoren zu berechnen:

Schritt 1: Geben Sie den Befehl sum( ein.

Drücken Sie zuerst 2nd , dann STAT, scrollen Sie dann zu MATH und drücken Sie sum :

Schritt 2: Geben Sie die linke Klammer ein.

Drücken Sie dann die 2. Taste und dann (, um die erste geschweifte Klammer einzugeben:

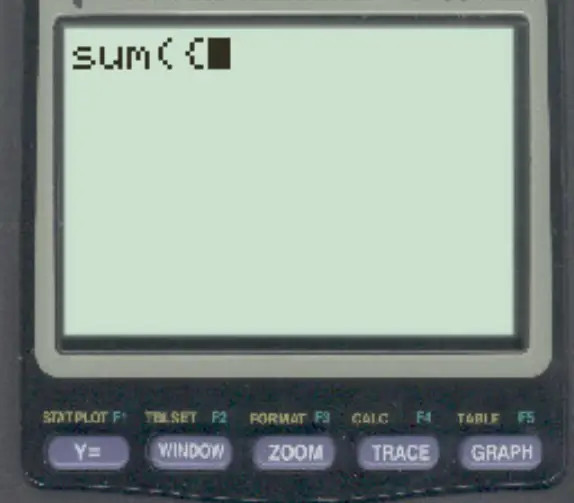
Schritt 3: Geben Sie die Daten ein

Geben Sie als Nächstes für jeden Vektor die folgenden Werte ein:

• Vektor a: 2, 5, 6
• Vektor b: 4, 3, 2

Stellen Sie sicher, dass Sie zwischen den beiden Vektoren ein Multiplikationszeichen einfügen und schließen Sie den Befehl sum() mit einer rechten Klammer ab. Drücken Sie dann ENTER :

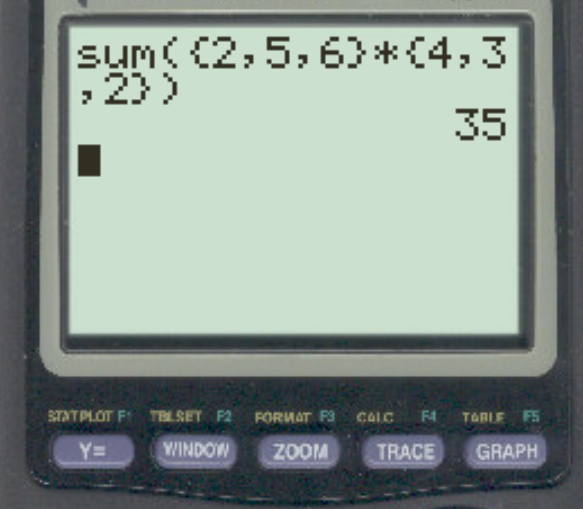
Das Skalarprodukt ergibt sich zu 35 . Dies entspricht dem von uns manuell berechneten Wert.

Zusätzliche Ressourcen

So berechnen Sie das Skalarprodukt in Excel
So berechnen Sie das Skalarprodukt in Google Sheets
So berechnen Sie das Skalarprodukt in R