Normal- oder gleichverteilung: was ist der unterschied?

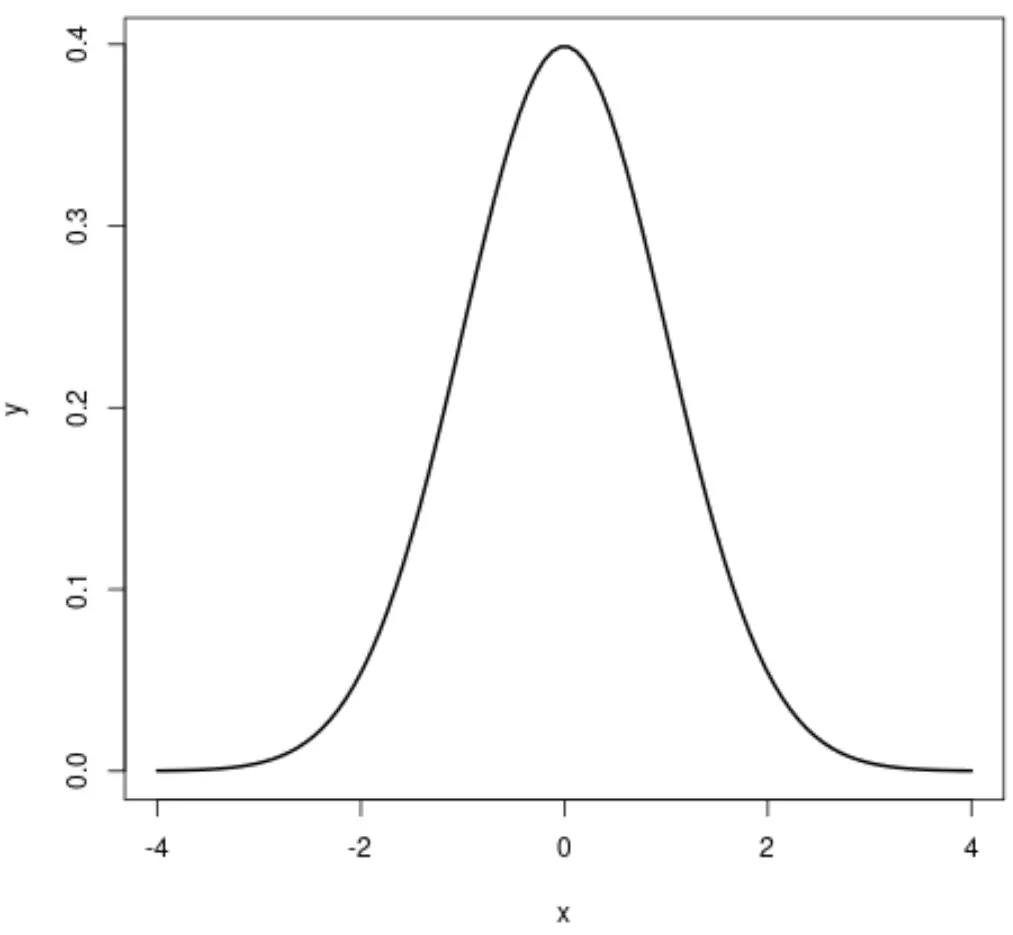
Die Normalverteilung ist die in der Statistik am häufigsten verwendete Wahrscheinlichkeitsverteilung.

Es hat die folgenden Eigenschaften:

• Symmetrisch
• Glockenförmig

Wenn wir ein Diagramm der Normalverteilung erstellen, sieht es folgendermaßen aus:

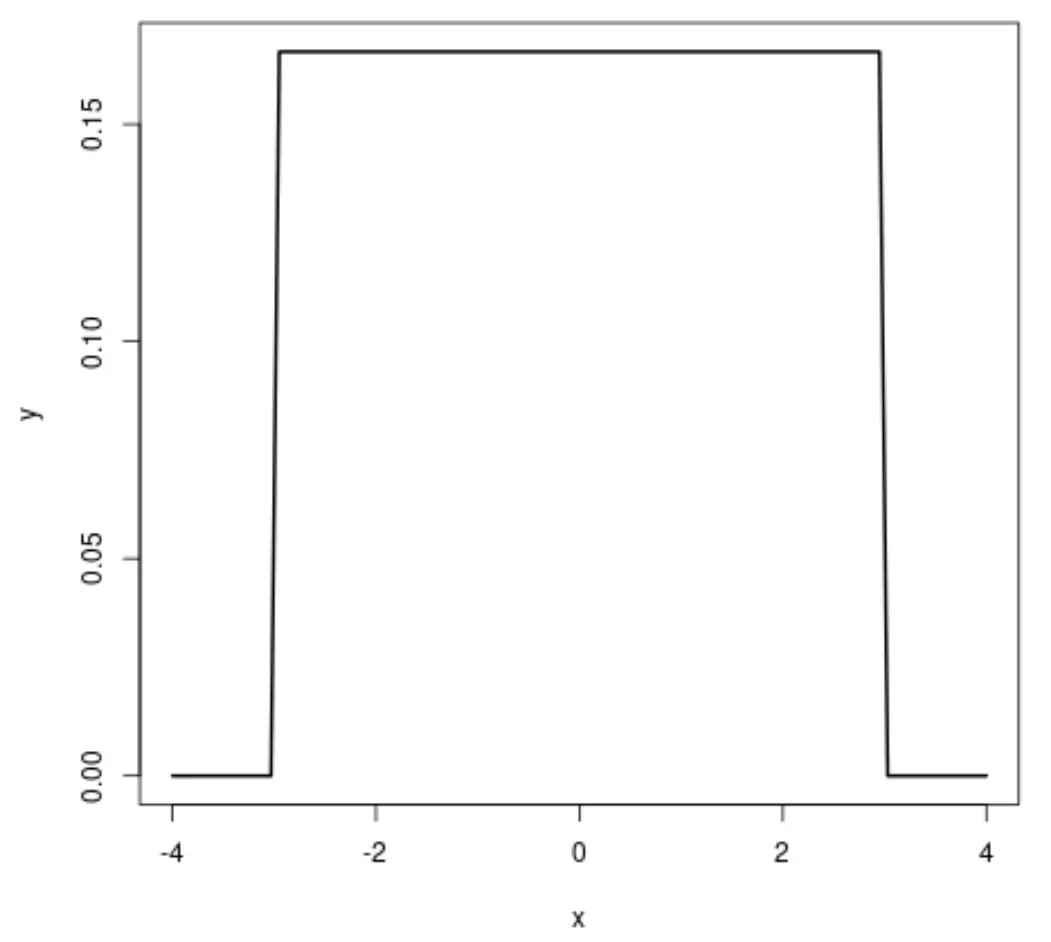
Die Gleichverteilung ist eine Wahrscheinlichkeitsverteilung, bei der jeder Wert zwischen einem Intervall von a bis b die gleiche Eintrittswahrscheinlichkeit hat.

Es hat die folgenden Eigenschaften:

• Symmetrisch
• Rechteckige Form

Wenn wir ein Diagramm der Gleichverteilung erstellen, sieht es folgendermaßen aus:

Die Normalverteilung und die Gleichverteilung haben folgende Ähnlichkeit :

• Die beiden Verteilungen sind symmetrisch. Das heißt, wenn wir eine Linie durch die Mitte der Verteilung ziehen würden, würden sich die linke und rechte Seite der Verteilung perfekt spiegeln:

Die beiden Verteilungen weisen jedoch den folgenden Unterschied auf:

• Die Verteilungen haben unterschiedliche Formen.
• Die Normalverteilung ist glockenförmig, was bedeutet, dass Werte in der Nähe der Verteilungsmitte mit größerer Wahrscheinlichkeit auftreten als Werte am Ende der Verteilung.
• Die Gleichverteilung hat eine rechteckige Form, was bedeutet, dass jeder Wert in der Verteilung die gleiche Eintrittswahrscheinlichkeit hat.

Normalverteilung oder Gleichverteilung: Wann werden sie verwendet?

Die Normalverteilung wird zur Modellierung von Phänomenen verwendet, die dazu neigen, einer „Glockenkurve“-Form zu folgen. Es ist beispielsweise gut dokumentiert, dass das Geburtsgewicht von Neugeborenen normalerweise im Durchschnitt bei etwa 7,5 Pfund liegt.

Das Histogramm des Geburtsgewichts von Neugeborenen in den Vereinigten Staaten weist eine Glockenform auf, die im Allgemeinen der Normalverteilung entspricht:

Die meisten Babys wiegen wahrscheinlich etwa 7,5 Pfund, wobei einige weniger als 7 Pfund und einige mehr als 8 Pfund wiegen.

Umgekehrt wird die Gleichverteilung zur Modellierung von Szenarien verwendet, in denen jedes potenzielle Ergebnis gleich wahrscheinlich ist.

Ein klassisches Beispiel ist das Würfeln. Wenn Sie einen Würfel einmal würfeln, folgt die Wahrscheinlichkeit, dass er auf eine Zahl zwischen 1 und 6 fällt, einer Gleichverteilung, da jede Zahl die gleiche Wahrscheinlichkeit hat, zu erscheinen.

Es gibt beispielsweise 6 mögliche Zahlen, auf denen der Würfel landen kann, sodass die Wahrscheinlichkeit, dass Sie eine 1 würfeln, 1/6 beträgt.

Ebenso beträgt die Wahrscheinlichkeit, dass Sie eine 2 würfeln, 1/6.

Ebenso beträgt die Wahrscheinlichkeit, dass Sie eine 3 würfeln, 1/6.

Und so weiter.

Bonus: So zeichnen Sie die Normal- und Gleichverteilung auf

Wir haben den folgenden Code in R verwendet, um Diagramme der Normal- und Gleichverteilungen zu erstellen:

 #define x-axis
x <- seq(-4, 4, length=100)

#calculate normal distribution probabilities
y <- dnorm(x)

#plot normal distribution
plot(x, y, type = " l ", lwd = 2 )

#define x-axis
x <- seq(-4, 4, length=100)

#calculate uniform distribution probabilities
y <- dunif(x, min = -3, max = 3)

#plot uniform distribution
plot(x, y, type = " l ", lwd = 2 , xlim = c(-4, 4))

Zusätzliche Ressourcen

6 konkrete Beispiele der Normalverteilung
5 konkrete Beispiele für Gleichverteilung
Symmetrische Verteilung: Definition + Beispiele