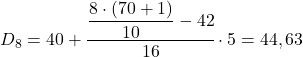Déciles
Dans cet article, nous expliquons ce que sont les déciles et comment ils sont calculés. Vous trouverez également plusieurs exemples résolus étape par étape de calculs de déciles et, en outre, vous pourrez calculer les déciles de n’importe quel échantillon statistique avec un calculateur en ligne.
Que sont les déciles ?
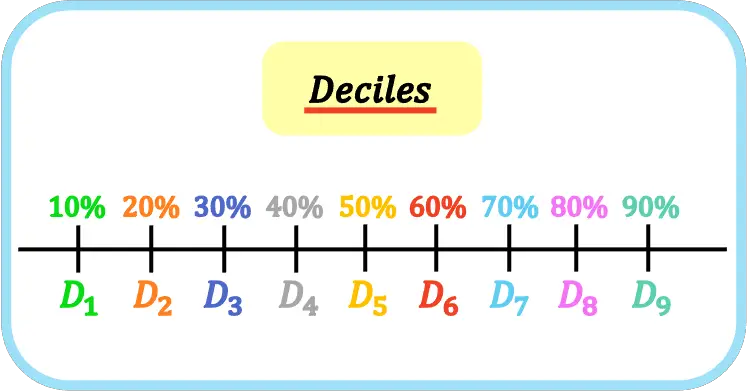
En statistiques, les déciles sont les neuf valeurs qui divisent un ensemble de données ordonnées en dix parties égales. De sorte que le premier, deuxième, troisième,… décile représente 10%, 20%, 30%,… de l’échantillon ou de la population.
Par exemple, la valeur du quatrième décile est supérieure à 40 % des données, mais inférieure au reste des données.
Les déciles sont représentés par la lettre majuscule D et l’indice du décile, c’est-à-dire que le premier décile est D 1 , le deuxième décile est D 2 , le troisième décile est D 3 , etc.
👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer les déciles pour n’importe quel ensemble de données.
Il convient de noter que les déciles sont une mesure de la position non centrale au même titre que les quartiles, les quintiles et les centiles. Vous pouvez vérifier la signification de chacun de ces types de quantiles sur notre site Web.
De plus, le cinquième décile équivaut à la médiane et au deuxième quartile, puisqu’ils divisent l’ensemble des données en deux parties égales.
Comment calculer les déciles
Pour calculer la position des déciles d’une série de données statistiques, il faut multiplier le numéro du décile par la somme du nombre total de données plus un et diviser le résultat par dix.
La formule des déciles est donc :
![]()
Attention : cette formule nous indique la position du décile, pas la valeur du décile. Le décile sera la donnée située à la position obtenue par la formule.
Cependant, parfois le résultat de cette formule nous donnera un nombre décimal, il faut donc distinguer deux cas selon que le résultat est un nombre décimal ou non :
- Si le résultat de la formule est un nombre sans partie décimale , le décile est la donnée qui se trouve dans la position fournie par la formule ci-dessus.
- Si le résultat de la formule est un nombre avec une partie décimale , la valeur du décile est calculée à l’aide de la formule suivante :
![]()
Où x i et x i+1 sont les nombres des positions entre lesquelles se trouve le nombre obtenu par la première formule, et d est la partie décimale du nombre obtenu par la première formule.
Vous pensez peut-être maintenant qu’obtenir les déciles d’un échantillon statistique est complexe, mais en pratique, c’est assez simple. Si vous lisez les deux exemples suivants, vous le comprendrez sûrement beaucoup mieux.
Remarque : la communauté scientifique n’est pas entièrement d’accord sur le calcul des déciles, vous trouverez donc peut-être des livres de statistiques qui l’expliquent un peu différemment.
Exemple de calcul de décile
Comme vous l’avez vu ci-dessus, le calcul des déciles dépend du fait que le nombre que nous donne la première formule est décimal ou non, c’est pourquoi nous avons préparé ci-dessous deux exemples résolus, un pour chaque cas. Dans tous les cas, n’oubliez pas que si vous avez des questions sur la composition des déciles, vous pouvez les poser dans les commentaires.
Exemple 1
- Étant donné les données suivantes, du plus petit au plus grand, trouvez le premier, le troisième et le huitième décile de l’échantillon.

Les données de cet exercice sont déjà triées, il n’est donc pas nécessaire de modifier l’ordre, sinon nous devrions d’abord trier les données de la plus petite à la plus grande.
Comme expliqué ci-dessus, la formule qui permet de retrouver les positions des déciles est la suivante :
![]()
La taille de l’échantillon pour cet exercice est de 29 observations, donc pour calculer la position du premier décile il faut substituer 29 à n et 1 à k :
![]()
Le résultat de la formule est 3, donc le premier décile sera en troisième position de la liste ordonnée, et cette valeur correspond à 85.
Maintenant, nous appliquons à nouveau la même procédure mais avec le troisième décile. Nous utilisons la formule en remplaçant le k par un 3 :
![]()
Le troisième décile sera donc l’élément en neuvième position, soit 97.
Finalement, on fait la même démarche mais en mettant un 8 dans la formule pour déterminer le huitième décile :
![]()
Le huitième décile sera le nombre en position 24 de la liste ordonnée des données, donc le huitième décile est 131.
Exemple 2
- À partir des données du tableau suivant, calculez les déciles 4, 7 et 9.

Comme dans l’exemple précédent, pour obtenir les positions des déciles il faut utiliser la formule suivante :
![]()
Dans ce cas, la taille de l’échantillon est de 42, donc pour trouver la position du quatrième décile il faut substituer le paramètre n par 42 et le k par 4 :
![]()
Mais cette fois, nous avons obtenu un nombre décimal à partir de la formule, nous devons donc appliquer la formule suivante pour calculer le décile exact :
![]()
Le nombre obtenu à partir de la première formule est 17,2, donc le quatrième décile est compris entre la dix-septième et la dix-huitième donnée, qui sont respectivement 109 et 112. Par conséquent, x i vaut 109, x i+1 vaut 112 et d est la partie décimale. du nombre obtenu, soit 0,2.
![]()
On répète le même processus pour trouver le septième décile. On calcule d’abord la position du décile :
![]()
De la formule nous avons obtenu le nombre 30,1, ce qui signifie que le décile sera entre les positions 30 et 31, dont les valeurs sont 154 et 159. Le calcul du décile exact est donc :
![]()
Enfin, nous appliquons à nouveau la même méthode pour obtenir le neuvième décile. On détermine la position du décile :
![]()
Le nombre obtenu est décimal et est compris entre 38 et 39, dont les positions correspondent aux valeurs 189 et 196. Ainsi le calcul du décile 9 est :
![]()
Calculateur de décile
Branchez un ensemble de données statistiques dans la calculatrice ci-dessous pour calculer les déciles. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.
Déciles en données groupées
Pour calculer les déciles lorsque les données sont regroupées en intervalles , nous devons d’abord trouver l’intervalle ou la classe dans laquelle se situe le décile à l’aide de la formule suivante :
![]()
Le décile sera donc dans l’intervalle dont la fréquence absolue est immédiatement supérieure au nombre obtenu dans l’expression précédente.
Et une fois que l’on connaît déjà l’intervalle auquel appartient le décile, il faut appliquer la formule suivante pour trouver la valeur exacte du décile :
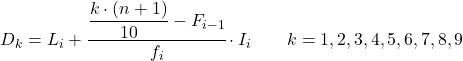
Où:
- L i est la limite inférieure de l’intervalle dans lequel se situe le décile.
- n est le nombre total de données statistiques.
- F i-1 est la fréquence absolue cumulée de l’intervalle précédent.
- f i est la fréquence absolue de l’intervalle dans lequel se situe le décile.
- I i est la largeur de l’intervalle décile.
Pour que vous puissiez voir comment cela se fait, vous avez ci-dessous un exercice complété dans lequel sont calculés les déciles 3, 5 et 8 des données suivantes regroupées par intervalles.
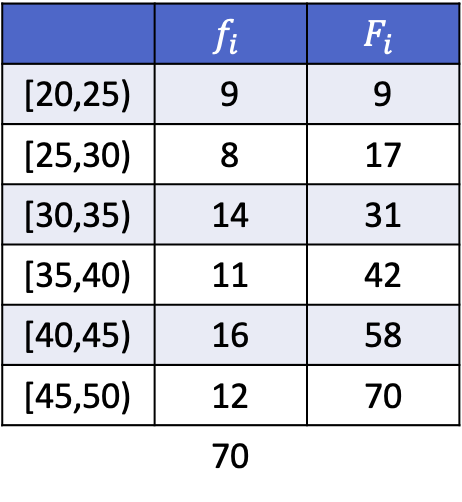
Les données étant regroupées, le calcul de chaque décile se compose de deux étapes : il faut d’abord trouver l’intervalle dans lequel se situe le décile, puis calculer la valeur exacte du décile. On retrouve donc l’intervalle du troisième décile :
![]()
![]()
L’intervalle du décile sera celui dont la fréquence cumulée absolue est immédiatement supérieure à 21,3, et dans ce cas c’est l’intervalle [30,35) dont la fréquence cumulée absolue est 31. Maintenant que l’on connaît l’intervalle du décile, on appliquez la formule suivante pour trouver la valeur exacte du décile :
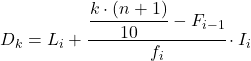
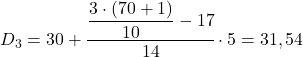
Il faut maintenant réappliquer la méthode pour obtenir le cinquième décile. Nous déterminons d’abord l’intervalle dans lequel il se trouve :
![]()
Le résultat 35 signifie qu’il est dans l’intervalle [35,40) mais pas parce qu’il y a un 35 dans l’expression de l’intervalle, mais parce que sa fréquence absolue accumulée (42) est la plus immédiatement élevée. Et une fois l’intervalle repéré, on applique la deuxième formule du procédé :
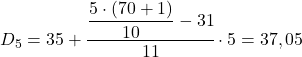
Enfin, on retrouve le huitième décile. Pour ce faire, on calcule d’abord son intervalle :
![]()
La fréquence absolue cumulée immédiatement au-dessus de 56,8 est de 58, donc la plage du huitième décile est de [40,45). Il suffit donc de déterminer la valeur exacte du décile :