Comment effectuer un test Z à deux proportions dans SAS
Un test z à deux proportions est utilisé pour déterminer s’il existe une différence statistiquement significative entre deux proportions de population.
Ce test utilise l’hypothèse nulle suivante :
- H 0 : μ 1 = μ 2 (les deux proportions de population sont égales)
L’hypothèse alternative peut être bilatérale, à gauche ou à droite :
- H 1 (bilatéral) : π 1 ≠ π 2 (les deux proportions de population ne sont pas égales)
- H 1 (à gauche) : π 1 < π 2 (la proportion de la population 1 est inférieure à la proportion de la population 2)
- H 1 (à droite) : π 1 > π 2 (la proportion de la population 1 est supérieure à la proportion de la population 2)
Nous utilisons la formule suivante pour calculer la statistique de test z :
z = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 )
où p 1 et p 2 sont les proportions de l’échantillon, n 1 et n 2 sont les tailles d’échantillon, et où p est la proportion totale regroupée calculée comme suit :
p = (p 1 n 1 + p 2 n 2 )/(n 1 + n 2 )
Si la valeur p qui correspond à la statistique de test z est inférieure au niveau de signification choisi (les choix courants sont 0,10, 0,05 et 0,01), vous pouvez alors rejeter l’hypothèse nulle.
L’exemple suivant montre comment effectuer un test z à deux proportions dans SAS.
Exemple : test Z à deux proportions dans SAS
Supposons que nous voulions savoir s’il existe une différence entre la proportion d’habitants qui soutiennent une certaine loi dans le comté A et la proportion qui soutient la loi dans le comté B.
Pour tester cela, nous collectons un échantillon aléatoire de 50 résidents de chaque comté et comptons combien soutiennent la loi.
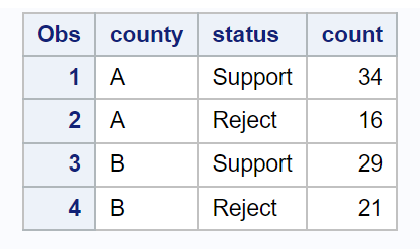
Le code suivant montre comment créer un ensemble de données résumant le nombre de résidents qui soutiennent la loi dans chaque comté :
/*create dataset*/ data my_data; input county $ status $ count; datalines; A Support 34 A Reject 16 B Support 29 B Reject 21 ; run; /*view dataset*/ proc print data=my_data;
Nous pouvons ensuite utiliser l’instruction PROC FREQ avec l’option Riskdiff (equal var = null) pour effectuer le test z à deux proportions :
/*perform two proportion z-test*/
proc freq data=my_data;
weight count;
tables county * status / riskdiff(equal var = null);
run;
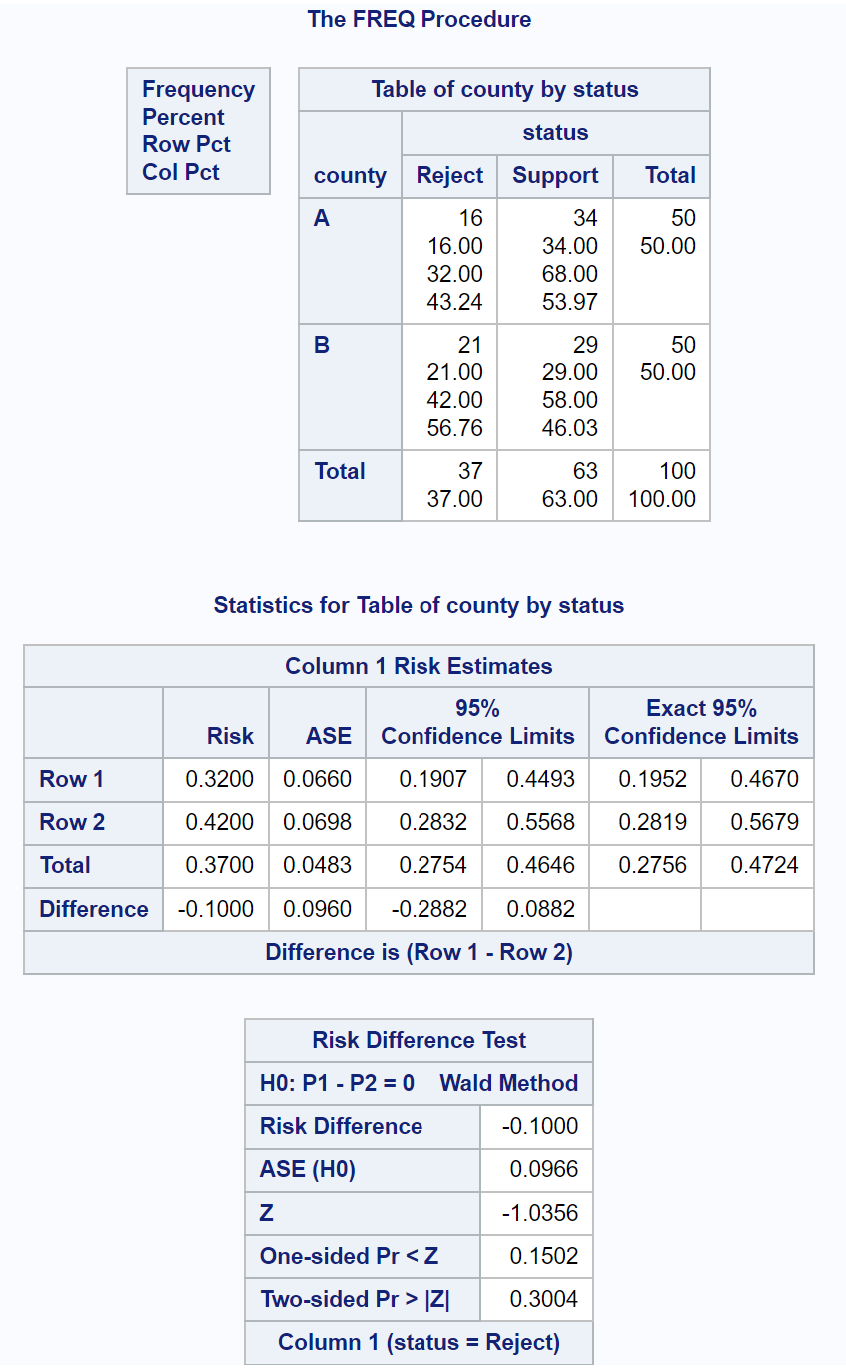
À partir du tableau Test de différence de risque dans le résultat, nous pouvons voir les informations suivantes :
- Statistique du test z : -1,0356
- Valeur p bilatérale : 0,3004
Ce test z particulier à deux proportions utilisait les hypothèses suivantes :
- H 0 : π 1 = π 2 (les deux proportions de population sont égales)
- H 1 : π 1 ≠ π 2 (les deux proportions de population ne sont pas égales)
Étant donné que la valeur p dans la sortie n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle.
Cela signifie que nous ne disposons pas de preuves suffisantes pour affirmer que la proportion de résidents qui soutiennent cette loi est différente entre les deux comtés.
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer d’autres tests statistiques courants dans SAS :
Comment effectuer un test t sur un échantillon dans SAS
Comment effectuer un test t à deux échantillons dans SAS
Comment effectuer un test t pour échantillons appariés dans SAS
