Comment créer un tracé de tiges et de feuilles avec des décimales

Un diagramme à tiges et à feuilles est un type de diagramme qui affiche les données en divisant chaque valeur d’un ensemble de données en une « tige » et une « feuille ».

Par exemple, supposons que nous ayons l’ensemble de données suivant :

Ensemble de données : 12, 14, 18, 22, 22, 23, 25, 25, 28, 45, 47, 48

Si nous définissons le premier chiffre de chaque valeur comme la « tige » et le deuxième chiffre comme la « feuille », nous pouvons alors créer le diagramme de tiges et de feuilles suivant :

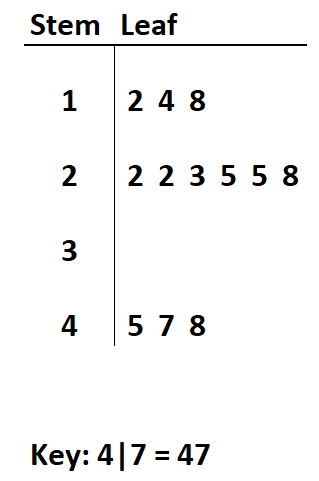
Bien que les tracés à tiges et à feuilles soient généralement utilisés avec des valeurs entières, ils peuvent également être utilisés pour des valeurs avec des décimales.

Les exemples suivants illustrent comment créer des tracés à tiges et à feuilles avec des décimales.

Exemple 1 : graphique de tiges et de feuilles avec une décimale

Supposons que nous ayons l’ensemble de données suivant :

Ensemble de données : 11.6, 12.2, 12.5, 12.6, 13.7, 13.8, 14.1, 15.2

Si nous définissons les chiffres devant la virgule comme tige et les chiffres après la virgule comme feuille, alors nous pouvons créer le diagramme de tige et de feuille suivant :

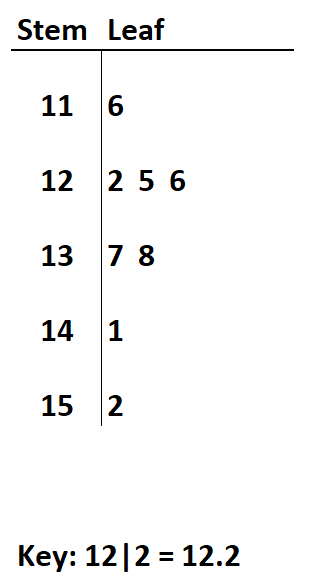
Lors de la création de ce tracé à tiges et à feuilles, il est important d’inclure une clé en bas afin que le lecteur sache comment interpréter les valeurs de la tige et de la feuille.

Exemple 2 : graphique de tiges et de feuilles avec plusieurs décimales

Supposons que nous ayons l’ensemble de données suivant :

Ensemble de données : 3.26, 3.28, 3.34, 3.38, 3.41, 3.42, 3.44, 3.59, 3.63

Si nous définissons l’entier et la première valeur après la décimale comme tige, et la deuxième valeur après la décimale comme feuille, alors nous pouvons créer le tracé de tiges et de feuilles suivant :

Encore une fois, la clé en bas du tracé nous indique comment interpréter les valeurs du tracé.

Exemple 3 : Interprétation d’un diagramme de tiges et de feuilles avec des décimales

Supposons que nous ayons le diagramme de tiges et de feuilles suivant avec décimales :

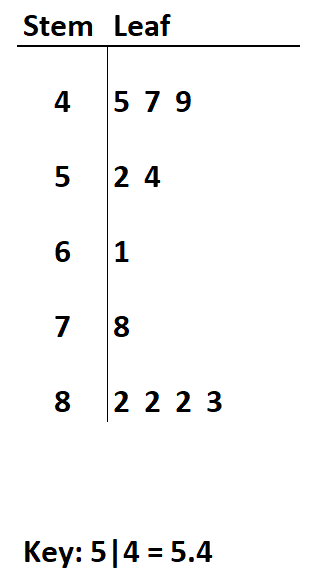
Question 1 : Quelle est la valeur maximale dans l’ensemble de données ?

La valeur maximale serait de 8,3 .

Question 2 : Quelle est la portée de l’ensemble de données ?

La plage de l’ensemble de données est la différence entre la plus grande et la plus petite valeur. Ainsi, la fourchette serait de 8,3 – 4,5 = 3,8 .

Question 3 : Quel est le mode de l’ensemble de données ?

Le mode est la valeur qui apparaît le plus souvent. Ce serait 8,2 .

Question 4 : Quelle est la médiane de l’ensemble de données ?

La médiane est définie comme la valeur « moyenne » de l’ensemble de données. Pour trouver cette valeur, nous pouvons écrire chacune des valeurs individuelles dans l’ensemble de données et trouver la valeur médiane :

Ensemble de données : 4.5, 4.7, 4.9, 5.2, 5.4, 6.1 , 7.8, 8.2, 8.2, 8.2, 8.3

La médiane est de 6,1 .

Ressources additionnelles

Une introduction aux parcelles de tiges et de feuilles
Une introduction aux tracés à tiges et à feuilles dos à dos
Générateur de parcelles de tiges et de feuilles
Comment créer un tracé à tiges et feuilles dans Excel