Diagramme en arbre

Cet article explique ce qu’est un diagramme en arbre et comment il est réalisé. Ainsi, vous trouverez des exemples d’arborescences, les avantages de ce type de diagramme et, en complément, un exercice résolu étape par étape.

Qu’est-ce qu’un arbre ?

Un diagramme en arbre , également appelé arbre de probabilité , est une représentation graphique de tous les résultats possibles d’une expérience ainsi que de leurs probabilités.

Ainsi, un diagramme arborescent est utilisé pour représenter graphiquement tous les résultats possibles dans un espace échantillon et calculer leurs probabilités.

Un diagramme arborescent est réalisé de telle manière que chaque résultat ( nœud ) se ramifie en de nouveaux résultats possibles ( branches ) jusqu’à atteindre les résultats finaux.

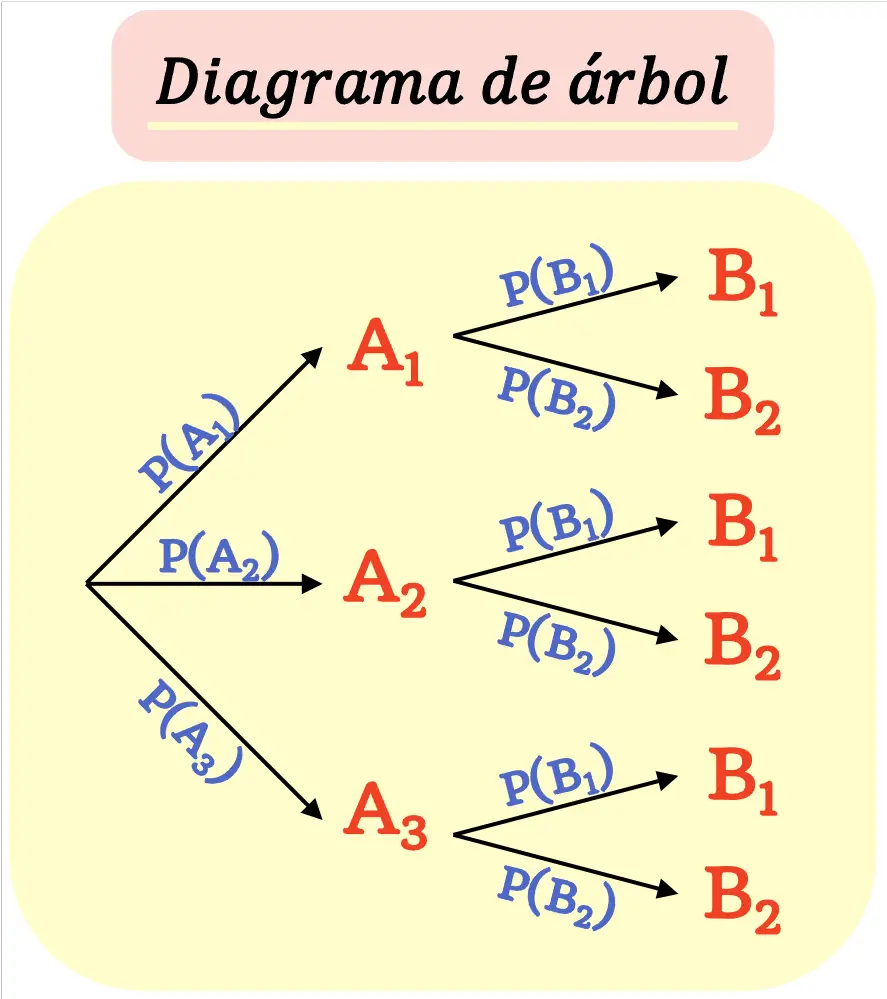
Il faut garder à l’esprit que la somme des probabilités de toutes les branches sortant d’un nœud doit être égale à 1.

Comment faire un diagramme en arbre

Pour créer un arbre, vous devez suivre les étapes suivantes :

1. La première étape pour créer un diagramme en arbre consiste à tracer une branche pour chaque résultat possible. Ce seront les branches de première génération.
2. Ensuite, la probabilité associée à chaque événement est ajoutée à sa branche correspondante.
3. La fin de chaque branche de première génération est un nœud à partir duquel doivent être représentées les branches des événements possibles suivants.
4. Comme dans les premières branches, il faut additionner les probabilités des événements représentés.
5. Répétez les étapes 3 et 4 jusqu’à atteindre les nœuds finaux, c’est-à-dire les fins possibles de l’expérience.

Notez que le nombre de branches dans un niveau ne doit pas nécessairement être égal au nombre de branches dans un niveau différent. De même, le nombre de branches qui résultent d’un résultat possible peut varier même au sein d’un même niveau.

Exemple d’arborescence

Maintenant que nous connaissons la définition et la théorie de la création d’un diagramme en arbre, examinons un exemple concret étape par étape pour mieux comprendre le concept.

• Construisez l’arbre de probabilité du tirage au sort de trois pièces indépendantes. Déterminez ensuite la probabilité d’obtenir face sur les trois lancers.

Au tirage au sort, il n’y a que deux résultats possibles, nous pouvons obtenir pile ou face. Par conséquent, la probabilité d’obtenir pile ou face en lançant une pièce est :

Une fois que nous connaissons les probabilités des résultats possibles, nous procédons à la représentation du diagramme en arbre.

Puisque les lancers de pièces sont indépendants, la probabilité d’obtenir pile ou face sera toujours la même pour chaque lancer. Par conséquent, pour construire l’arbre, deux branches (pile et queue) doivent être représentées avec la même probabilité pour chaque lancer effectué.

Et une fois que nous avons réalisé l’arbre, il ne nous reste plus qu’à déterminer la probabilité d’obtenir face au tirage à trois pièces.

Par conséquent, dans ce cas, nous devons multiplier toutes les probabilités d’obtenir face, car ce sont les probabilités du chemin qui nous mène au résultat souhaité.

Ainsi, la probabilité d’obtenir face aux trois lancers de pièces est calculée comme suit :

En bref, la probabilité d’obtenir face trois fois de suite est de 12,5 %.

Exercice d’arbre résolu

Dans un village il n’y a que 3 crèches : 60% des enfants vont à la crèche A, 30% à la crèche B et 10% à la crèche C. De plus, dans les trois crèches, 55 % des personnes sont des filles. Construisez l’arborescence et calculez les probabilités suivantes :

• Probabilité que lorsqu’un enfant est sélectionné au hasard, ce soit une fille de la garderie B.
• Probabilité que lorsqu’un enfant est sélectionné au hasard dans n’importe quelle garderie, ce soit un garçon.

À noter que si la proportion de filles dans toutes les garderies est de 55 %, le pourcentage de garçons se calcule en soustrayant simplement 1 moins 0,55 :

Maintenant que nous connaissons toutes les probabilités, nous pouvons réaliser l’arborescence avec les probabilités avec toutes les possibilités :

Ainsi, la probabilité de sélectionner au hasard une fille de la garderie B est calculée comme suit :

D’autre part, pour déterminer la probabilité de sélectionner un garçon dans n’importe quelle garderie, nous devons d’abord trouver la probabilité de choisir un garçon pour chaque garderie, puis les additionner :

Avantages de l’arborescence

De par les caractéristiques de l’arborescence, les avantages de ce type de graphe statistique sont les suivants :

• Les diagrammes arborescents sont très utiles pour prendre des décisions.
• La relation entre tous les résultats possibles peut être représentée graphiquement.
• Il est très pratique de trouver la cause première d’un problème.
• Facilite la résolution de problèmes de probabilités et de statistiques.
• Un diagramme en arbre permet d’organiser les idées et d’analyser la situation.