Diagramme matriciel (diagramme matriciel)

Dans cet article, nous expliquons ce qu’est un diagramme matriciel (ou diagramme matriciel) et à quoi il sert. Nous vous montrons également quels sont les différents types de diagrammes matriciels et un exemple de chaque type. Enfin, vous pourrez voir quels sont les avantages d’utiliser un diagramme matriciel.

Qu’est-ce qu’un diagramme matriciel (ou diagramme matriciel) ?

Un diagramme matriciel , également appelé diagramme matriciel ou matrice de relations , est un diagramme qui indique les relations entre différents éléments. Ainsi, un diagramme matriciel est utilisé pour montrer les liens entre les idées, les problèmes, les causes, les processus, les objectifs, etc. disposés en tableau.

En bref, le diagramme matriciel est un tableau dans lequel chaque ligne et chaque colonne correspond à un élément, de sorte que la case dans laquelle une ligne et une colonne se croisent représente la relation entre ces deux éléments.

Le diagramme matriciel est un outil souvent utilisé en gestion de projet, car il permet de montrer visuellement un grand nombre de relations entre différents éléments de manière résumée. En ce sens, les diagrammes matriciels aident à analyser les relations entre différents groupes d’informations.

De plus, le diagramme matriciel vous permet non seulement d’examiner les relations entre différents ensembles de données, mais il indique également l’importance des relations à l’aide de symboles. Dans la section suivante, vous pourrez voir plusieurs exemples de diagrammes matriciels et vous comprendrez mieux ce concept.

Types de diagramme matriciel

Les types de diagramme matriciel sont les suivants :

• Diagramme matriciel en forme de L.
• Diagramme matriciel en forme de T.
• Diagramme matriciel en forme de Y.
• Diagramme matriciel en forme de C.
• Diagramme matriciel en forme de X.

Chaque type de diagramme matriciel est expliqué ci-dessous et un exemple de chacun est présenté.

Diagramme matriciel en forme de L

Le diagramme matriciel en forme de L est un tableau simple dans lequel les lignes représentent un ensemble de données et les colonnes représentent un autre ensemble de données. Ainsi, chaque cellule du tableau indique la relation entre les éléments de la ligne et de la colonne correspondantes.

Les éléments représentés d’un diagramme matriciel de type L forment un L inversé, c’est pourquoi il reçoit ce nom.

La relation entre les différents éléments peut être définie essentiellement par des chiffres, du texte ou des symboles. Ce type de diagramme matriciel est le plus simple et le plus utilisé de tous.

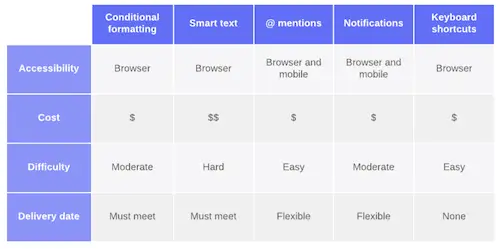
Diagramme matriciel en forme de T

Le diagramme matriciel en forme de T est essentiellement constitué de deux diagrammes matriciels en forme de L reliés par une seule liste. Cette matrice permet de comparer une liste (la rangée du milieu du T) avec deux autres groupes de données.

Ce type de diagramme de relations est particulièrement utile lorsque vous devez comparer deux groupes liés à une liste parent (mais pas l’un à l’autre).

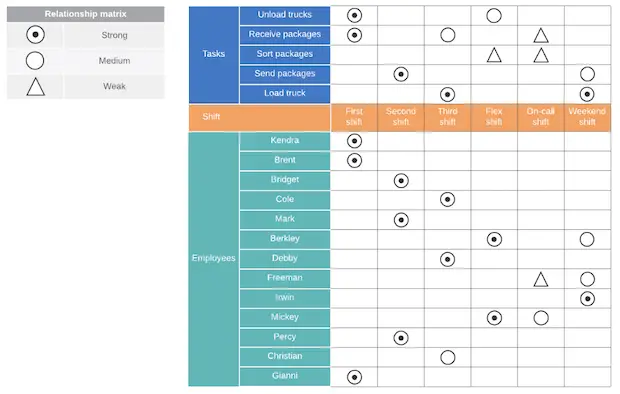
Diagramme matriciel en forme de Y

Le diagramme matriciel en forme de Y relie trois groupes d’éléments qui sont tous liés les uns aux autres. Ces relations sont représentées dans un diagramme circulaire.

Par conséquent, ce type de diagramme matriciel doit être utilisé lorsque vous devez comparer trois groupes liés et qu’ils sont tous liés les uns aux autres.

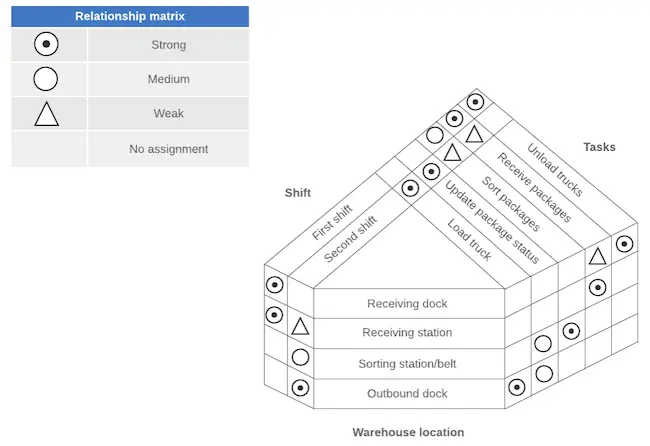
Diagramme matriciel en forme de C

Le diagramme matriciel en forme de C est similaire au diagramme matriciel en forme de Y dans le sens où il est également utile pour comparer trois ensembles de données. Cependant, le diagramme matriciel en forme de C relie les trois groupes simultanément dans un diagramme cubique tridimensionnel.

Le diagramme matriciel en forme de C doit donc être utilisé lorsque vous devez comparer trois groupes simultanément, par exemple des personnes, des produits et des processus dans une usine.

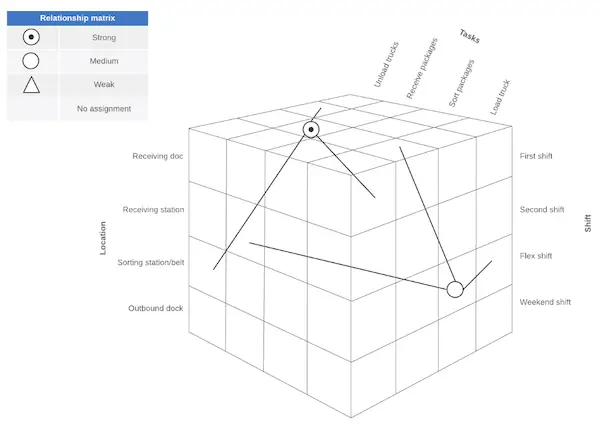
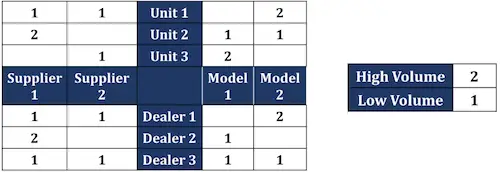
Diagramme matriciel en forme de X

Le diagramme matriciel en X permet de comparer deux paires de listes complémentaires. Il est similaire au diagramme matriciel T, mais étend le diagramme T pour inclure un ensemble de données supplémentaire.

Le résultat est un diagramme avec des axes X et Y formant une forme de croix ou « X » qui compare quatre groupes de données totales. Dans cette matrice de relations, chaque axe est lié aux groupes qui lui sont immédiatement adjacents, mais pas au groupe qui lui fait face.

Par conséquent, vous devez utiliser ce type de diagramme matriciel lorsque vous devez comparer quatre groupes d’éléments différents.

Comment faire un diagramme matriciel

Pour réaliser un diagramme matriciel, les étapes suivantes doivent être suivies :

1. Définissez l’objectif : avant de réaliser le diagramme matriciel, vous devez être clair sur ce que vous espérez obtenir à partir du diagramme. Cela vous permettra de mieux concevoir le graphique et de choisir le bon type de diagramme matriciel.
2. Collecter des données : pour réaliser le diagramme matriciel vous devez identifier les différents groupes de données et leurs éléments, puis vous devez déterminer quelle est la relation entre les éléments des différents groupes.
3. Choisir le bon type de diagramme matriciel – En fonction de vos ensembles de données et de l’objectif de votre projet, choisissez le type de diagramme matriciel qui correspond le mieux à vos besoins. Dans la section précédente, nous avons expliqué quand chaque type de diagramme matriciel doit être utilisé.
4. Décidez de la notation du diagramme : Vous devez décider comment vous indiquerez la relation entre les différents éléments. Vous pouvez utiliser des chiffres, des symboles, des mots ou des phrases en fonction de votre objectif. N’oubliez pas que si vous utilisez des symboles dans les cellules du graphique, vous devez ajouter une légende expliquant leur signification.
5. Analyser et ajouter des informations – Analyse chaque cellule et les éléments qui y sont connectés, puis utilise la méthode de notation choisie pour enregistrer des informations sur la relation entre ces éléments. Complétez ainsi tout le diagramme.
6. Interpréter le schéma matriciel : étudier le schéma matriciel obtenu et tirer les conclusions des connexions entre les éléments. De même, réfléchissez aux constats par rapport à l’objectif initialement énoncé.

Avantages du diagramme matriciel

Le diagramme matriciel présente les avantages suivants par rapport aux autres diagrammes :

• Le diagramme matriciel permet de simplifier des relations complexes, permettant ainsi de mieux les analyser.
• En lien avec l’avantage précédent, le diagramme matriciel facilite la prise de décision, car en comprenant tous les éléments qui participent au projet et quelle est la relation entre eux, de meilleures décisions peuvent être prises.
• Il s’agit d’un type de diagramme polyvalent, car il peut être utilisé dans une grande variété de cas.
• En fin de compte, les diagrammes matriciels sont très utiles pour l’amélioration des processus et la résolution de problèmes, car ils fournissent une structure pour les données et un moyen systématique d’évaluer la manière dont les groupes de données interagissent.

Quand utiliser un diagramme matriciel

L’utilisation du diagramme matriciel est particulièrement utile dans les situations suivantes :

• Déterminez les causes d’un problème.
• Allouer les ressources en fonction des compétences et des exigences.
• Comparez différents ensembles de données.
• Identifiez les opportunités d’amélioration.
• Analyser le respect des exigences.