Test Dickey-Fuller augmenté dans R (avec exemple)

Une série temporelle est dite « stationnaire » si elle n’a pas de tendance, présente une variance constante dans le temps et possède une structure d’autocorrélation constante dans le temps.

Une façon de tester si une série chronologique est stationnaire consiste à effectuer un test de Dickey-Fuller augmenté , qui utilise les hypothèses nulles et alternatives suivantes :

H ₀ : La série temporelle est non stationnaire. En d’autres termes, sa structure dépend du temps et sa variation n’est pas constante dans le temps.

H _A : La série temporelle est stationnaire.

Si la valeur p du test est inférieure à un certain niveau de signification (par exemple α = 0,05), nous pouvons alors rejeter l’hypothèse nulle et conclure que la série chronologique est stationnaire.

L’exemple étape par étape suivant montre comment effectuer un test Dickey-Fuller augmenté dans R pour une série chronologique donnée.

Exemple : test Dickey-Fuller augmenté dans R

Supposons que nous ayons les données de séries chronologiques suivantes dans R :

data <- c(3, 4, 4, 5, 6, 7, 6, 6, 7, 8, 9, 12, 10)

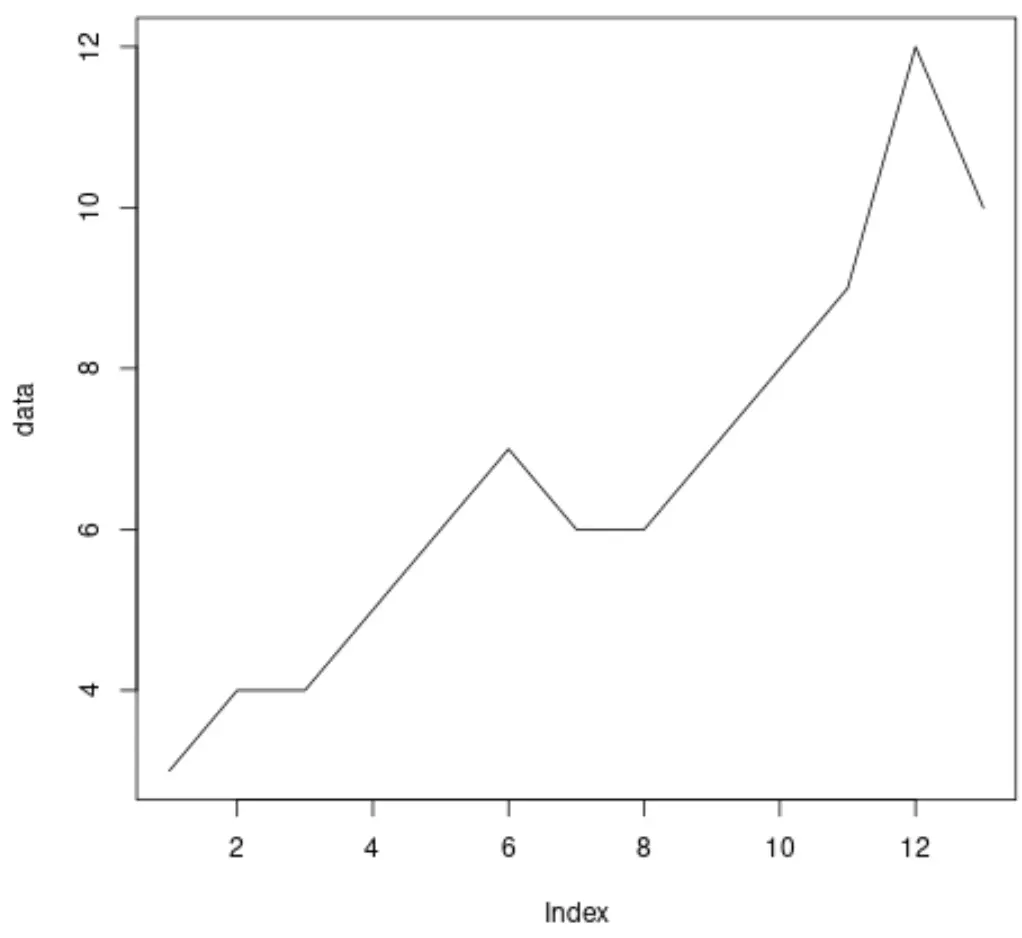
Avant d’effectuer un test Dickey-Fuller augmenté sur les données, nous pouvons créer un tracé rapide pour visualiser les données :

plot(data, type='l')

Pour effectuer un test Dickey-Fuller augmenté, nous pouvons utiliser la fonction adf.test() de la bibliothèque tseries .

Le code suivant montre comment utiliser cette fonction :

library(tseries)

#perform augmented Dickey-Fuller test 
adf.test(data)

	Augmented Dickey-Fuller Test

data:  data
Dickey-Fuller = -2.2048, Lag order = 2, p-value = 0.4943
alternative hypothesis: stationary

Voici comment interpréter les valeurs les plus importantes du résultat :

• Statistique de test : -2,2048
• Valeur P : 0,4943

Puisque la valeur p n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle.

Cela signifie que la série chronologique n’est pas stationnaire. En d’autres termes, sa structure dépend du temps et sa variation n’est pas constante dans le temps.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans R :

Comment effectuer un test de tendance Mann-Kendall dans R
Comment tracer une série chronologique dans R
Comment réduire la tendance des données