Distribution bêta

Par Pr Amélia Rodriguez août 4, 2023 Probabilité 0 commentaire

Cet article explique ce qu’est la distribution bêta et à quoi elle sert. De même, vous pourrez voir le graphique de la distribution bêta et les propriétés de ce type de distribution de probabilité.

Quelle est la distribution bêta ?

La distribution bêta est une distribution de probabilité définie sur l’intervalle (0,1) et paramétrée par deux paramètres positifs : α et β. Autrement dit, les valeurs de la distribution bêta dépendent des paramètres α et β.

Par conséquent, la principale caractéristique de la distribution bêta est que sa forme peut être contrôlée par les paramètres α et β. De plus, la distribution bêta est utilisée pour définir des variables aléatoires dont la valeur est comprise entre 0 et 1.

Il existe plusieurs notations pour indiquer qu’une variable aléatoire continue est régie par une distribution bêta, les plus courantes sont :

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex]X\sim Beta(\alpha,\beta)\\[2ex]X\sim \beta_{\alpha,\beta}\end{array}$

En statistiques, la distribution bêta a des applications très variées. Par exemple, la distribution bêta est utilisée pour étudier les variations de pourcentages dans différents échantillons. De même, en gestion de projet, la distribution bêta est utilisée pour réaliser une analyse Pert.

Tracé de la distribution bêta

Compte tenu de la définition de la distribution bêta, la fonction de densité et la fonction de distribution de probabilité de la distribution bêta sont représentées graphiquement ci-dessous.

Ci-dessous vous pouvez voir comment le graphique de la fonction densité de la distribution bêta varie en fonction des paramètres α et β.

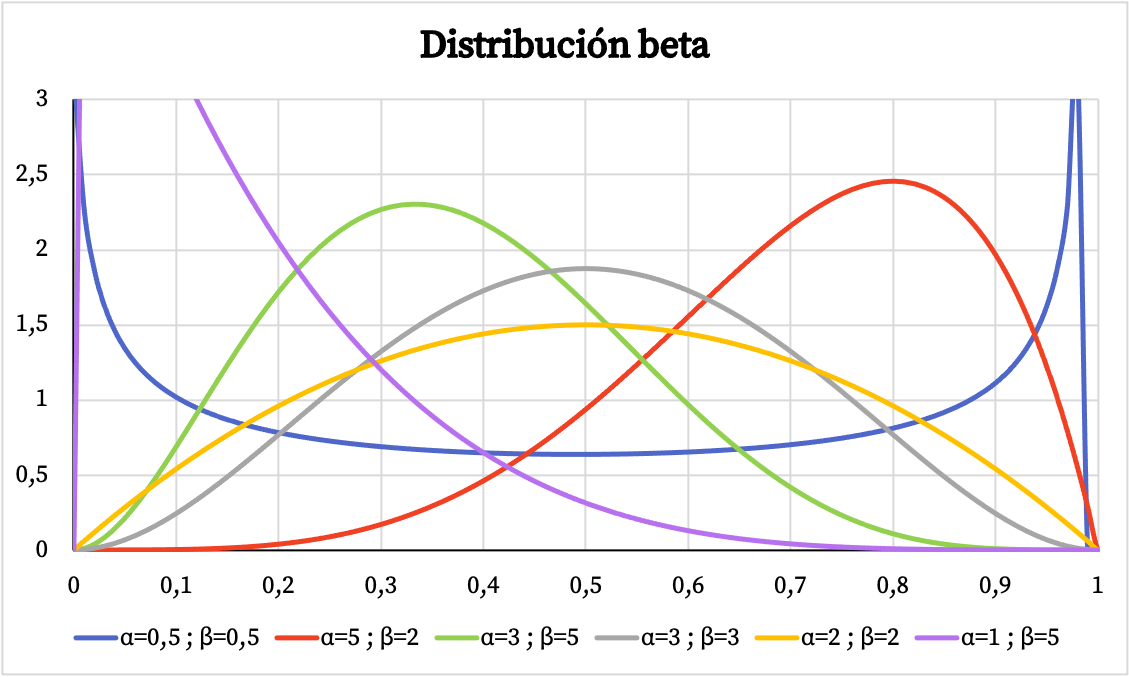
De même, vous pouvez voir ci-dessous la représentation graphique de la probabilité cumulée de la distribution bêta en fonction des paramètres α et β.

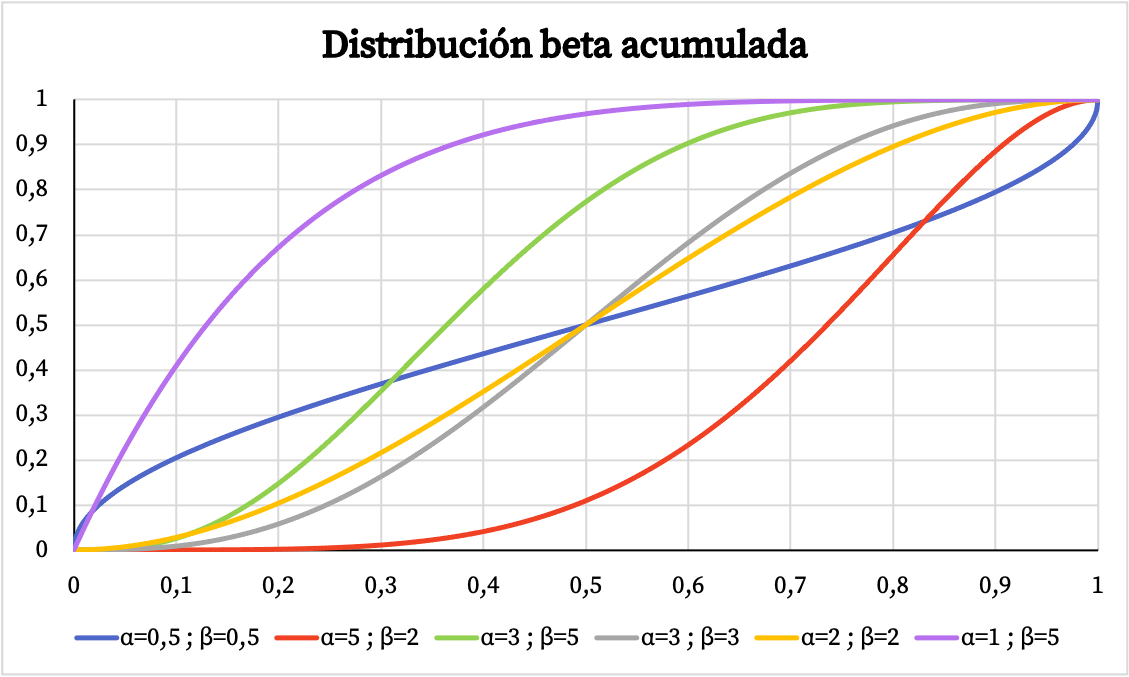
graphique de la distribution bêta cumulée

Caractéristiques de la distribution bêta

Dans cette section, nous verrons quelles sont les caractéristiques les plus importantes de la distribution bêta.

Les paramètres α et β de la distribution bêta sont des nombres réels et positifs.

$\begin{array}{c}\alpha >0\\[2ex] \beta >0\end{array}$

Le domaine de la distribution bêta va de 0 à 1, les deux extrêmes ne sont pas inclus.

$x\in (0,1)$

La moyenne de la distribution bêta est égale à alpha divisé par la somme alpha plus bêta.

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] E[X]=\cfrac{\alpha}{\alpha+\beta}\end{array}$

La variance de la distribution bêta peut être calculée à l’aide de la formule suivante :

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] Var(X)=\cfrac{\alpha\cdot \beta}{(\alpha+\beta+1)\cdot (\alpha+\beta)^2}\end{array}$

Pour les valeurs d’alpha et de bêta supérieures à 1, le mode de distribution bêta peut être facilement trouvé avec l’expression suivante :

$Mo=\cfrac{\alpha-1}{\alpha+\beta-2}\qquad \alpha,\beta>1$

La fonction de densité de la distribution bêta est la suivante :

$\displaystyle P[X=x]=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}$

Où B(α,β) est la fonction bêta, qui est définie comme :

$\displaystyle B(\alpha,\beta)=\int_0^1x^{\alpha-1}(1-x)^{\beta-1}dx$

La fonction de probabilité cumulée de la distribution bêta est la suivante :

$\displaystyle P[X\leq x]=\frac{B(x;\alpha,\beta)}{B(\alpha,\beta)}$

Où B(x;α,β) est la fonction bêta incomplète, définie comme :

$\displaystyle B(x;\,a,b) = \int_0^x t^{a-1}\,(1-t)^{b-1}\,dt$

Si X est une variable définie par une distribution bêta, alors 1-X est une variable définie par une distribution bêta dont les paramètres alpha et bêta sont respectivement les paramètres bêta et alpha de la distribution bêta d’origine.

$X\sim B(\alpha,\beta) \ \color{orange}\bm{\longrightarrow}\color{black} \ 1-X\sim B(\beta,\alpha)$

Si les paramètres alpha et bêta de la distribution bêta sont tous deux égaux à 1, alors la distribution est équivalente à une distribution uniforme des paramètres 0 et 1.

$X\sim B(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim U(0,1)$

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus

Quelle est la distribution bêta ?

Tracé de la distribution bêta

Caractéristiques de la distribution bêta

à propos de l'auteur

Pr Amélia Rodriguez

Ajouter un commentaire