Distribution binomiale

Par Pr Amélia Rodriguez août 3, 2023 Probabilité 0 commentaire

Cet article explique ce qu’est la distribution binomiale dans les statistiques et à quoi elle sert. Vous trouverez donc la définition de la distribution binomiale, des exemples de distributions binomiales et les propriétés de ce type de distribution de probabilité. De plus, vous pourrez calculer n’importe quelle probabilité de la distribution binomiale avec un calculateur en ligne.

Quelle est la distribution binomiale ?

La distribution binomiale est une distribution de probabilité qui compte le nombre de réussites lors de la réalisation d’une série d’expériences indépendantes et dichotomiques avec une probabilité de réussite constante.

Autrement dit, la distribution binomiale est une distribution qui décrit le nombre de résultats réussis d’une séquence d’essais de Bernoulli.

N’oubliez pas qu’un essai Bernoulli est une expérience qui a deux résultats possibles : le « succès » et l’« échec ». Par conséquent, si la probabilité de « succès » est p , la probabilité d’« échec » est q=1-p .

En général, le nombre total d’expériences réalisées est défini avec le paramètre n , tandis que p est la probabilité de réussite de chaque expérience. Ainsi, une variable aléatoire qui suit une distribution binomiale s’écrit comme suit :

$X\sim\text{Bin}(n,p)$

Notez que dans une distribution binomiale, la même expérience exacte est répétée n fois et les expériences sont indépendantes les unes des autres, donc la probabilité de succès de chaque expérience est la même (p) .

La distribution binomiale peut également être appelée distribution binomiale .

Exemples de distribution binomiale

Une fois que nous aurons vu la définition de la distribution binomiale, nous allons voir plusieurs exemples de variables qui suivent ce type de distribution pour mieux comprendre le concept.

Nombre de fois où « face » apparaît lorsque vous lancez une pièce de monnaie 25 fois.
Nombre de tirs effectués par un basketteur lorsqu’il tire 60 fois vers le panier depuis le même endroit.
Nombre de fois où nous obtenons le chiffre 6 en lançant un dé 30 fois.
Nombre de réussites sur un total de 50 étudiants qui passent un examen.
Nombre d’unités défectueuses dans un échantillon de 100 produits.

Formule de distribution binomiale

Étant donné les paramètres x, n, p, la fonction de probabilité de la distribution binomiale est définie comme le nombre combinatoire de n en x fois p ^x fois (1-p) ^nx .

Par conséquent, la formule pour calculer la probabilité d’une distribution binomiale est la suivante :

👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer la probabilité d’une variable qui suit la distribution binomiale.

D’autre part, la probabilité cumulée de la distribution binomiale est calculée en additionnant les probabilités du nombre de cas de réussite en question et toutes les probabilités précédentes. Ainsi, la formule pour calculer une probabilité cumulée d’une distribution binomiale est la suivante :

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Exercice résolu sur la distribution binomiale

On lance une pièce de monnaie 10 fois, quelle est la probabilité d’obtenir 6 faces ?

La variable de ce problème suit une distribution binomiale car tous les lancements sont indépendants les uns des autres et ont de plus la même probabilité de succès.

Concrètement, la probabilité de réussite est de 50 %, puisqu’un seul des deux résultats possibles est considéré comme une réussite.

$p=\cfrac{1}{2}=0,5$

Par conséquent, la distribution pour cet exercice est un binôme avec un total de 10 expériences et une probabilité de 0,5.

$X\sim\text{Bin}(10 ; 0,5)$

Ainsi, pour déterminer la probabilité d’obtenir six faces, nous devons appliquer la formule de la distribution binomiale.

$\begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}$

Ainsi, la probabilité d’obtenir exactement six faces en lançant une pièce dix fois est de 20,51 %.

Caractéristiques de la distribution binomiale

La distribution binomiale répond aux caractéristiques suivantes :

La distribution binomiale est définie avec deux paramètres : n est le nombre total d’expériences de Bernoulli et, d’autre part, p est la probabilité de succès de chaque expérience de Bernoulli.

$\begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}$

La moyenne d’une distribution binomiale est égale au produit du nombre total d’expériences multiplié par la probabilité de succès de chaque expérience. Par conséquent, pour calculer la moyenne d’une distribution binomiale, il faut multiplier n par p .

$E[X]=n\cdot p$

La variance d’une distribution binomiale équivaut au nombre total d’essais multiplié par la probabilité de succès et la probabilité d’échec.

$Var(X)=n\cdot p\cdot (1-p)$

La formule de la fonction de probabilité de la distribution binomiale est la suivante :

$\displaystyle P[X=x]&=\begin{pmatrix}n\\ x\end{pmatrix}p^x(1-p)^{n-x}$

De même, la formule de la fonction de distribution cumulative de la distribution binomiale est la suivante :

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

La somme de deux distributions binomiales indépendantes avec la même probabilité équivaut à une distribution binomiale avec la même valeur de probabilité p et n étant la somme du nombre total d’essais des deux distributions.

$\begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}$

$\displaystyle P[Z=z]=\begin{pmatrix}n+m\\z\end{pmatrix}p^z(1-p)^{n+m-z}$

La distribution de Bernoulli est un cas particulier de distribution binomiale dans laquelle n=1 , c’est-à-dire qu’une seule expérience est réalisée.

$X\sim\text{Bin}(1,p) \quad \color{orange}\bm{\longrightarrow}\color{black}\quad X\sim\text{Bernoulli}(p)$

_Si _X 1 , _X ₂ ,…, X _k sont des variables aléatoires indépendantes telles que

$\displaystyle\sum_{i=1}^k X_i\sim \text{Bin}\left(\sum_{i=1}^k n_i,p\right)$

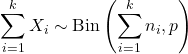
Calculateur de distribution binomiale

Entrez les valeurs des paramètres p, n et x de la distribution binomiale dans la calculatrice suivante pour calculer la probabilité. Vous devez sélectionner la probabilité que vous souhaitez calculer et saisir les nombres en utilisant le point comme séparateur décimal, par exemple 0,1667.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus