Comment utiliser la distribution binomiale dans Google Sheets
La distribution binomiale en statistique décrit la probabilité d’obtenir k succès dans n essais lorsque la probabilité de succès dans une seule expérience est p .
Pour calculer les probabilités de distribution binomiale dans Google Sheets, nous pouvons utiliser la fonction BINOMDIST , qui utilise la syntaxe de base suivante :
BINOMDIST(k, n, p, cumulatif)
où:
- k : Nombre de réussites
- n : Nombre d’essais
- p : Probabilité de succès sur un essai donné
- cumulative : s’il faut calculer une probabilité cumulée (la valeur par défaut est FALSE)
Les exemples suivants montrent comment utiliser cette fonction dans la pratique.
Exemple 1 : Probabilité d’exactement k succès
Ty réussit 60 % de ses tentatives de lancer franc. S’il réussit 12 lancers francs, quelle est la probabilité qu’il en réalise exactement 10 ?
Pour répondre à cette question, nous pouvons utiliser la formule suivante dans Google Sheets :
=BINOMDIST(10, 12, 0.6, FALSE)
La capture d’écran suivante montre comment utiliser cette formule en pratique :
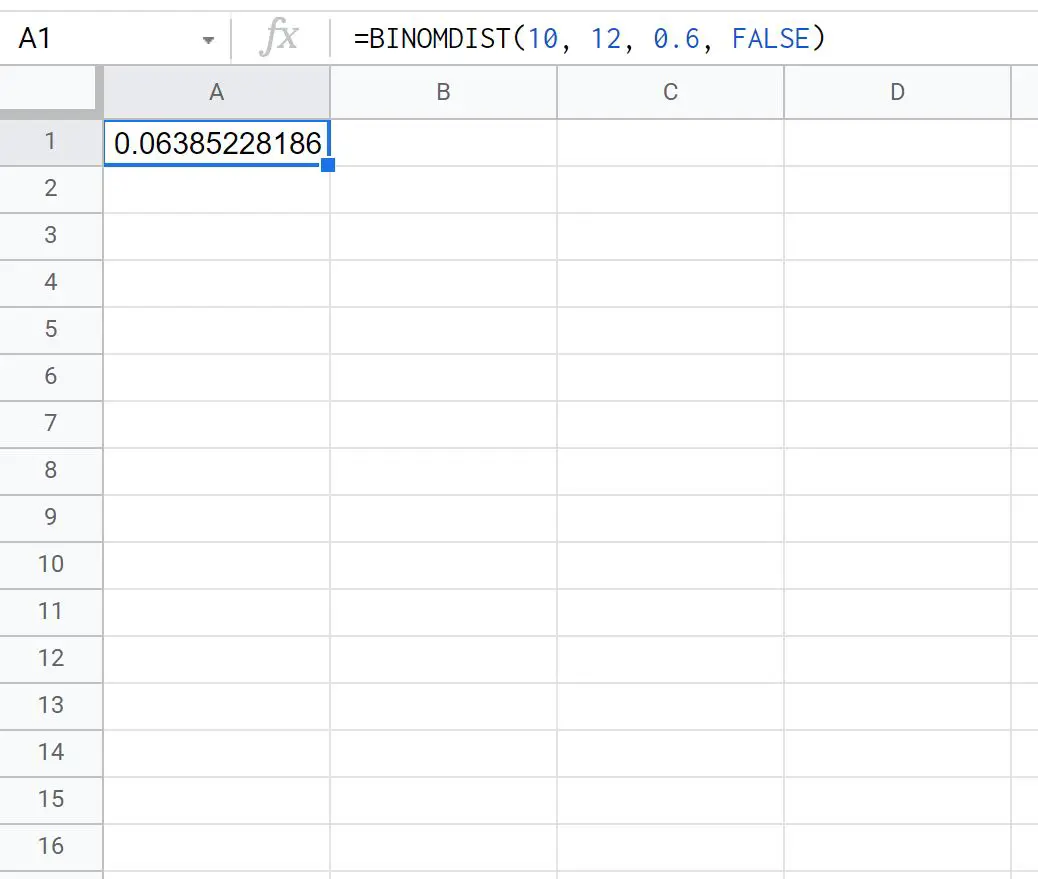
La probabilité que Ty réalise exactement 10 tentatives de lancer franc sur 12 est de 0,0639 .
Exemple 2 : Probabilité de succès inférieurs à k
Ty réussit 60 % de ses tentatives de lancer franc. S’il réussit 12 lancers francs, quelle est la probabilité qu’il en réalise moins de 10 ?
Pour répondre à cette question, nous pouvons utiliser la formule suivante dans Google Sheets :
=BINOMDIST(9, 12, 0.6, TRUE)
La capture d’écran suivante montre comment utiliser cette formule en pratique :
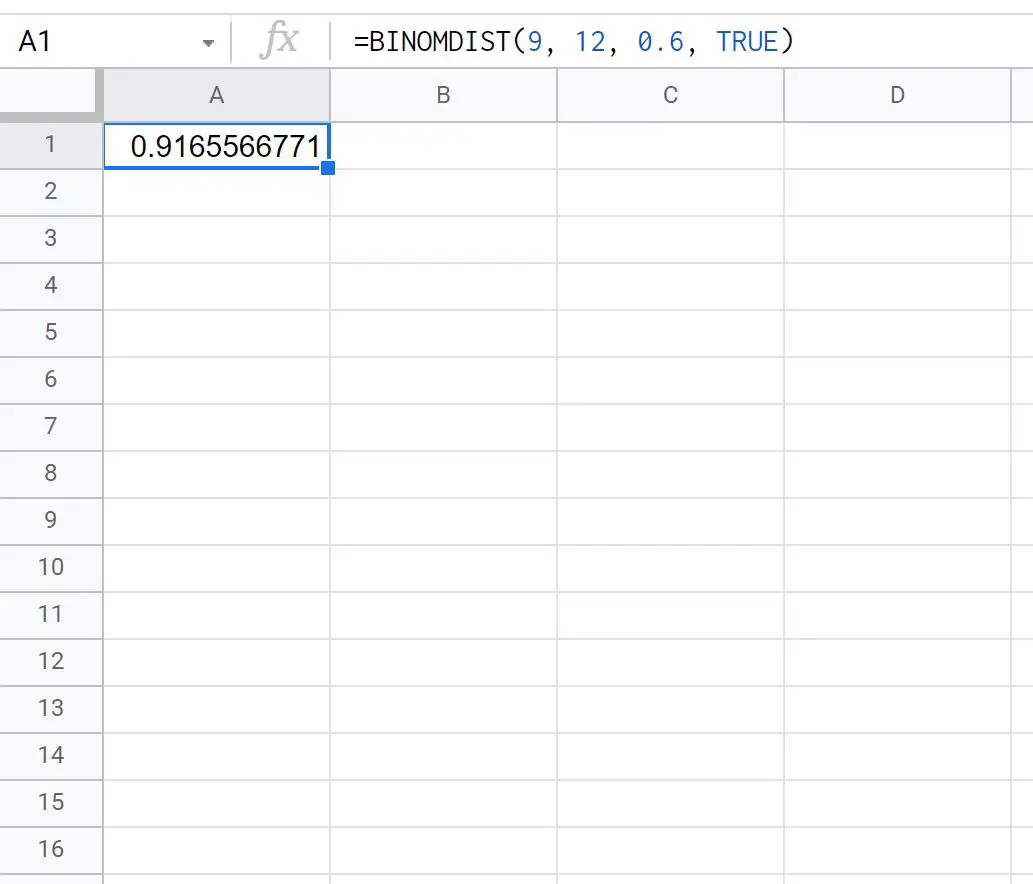
La probabilité que Ty réalise moins de 10 tentatives de lancer franc sur 12 est de 0,9166 .
Exemple 3 : Probabilité inférieure ou égale à k succès
Ty réussit 60 % de ses tentatives de lancer franc. S’il réussit 12 lancers francs, quelle est la probabilité qu’il en réalise un inférieur ou égal à 10 ?
Pour répondre à cette question, nous pouvons utiliser la formule suivante dans Google Sheets :
=BINOMDIST(10, 12, 0.6, TRUE)
La capture d’écran suivante montre comment utiliser cette formule en pratique :
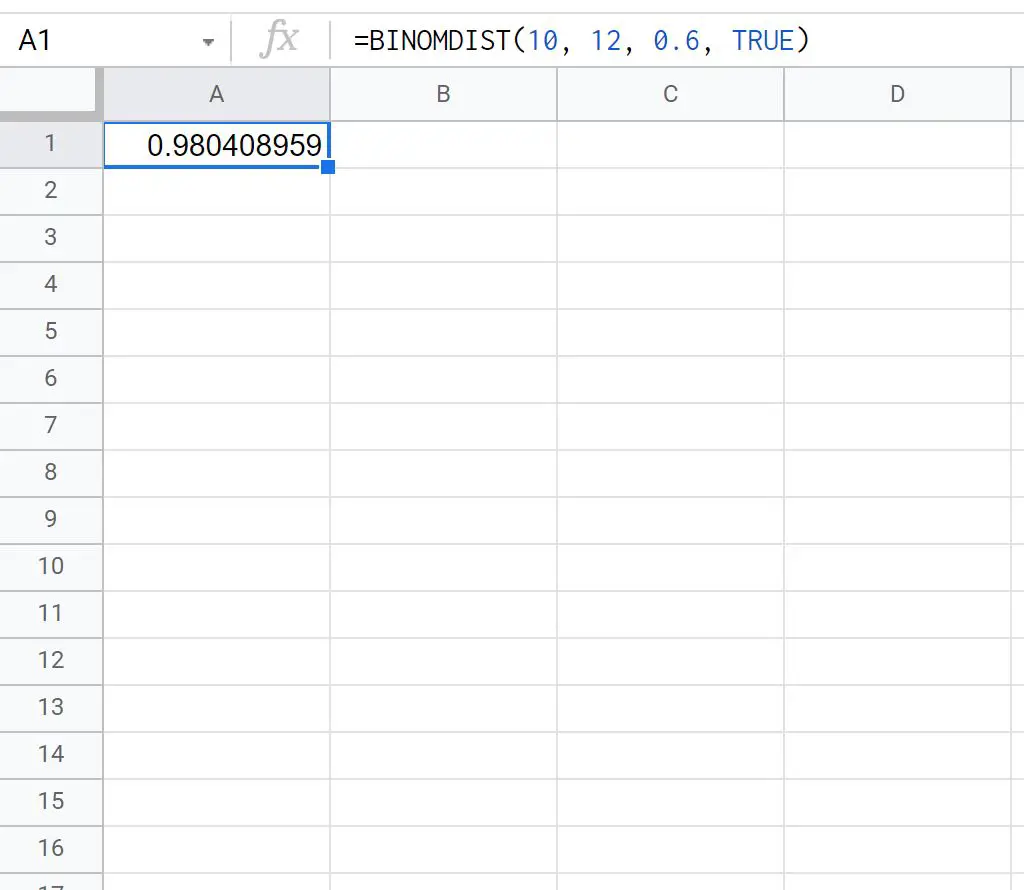
La probabilité que Ty réalise moins ou égale à 10 tentatives de lancer franc sur 12 est de 0,9166 .
Exemple 4 : Probabilité de succès plus importants
Ty réussit 60 % de ses tentatives de lancer franc. S’il réussit 12 lancers francs, quelle est la probabilité qu’il en réalise plus de 10 ?
Pour répondre à cette question, nous pouvons utiliser la formule suivante dans Google Sheets :
=1-BINOMDIST(10, 12, 0.6, TRUE)
La capture d’écran suivante montre comment utiliser cette formule en pratique :
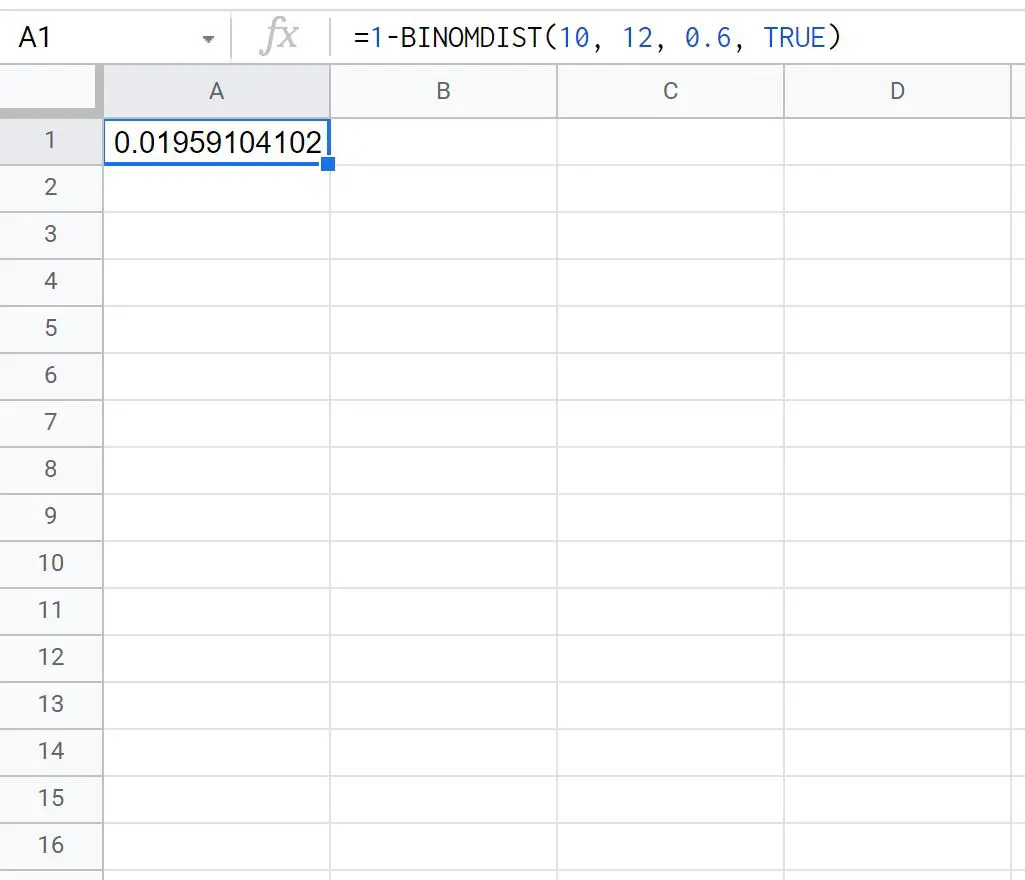
La probabilité que Ty réalise plus de 10 tentatives de lancer franc sur 12 est de 0,0196 .
Exemple 5 : Probabilité de succès supérieur ou égal à k
Ty réussit 60 % de ses tentatives de lancer franc. S’il réussit 12 lancers francs, quelle est la probabilité qu’il réussisse un total supérieur ou égal à 10 ?
Pour répondre à cette question, nous pouvons utiliser la formule suivante dans Google Sheets :
=1-BINOMDIST(9, 12, 0.6, TRUE)
La capture d’écran suivante montre comment utiliser cette formule en pratique :
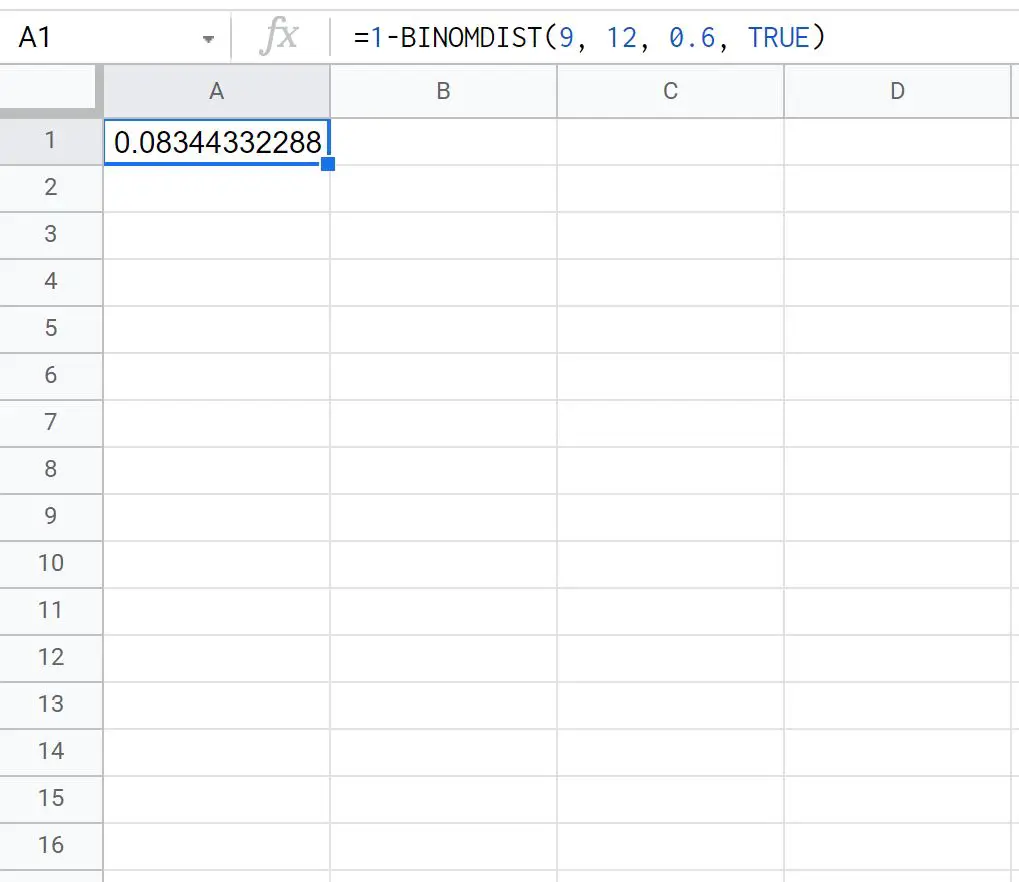
La probabilité que Ty réalise un nombre supérieur ou égal à 10 tentatives de lancer franc sur 12 est de 0,0834 .
Bonus : vous pouvez utiliser le calculateur de distribution binomiale pour calculer automatiquement les probabilités binomiales pour toutes les valeurs de n , k et p .
Ressources additionnelles
Les didacticiels suivants fournissent des informations supplémentaires sur la distribution binomiale :
Une introduction à la distribution binomiale
Les trois hypothèses de la distribution binomiale
5 exemples concrets de la distribution binomiale
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus