Distribution d’échantillonnage

Par Pr Amélia Rodriguez août 3, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est la distribution d’échantillonnage dans les statistiques et à quoi elle sert. Ainsi, vous trouverez la signification d’une distribution d’échantillonnage, un exemple concret de distribution d’échantillonnage et, en plus, les formules pour les types de distributions d’échantillonnage les plus courants.

Quelle est la distribution d’échantillonnage ?

La distribution d’échantillonnage , ou distribution d’échantillonnage , est la distribution qui résulte de la prise en compte de tous les échantillons possibles d’une population. Autrement dit, la distribution d’échantillonnage est la distribution obtenue en calculant un paramètre d’échantillonnage de tous les échantillons possibles d’une population.

Par exemple, si nous extrayons tous les échantillons possibles d’une population statistique et calculons la moyenne de chaque échantillon, l’ensemble des moyennes d’échantillon forme une distribution d’échantillonnage. Plus précisément, puisque le paramètre calculé est la moyenne arithmétique, il s’agit de la distribution d’échantillonnage de la moyenne.

En statistique, la distribution d’échantillonnage est utilisée pour calculer la probabilité d’approcher la valeur du paramètre de population lors de l’étude d’un seul échantillon. De même, la distribution d’échantillonnage nous permet d’estimer l’erreur d’échantillonnage pour une taille d’échantillon donnée.

Exemple de distribution d’échantillonnage

Maintenant que nous connaissons la définition de la distribution d’échantillonnage, regardons un exemple simple pour bien comprendre le concept.

Dans une boîte, nous mettons trois boules et chacune porte un numéro écrit de un à trois, de sorte qu’une boule porte le numéro 1, une autre boule porte le numéro 2 et la dernière boule porte le numéro 3. Pour un échantillon de taille n =2 , calcule les probabilités de la distribution d’échantillonnage de la moyenne si les échantillons avec remise sont sélectionnés.

Les échantillons sont sélectionnés avec remplacement, c’est-à-dire que la bille ramassée pour sélectionner le premier élément de l’échantillon est remise dans la boîte et peut être à nouveau sélectionnée lors de la deuxième extraction. Par conséquent, tous les échantillons possibles de la population sont :

1,1 1,2 1,3
2,1 2,2 2,3
3,1 3,2 3,3

Ainsi, nous calculons la moyenne arithmétique de chaque échantillon possible :

$(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{11}=\cfrac{1+1}{2}=1$

$(1,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{12}=\cfrac{1+2}{2}=1,5$

$(1,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{13}=\cfrac{1+3}{2}=2$

$(2,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{21}=\cfrac{2+1}{2}=1,5$

$(2,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{22}=\cfrac{2+2}{2}=2$

$(2,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{23}=\cfrac{2+3}{2}=2,5$

$(3,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{31}=\cfrac{3+1}{2}=2$

$(3,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{32}=\cfrac{3+2}{2}=2,5$

$(3,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{33}=\cfrac{3+3}{2}=3$

Par conséquent, les probabilités d’obtenir chaque valeur de la moyenne de l’échantillon lors de la sélection d’un échantillon aléatoire de la population sont les suivantes :

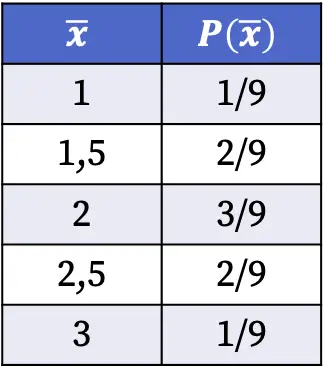
exemple de tableau de distribution d'échantillonnage

Les probabilités de la distribution d’échantillonnage indiquées dans le tableau ci-dessus ont été calculées en divisant le nombre d’échantillons ayant ladite valeur moyenne par le nombre total de cas possibles. Par exemple : la moyenne de l’échantillon est de 1,5 dans deux cas sur neuf possibles, donc P(1,5)=2/9.

Types de distributions d’échantillonnage

Les distributions d’échantillonnage (ou distributions d’échantillonnage) peuvent être classées en fonction du paramètre d’échantillonnage à partir duquel elles ont été obtenues. Ainsi, les types de distributions les plus courants sont les suivants :

Distribution d’échantillonnage de la moyenne : c’est la distribution d’échantillonnage qui résulte du calcul de la moyenne arithmétique de chaque échantillon.
Distribution d’échantillonnage de proportion : C’est la distribution d’échantillonnage obtenue en calculant la proportion de tous les échantillons.
Distribution d’échantillonnage de la variance : c’est la distribution d’échantillonnage qui forme l’ensemble de toutes les variances de l’échantillon.
Distribution d’échantillonnage de la différence des moyennes : est la distribution d’échantillonnage qui résulte du calcul de la différence entre les moyennes de tous les échantillons possibles de deux populations différentes.
Distribution d’échantillonnage de la différence de proportions : est la distribution d’échantillonnage obtenue en soustrayant toutes les proportions d’échantillonnage possibles de deux populations.

Chaque type de distribution d’échantillonnage est expliqué plus en détail ci-dessous.

Distribution d’échantillonnage de la moyenne

Étant donné une population qui suit une distribution de probabilité normale de moyenne

$\mu$ et écart type $\sigma$ et des échantillons de taille en sont extraits $n$ , la distribution d’échantillonnage de la moyenne sera également définie par une distribution normale ayant les caractéristiques suivantes :

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

Où

$\mu_{\overline{x}}$ est la moyenne de la distribution d’échantillonnage de la moyenne et $\sigma_{\overline{x}}$ est son écart type. En outre, $\cfrac{\sigma}{\sqrt{n}}$ est l’erreur type de la distribution d’échantillonnage.

Remarque : Si la population ne suit pas une distribution normale mais que la taille de l’échantillon est grande (n>30), la distribution d’échantillonnage de la moyenne peut également être rapprochée de la distribution normale ci-dessus par le théorème central limite.

Par conséquent, puisque la distribution d’échantillonnage de la moyenne suit une distribution normale, la formule pour calculer toute probabilité liée à la moyenne d’un échantillon est la suivante :

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

Où:

$\overline{x}$ est la moyenne de l’échantillon.
$\mu$ C’est la moyenne de la population.
$s$ est l’écart type de la population.
$n$ est la taille de l’échantillon.
$Z$ est une variable définie par la distribution normale standard N(0,1).

➤ Voir : Exercice résolu sur la distribution d’échantillonnage de la moyenne

Distribution d’échantillonnage de la proportion

En fait, lorsque nous étudions une proportion d’un échantillon, nous analysons les cas de réussite. Par conséquent, la variable aléatoire de l’étude suit une distribution de probabilité binomiale.

D’après le théorème central limite, pour les grandes tailles (n>30) on peut rapprocher une distribution binomiale d’une distribution normale. Par conséquent, la distribution d’échantillonnage de la proportion se rapproche d’une distribution normale avec les paramètres suivants :

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

Où

$p$ est la probabilité de succès et $q$ est la probabilité d’échec $q=1-p$ .

Remarque : Une distribution binomiale ne peut être approchée d’une distribution normale que si

$n>30$ , $np\ge 5$ et $nq\ge 5$ .

Par conséquent, puisque la distribution d’échantillonnage de la proportion peut être approchée d’une distribution normale, la formule pour calculer toute probabilité liée à la proportion d’un échantillon est la suivante :

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

Où:

$\widehat{p}$ est la proportion de l’échantillon.
$p$ est la proportion de la population.
$q$ est la probabilité d’échec de la population, $q=1-p$ .
$n$ est la taille de l’échantillon.
$Z$ est une variable définie par la distribution normale standard N(0,1).

➤ Voir : Exercice résolu sur la distribution d’échantillonnage de la proportion

Distribution d’échantillonnage de la variance

La distribution d’échantillonnage de la variance est définie par la distribution de probabilité du chi carré. Par conséquent, la formule pour la statistique de la distribution d’échantillonnage de la variance est la suivante :

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Où:

$\chi^2$ est la statistique de la distribution d’échantillonnage de la variance, qui suit une distribution du chi carré.
$n$ est la taille de l’échantillon.
$s^2$ est la variance de l’échantillon.
$\sigma^2$ est la variance de la population.

➤ Voir : Exercice résolu sur la distribution d’échantillonnage de la variance

Distribution d’échantillonnage de la différence de moyennes

Si la taille de l’échantillon est suffisamment grande (n ₁ ≥30 et n ₂ ≥30), la distribution d’échantillonnage de la différence moyenne suit une distribution normale. Plus précisément, les paramètres de ladite distribution sont calculés comme suit :

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Remarque : Si les deux populations sont des distributions normales, alors la distribution d’échantillonnage de la différence de moyenne suit une distribution normale quelle que soit la taille des échantillons.

Par conséquent, puisque la distribution d’échantillonnage de la différence de moyennes est définie par une distribution normale, la formule pour calculer la statistique de la distribution d’échantillonnage de la différence de moyennes est la suivante :

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Où:

$\overline{x_i}$ est la moyenne de l’échantillon i.
$\mu_i$ est la moyenne de la population i.
$\sigma_i$ est l’écart type de la population i.
$n_i$ est la taille de l’échantillon i.
$Z$ est une variable définie par la distribution normale standard N(0,1).

Notez que les échantillons provenant de différentes populations peuvent avoir des tailles d’échantillon différentes.

➤ Voir : Exercice résolu sur la distribution d’échantillonnage de la différence de moyennes

Répartition d’échantillonnage de la différence de proportions

Les échantillons sélectionnés pour la distribution d’échantillonnage de la différence de proportions sont définis par des distributions binomiales, car pour des raisons pratiques, une proportion est un rapport entre les cas de réussite et le nombre total d’observations.

Cependant, en raison du théorème central limite, les distributions binomiales peuvent être approchées des distributions de probabilité normales. Par conséquent, la distribution d’échantillonnage de la différence de proportions peut être approchée d’une distribution normale avec les caractéristiques suivantes :

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

Remarque : La distribution d’échantillonnage de la différence de proportions ne peut être approchée d’une distribution normale que si

$n_1\geq30$ , $n_2\geq 30$ , $n_1p_1\geq5$ , $n_2p_2\geq5$ , $n_1q_1\geq5$ et $n_2q_2\geq5$ .

Par conséquent, puisque la distribution d’échantillonnage de la différence de proportions peut être approchée d’une distribution normale, la formule pour calculer la statistique de la distribution d’échantillonnage de la différence de proportions est la suivante :

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

Où:

$\widehat{p_i}$ est la proportion d’échantillon i.
$p_i$ est la proportion de population i.
$q_i$ est la probabilité d’échec de la population i, $q_i=1-p_i$ .
$n_i$ est la taille de l’échantillon i.
$Z$ est une variable définie par la distribution normale standard N(0,1).

➤ Voir : Exercice résolu sur la distribution d’échantillonnage de la différence de proportions

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus