Comment calculer les distributions d’échantillonnage dans Excel

Une distribution d’échantillonnage est une distribution de probabilité d’une certaine statistique basée sur de nombreux échantillons aléatoires provenant d’une seule population .

Ce didacticiel explique comment effectuer les opérations suivantes avec des distributions d’échantillonnage dans Excel :

• Générez une distribution d’échantillonnage.
• Visualisez la distribution d’échantillonnage.
• Calculez la moyenne et l’écart type de la distribution d’échantillonnage.
• Calculer les probabilités concernant la distribution d’échantillonnage.

Générer une distribution d’échantillonnage dans Excel

Supposons que nous souhaitions générer une distribution d’échantillonnage composée de 1 000 échantillons dans laquelle chaque taille d’échantillon est de 20 et provient d’une distribution normale avec une moyenne de 5,3 et un écart type de 9 .

Nous pouvons facilement le faire en tapant la formule suivante dans la cellule A2 de notre feuille de calcul :

=NORM.INV(RAND(), 5.3, 9)

Nous pouvons ensuite survoler le coin inférieur droit de la cellule jusqu’à ce qu’un petit + apparaisse et faire glisser la formule vers la droite de 20 cellules et vers le bas de 1 000 cellules :

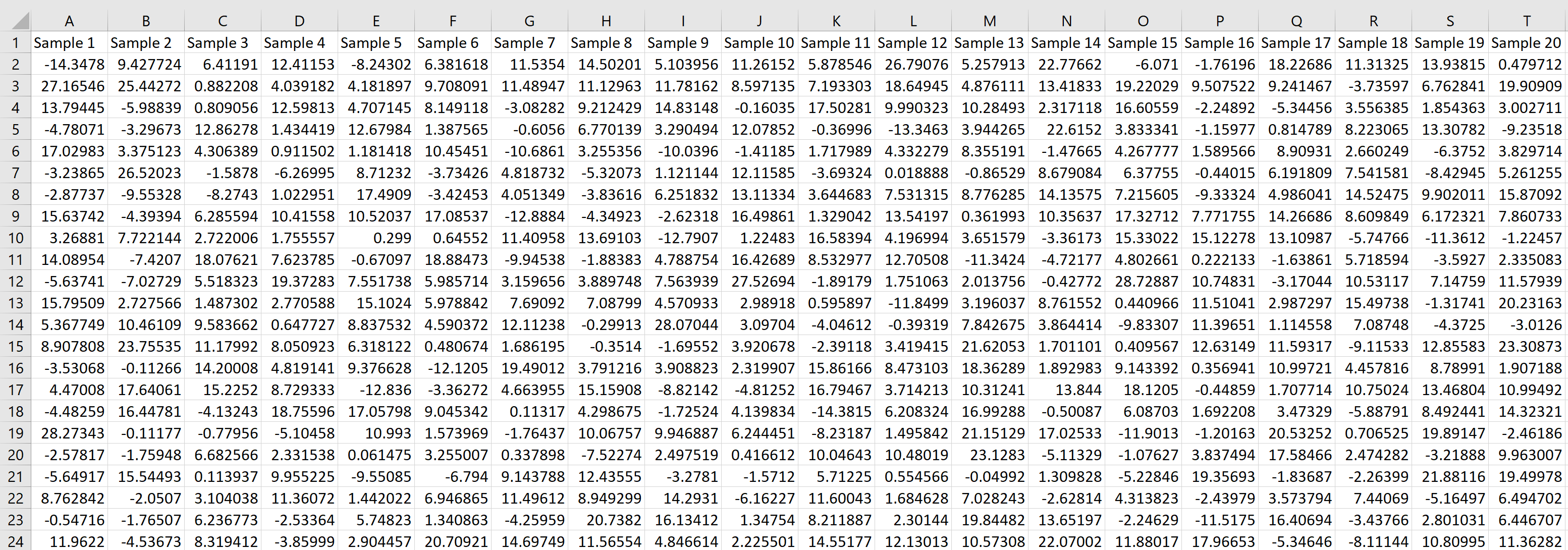
Chaque ligne représente un échantillon de taille 20 dans lequel chaque valeur provient d’une distribution normale avec une moyenne de 5,3 et un écart type de 9.

Trouver la moyenne et l’écart type

Pour trouver la moyenne et l’écart type de cette distribution d’échantillonnage des moyennes d’échantillon, nous pouvons d’abord trouver la moyenne de chaque échantillon en tapant la formule suivante dans la cellule U2 de notre feuille de calcul :

=AVERAGE(A2:T2)

Nous pouvons ensuite survoler le coin inférieur droit de la cellule jusqu’à ce qu’un petit + apparaisse et double-cliquer pour copier cette formule dans toutes les autres cellules de la colonne U :

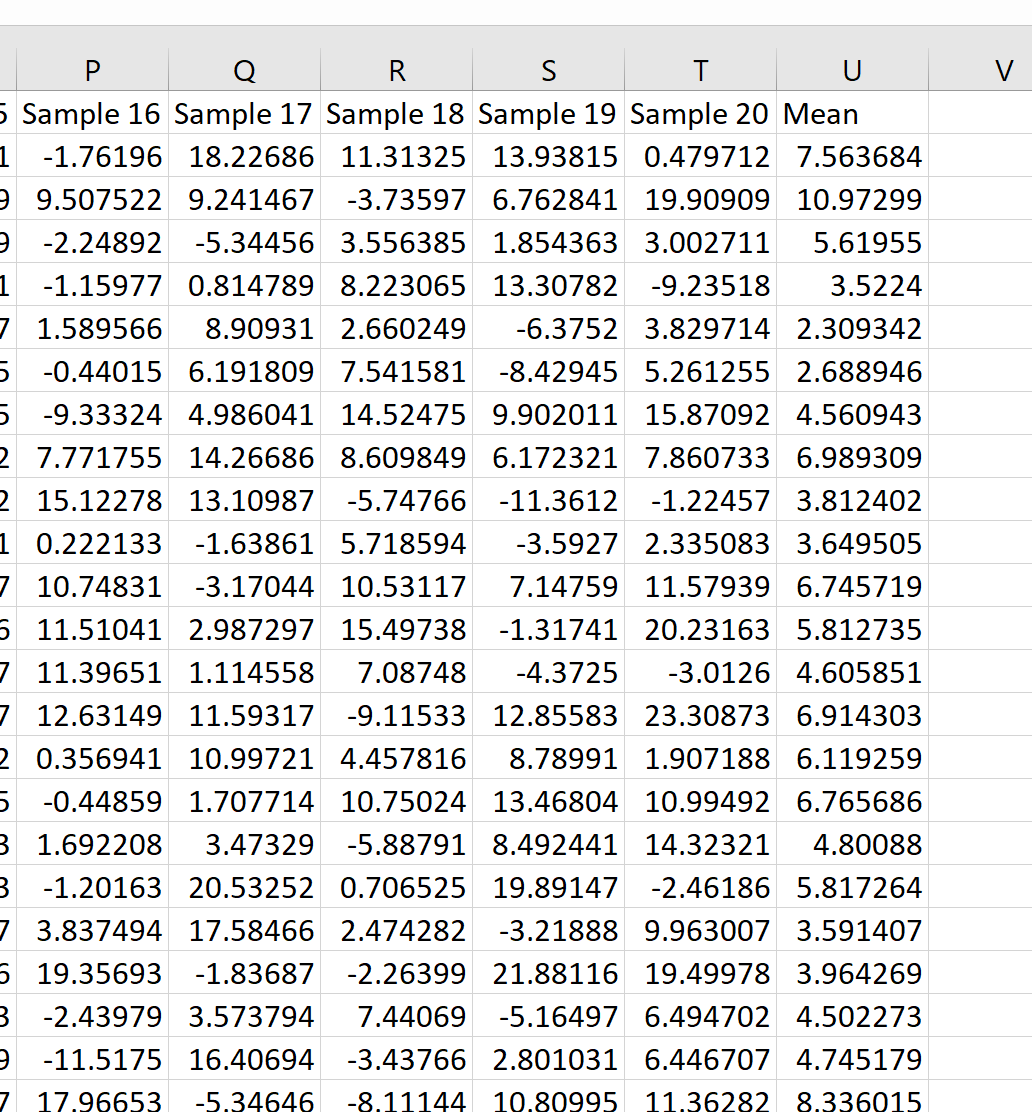
Nous pouvons voir que le premier échantillon avait une moyenne de 7,563684, le deuxième échantillon avait une moyenne de 10,97299, et ainsi de suite.

Nous pouvons ensuite utiliser les formules suivantes pour calculer la moyenne et l’écart type des moyennes de l’échantillon :

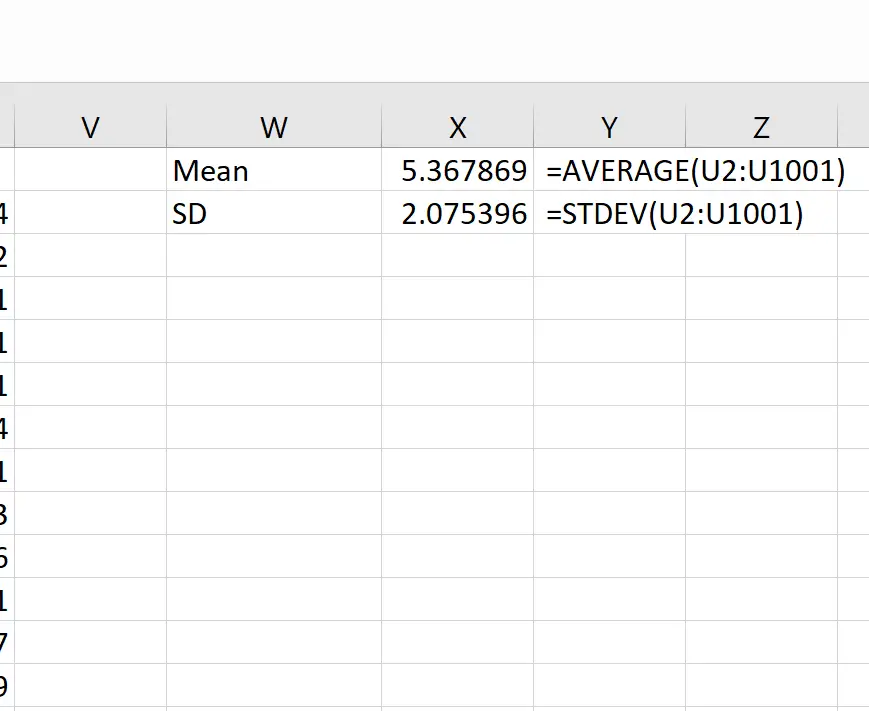
Théoriquement, la moyenne de la distribution d’échantillonnage devrait être de 5,3. Nous pouvons voir que la moyenne d’échantillonnage réelle dans cet exemple est de 5,367869 , ce qui est proche de 5,3.

Et théoriquement, l’écart type de la distribution d’échantillonnage devrait être égal à s/√n, ce qui serait 9 / √20 = 2,012. Nous pouvons voir que l’écart type réel de la distribution d’échantillonnage est de 2,075396 , ce qui est proche de 2,012.

Visualisez la distribution d’échantillonnage

Nous pouvons également créer un histogramme simple pour visualiser la distribution d’échantillonnage des moyennes d’échantillon.

Pour ce faire, mettez simplement en surbrillance toutes les moyennes de l’échantillon dans la colonne U, cliquez sur l’onglet Insérer , puis cliquez sur l’option Histogramme sous la section Graphiques .

Cela donne l’histogramme suivant :

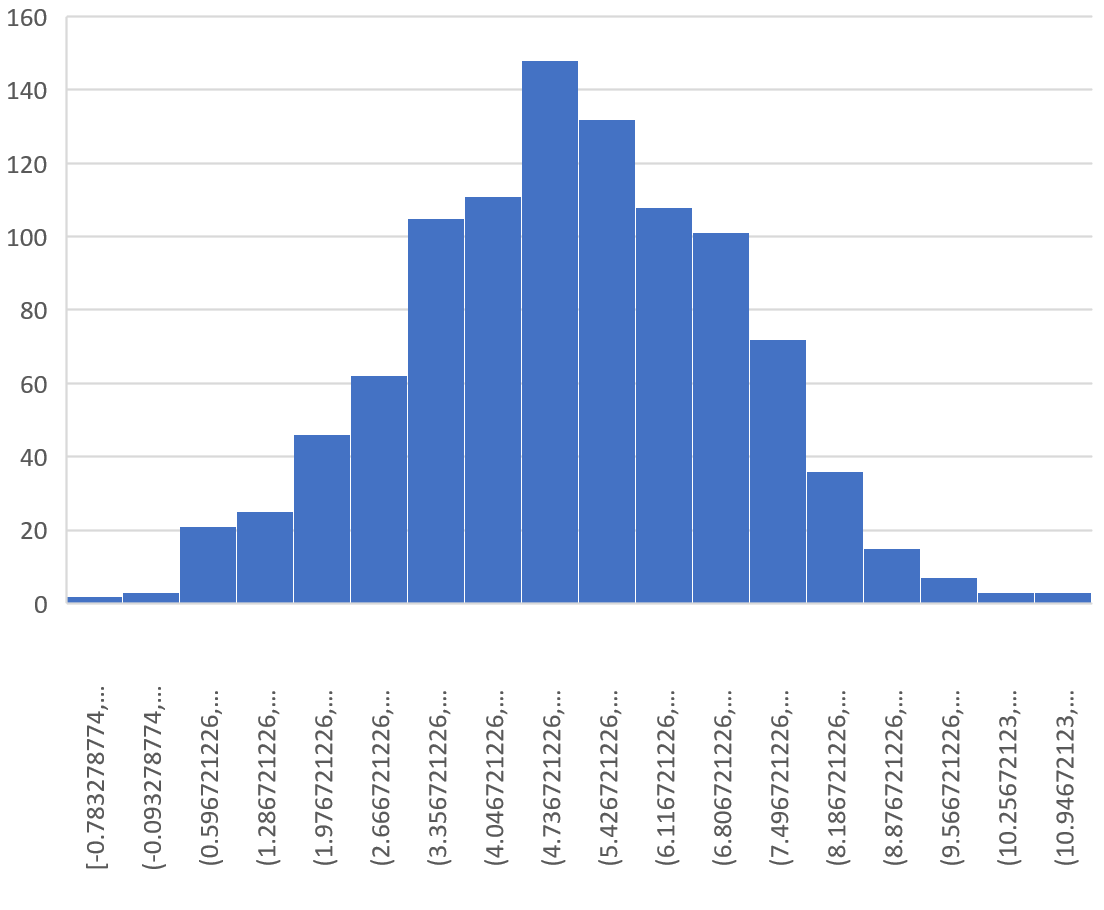
On peut voir que la distribution d’échantillonnage est en forme de cloche avec un pic proche de la valeur 5.

Cependant, à partir des queues de la distribution, nous pouvons voir que certains échantillons avaient des moyennes supérieures à 10 et d’autres des moyennes inférieures à 0.

Calculer les probabilités

Nous pouvons également calculer la probabilité d’obtenir une certaine valeur pour la moyenne d’un échantillon, en fonction de la moyenne de la population, de l’écart type de la population et de la taille de l’échantillon.

Par exemple, nous pouvons utiliser la formule suivante pour trouver la probabilité que la moyenne de l’échantillon soit inférieure ou égale à 6, étant donné que la moyenne de la population est de 5,3, l’écart type de la population est de 9 et la taille de l’échantillon est :

=COUNTIF(U2:U1001, "<=6")/COUNT(U2:U1001)

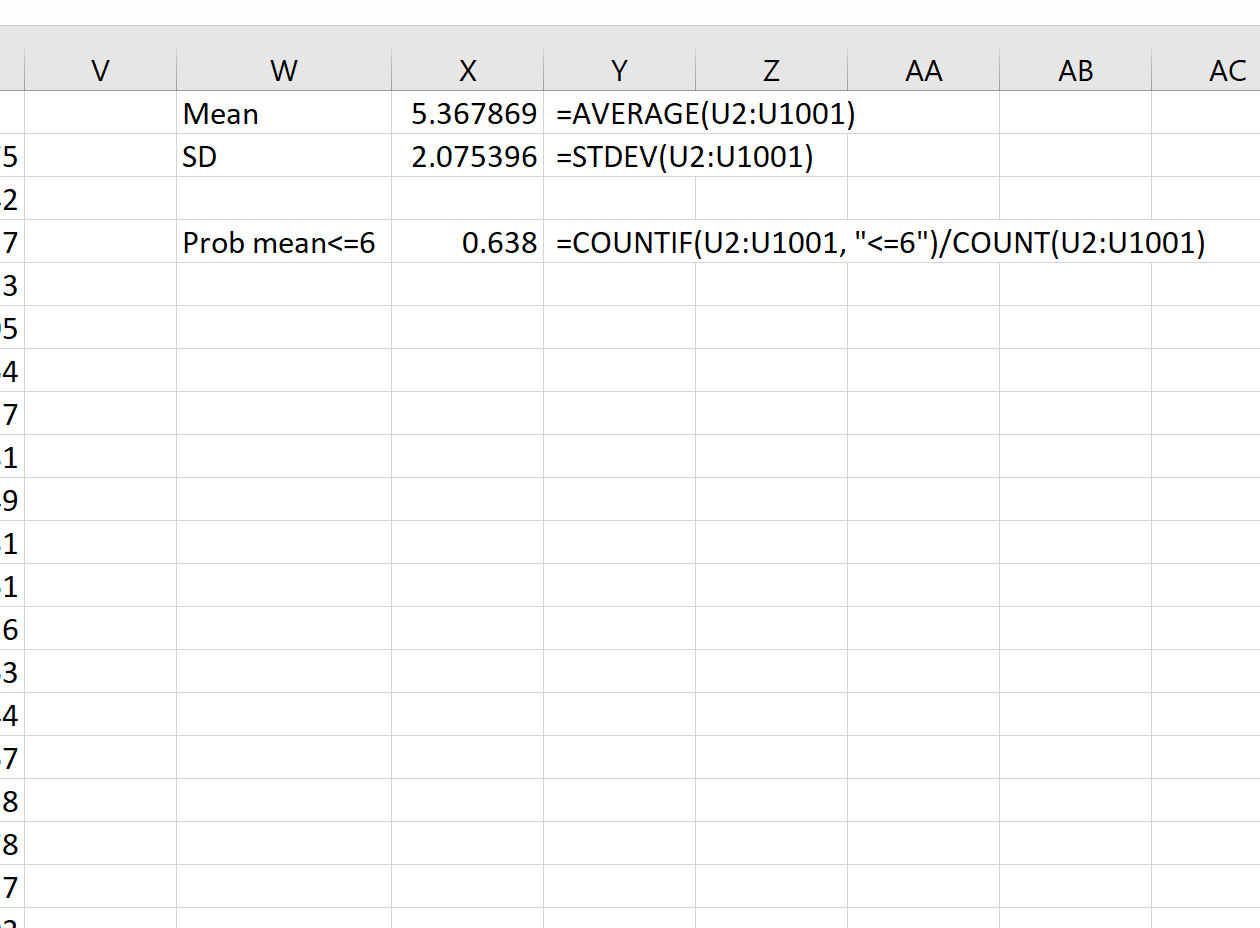
On voit que la probabilité que la moyenne de l’échantillon soit inférieure ou égale à 6 est de 0,638.

Ceci est très proche de la probabilité calculée par le Sampling Distribution Calculator :

Ressources additionnelles

Une introduction aux distributions d’échantillonnage
Calculateur de distribution d’échantillonnage
Une introduction au théorème central limite