Qu’est-ce qu’une distribution de probabilité conjointe ?

Un tableau de fréquences bidirectionnel est un tableau qui affiche les fréquences (ou « comptes ») pour deux variables catégorielles.

Par exemple, le tableau à double entrée suivant montre les résultats d’une enquête qui a demandé à 100 personnes quel sport elles préféraient : le baseball, le basket-ball ou le football.

Les lignes affichent le sexe du répondant et les colonnes indiquent le sport qu’il a choisi :

Dans cet exemple, il y a deux variables : Sports et Sexe.

Une distribution de probabilité conjointe décrit simplement la probabilité qu’un individu donné prenne deux valeurs spécifiques pour les variables.

Le mot « conjoint » vient du fait que nous nous intéressons à la probabilité que deux choses se produisent en même temps.

Par exemple, sur un total de 100 individus, 13 étaient des hommes et choisissaient le baseball comme sport préféré.

Ainsi, nous dirions que la probabilité conjointe qu’un individu donné soit un homme et choisisse le baseball comme sport préféré est de 13/100 = 0,13 ou 13 % .

Écrit en notation mathématique :

P(Sexe = Homme, Sport = Baseball) = 13/100 = 0,13 .

Nous pouvons utiliser ce processus pour calculer l’intégralité de la distribution de probabilité conjointe :

• P (Sexe = Homme, Sport = Baseball) = 13/100 = 0,13
• P(Sexe = Homme, Sport = Basket-ball) = 15/100 = 0,15
• P(Sexe = Homme, Sport = Football) = 20/100 = 0,20
• P (Sexe = Femme, Sport = Baseball) = 23/100 = 0,23
• P(Sexe = Féminin, Sport = Basket-ball) = 16/100 = 0,16
• P(Sexe = Féminin, Sport = Football) = 13/100 = 0,13

Notez que la somme des probabilités est égale à 1 , soit 100 % .

Pourquoi utiliser une distribution de probabilité conjointe ?

Les distributions de probabilité conjointes sont utiles car nous collectons souvent des données pour deux variables (comme le sport et le sexe) et nous souhaitons répondre aux questions liées aux deux variables.

Par exemple, nous pourrions vouloir comprendre la probabilité qu’un individu donné dans une population soit un homme et préfère le baseball comme sport favori.

Ou bien nous pourrions être intéressés à comprendre la probabilité qu’un individu donné soit une femme et préfère le football comme sport favori.

Une distribution de probabilité conjointe peut nous aider à répondre à ces questions.

Utilisez les exemples suivants comme entraînement pour mieux comprendre les distributions de probabilité conjointes.

Exemple 1

Le tableau à double entrée suivant présente les résultats d’une enquête qui a demandé à 238 personnes quel genre de film elles préféraient :

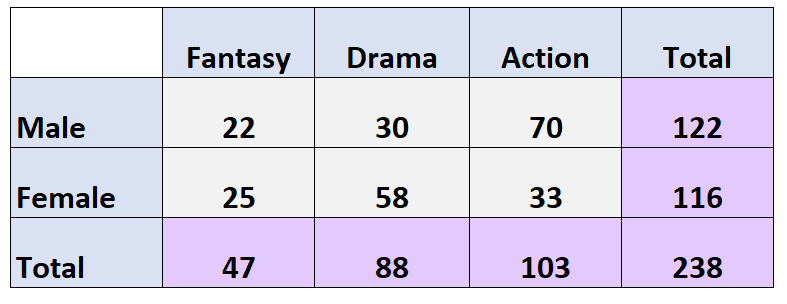
Question : Quelle est la probabilité qu’un individu donné soit une femme et préfère le drame comme genre de film préféré ?

Réponse : P (Genre = Féminin, Genre = Drame) = 58/238 = 0,244 = 24,4 %

Exemple 2

Le tableau bidirectionnel suivant montre les résultats aux examens de 64 étudiants d’une classe en fonction du nombre d’heures qu’ils ont passé à étudier :

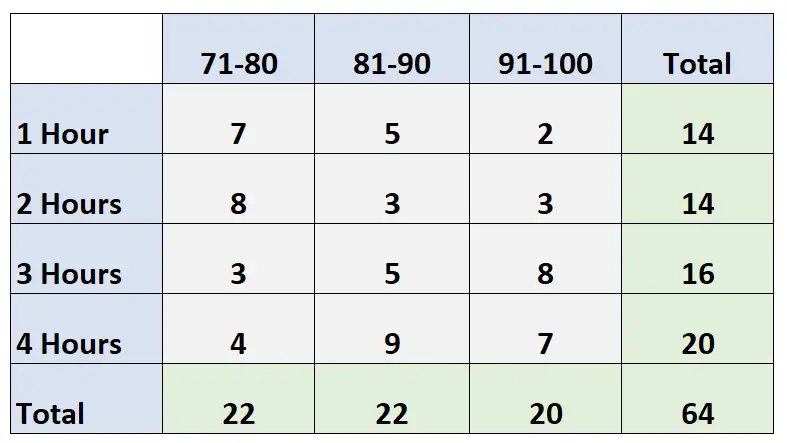
Question : Quelle est la probabilité qu’un individu donné étudie pendant 2 heures et reçoive une note comprise entre 91 et 100 ?

Réponse : P (Étude = 2 heures, Score = 91-100) = 3/64 = 0,047 = 4,7 %

Ressources additionnelles

Qu’est-ce qu’une distribution marginale ?
Comment trouver une fréquence relative conditionnelle dans un tableau à double entrée