Distribution de Weibull

Par Pr Amélia Rodriguez août 3, 2023 Probabilité 0 commentaire

Cet article explique ce qu’est la distribution Weibull et à quoi elle sert. De plus, vous pourrez voir la représentation graphique de la distribution de Weibull et quelles sont les propriétés de ce type de distribution de probabilité.

Qu’est-ce que la distribution de Weibull ?

La distribution de Weibull est une distribution de probabilité continue définie par deux paramètres caractéristiques : le paramètre de forme α et le paramètre d’échelle λ.

En statistiques, la distribution de Weibull est principalement utilisée pour l’analyse de survie. De même, la distribution Weibull a de nombreuses applications dans différents domaines. Nous entrerons ci-dessous en détail sur l’utilisation de la distribution Weibull.

$X\sim\text{Weibull}(\alpha,\lambda)$

Selon les auteurs, la distribution de Weibull peut également être paramétrée avec trois paramètres. Ensuite, un troisième paramètre appelé valeur seuil est ajouté, qui indique l’abscisse à laquelle commence le graphe de distribution.

La distribution de Weibull doit son nom au Suédois Waloddi Weibull, qui l’a décrite en détail en 1951. Cependant, la distribution de Weibull a été découverte par Maurice Fréchet en 1927 et appliquée pour la première fois par Rosin et Rammler en 1933.

Tracé de la distribution de Weibull

Une fois que nous aurons vu la définition de la distribution de Weibull, nous allons voir comment sa représentation graphique varie en fonction des valeurs de ses paramètres.

Ci-dessous, vous pouvez voir plusieurs exemples de la façon dont le graphique de la fonction de densité de la distribution de Weibull varie en fonction de la valeur du paramètre de forme et du paramètre d’échelle.

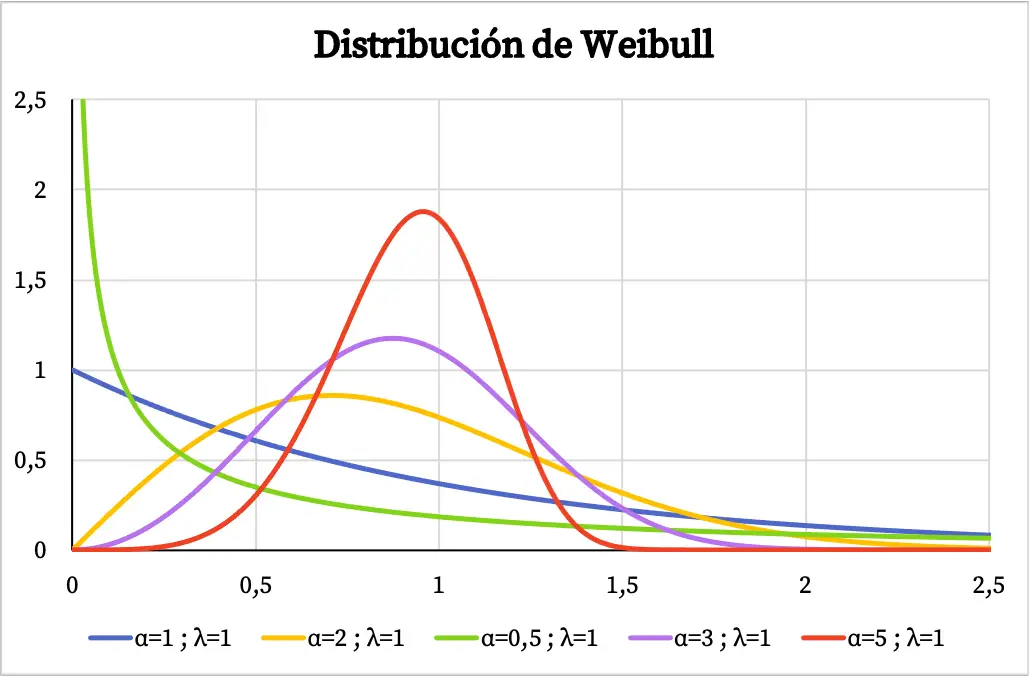
Lorsque la distribution de Weibull est utilisée pour modéliser le taux de défaillance d’un système en fonction du temps, la valeur du paramètre de forme α signifie ce qui suit :

α<1 : le taux de défaillance diminue avec le temps.
α=1 : le taux de défaillance est constant dans le temps.
α>1 : le taux de défaillance augmente avec le temps.

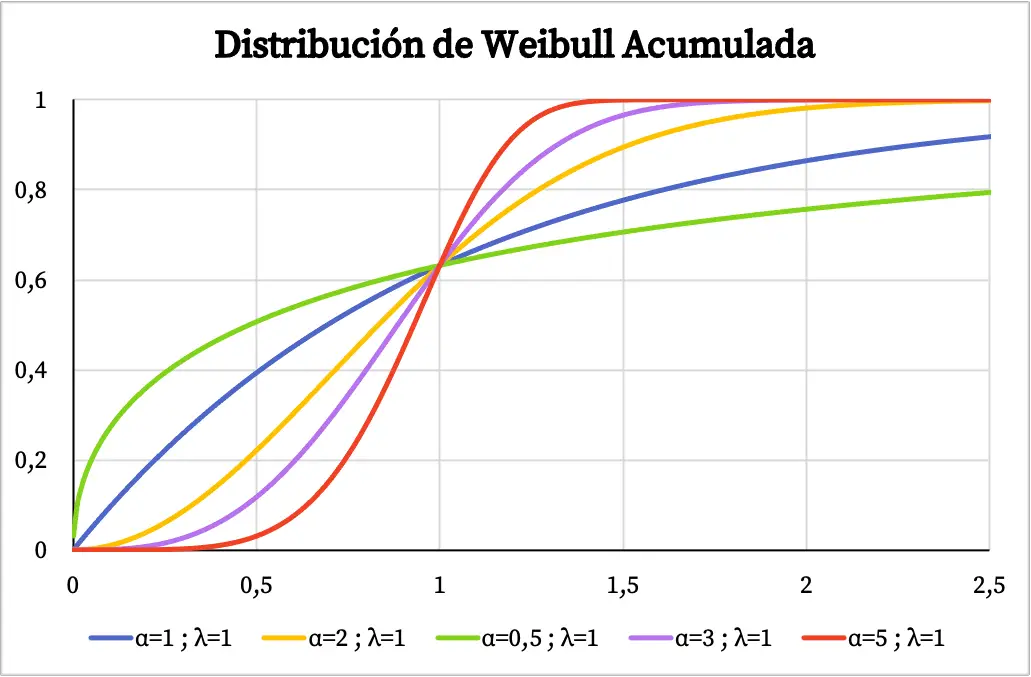
D’autre part, dans le graphique suivant, vous pouvez voir la fonction de probabilité cumulée de la distribution de Weibull représentée en fonction de ses valeurs caractéristiques.

Caractéristiques de la distribution de Weibull

La distribution de Weibull présente les caractéristiques suivantes :

La distribution de Weibull possède deux paramètres caractéristiques qui définissent son graphique : le paramètre de forme α et le paramètre d’échelle λ. Les deux paramètres sont des nombres réels positifs.

$\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}$

La distribution de Weibull n’accepte que les valeurs d’abscisse positives.

$x\in (0,+\infty)$

La moyenne de la distribution de Weibull est calculée avec la formule suivante :

$\displaystyle E[X]=\frac{1}{\lambda}\;\Gamma\left(1+\frac{1}{\alpha}\right)$

D’autre part, la formule pour trouver la variance de la distribution de Weibull est la suivante :

$\displaystyle Var(X)=\frac{1}{\lambda^2}\left[\Gamma\left(1+\frac{2}{\alpha}\right)-\Gamma^2\left(1+\frac{1}{\alpha}\right)\right]$

Le mode d’une variable aléatoire qui suit une distribution de Weibull avec α>1 peut être déterminé par l’expression suivante :

$\displaystyle Mo=\frac{1}{\lambda}\left(\frac{\alpha-1}{\alpha} \right)^{\frac{1}{\alpha}} \quad \text{para } \alpha>1$

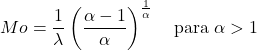
La formule de la fonction de densité de la distribution de Weibull est la suivante :

$\displaystyle P[X=x]=\lambda\alpha(\lambda x)^{\alpha-1}e^{-(\lambda x)^\alpha}$

De même, la formule de la fonction de probabilité cumulative de la distribution de Weibull est la suivante :

$\displaystyle P[X\leq x]=1- e^{-(\lambda x)^\alpha}$

Le coefficient d’asymétrie de la distribution de Weibull est calculé en appliquant la formule suivante :

$\displaystyle A=\frac{\displaystyle\Gamma\left(1+\frac{3}{\alpha}\right)\frac{|}{\lambda^3}-3\mu\sigma^2-\mu^3}{\sigma^3}$

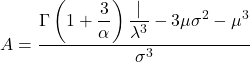
Finalement, la formule qui permet de déterminer le coefficient d’aplatissement de la distribution de Weibull est la suivante :

$\displaystyle C=\frac{\displaystyle\frac{1}{\lambda^4}\Gamma \left(1+\frac{4}{\alpha}\right)-4\gamma_{1}\sigma^3\mu-6\mu^2\sigma^2-\mu^4}{\sigma^4}$

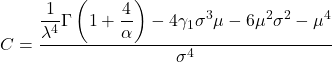
Où

$\Gamma_i=\Gamma\left(1+\frac{i}{\alpha}\right).$

Applications de la distribution de Weibull

La distribution Weibull a de nombreuses applications, parmi lesquelles :

En statistiques appliquées, la distribution de Weibull est utilisée dans l’analyse de survie.
En ingénierie, la distribution de Weibull est utilisée pour modéliser les fonctions liées au temps de fabrication.
Dans les systèmes radar, pour simuler la dispersion du signal reçu.
Dans le secteur des assurances, pour modéliser l’ampleur des sinistres.
En météorologie, par exemple, pour modéliser la fréquence de différentes vitesses de vent.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus