Qu’est-ce qu’une distribution d’échantillonnage ?

Imaginez qu’il existe une population de 10 000 dauphins et que le poids moyen d’un dauphin dans cette population est de 300 livres.

Si nous prenons un échantillon aléatoire simple de 50 dauphins de cette population, nous pourrions constater que le poids moyen des dauphins de cet échantillon est de 305 livres.

Ensuite, si nous prenons un autre échantillon aléatoire simple de 50 dauphins, nous pourrions constater que le poids moyen des dauphins de cet échantillon est de 295 livres.

Chaque fois que nous prenons un échantillon aléatoire simple de 50 dauphins, il est probable que le poids moyen des dauphins dans l’échantillon soit proche de la moyenne de la population de 300 livres, mais pas exactement de 300 livres.

Imaginons que nous prenions 200 échantillons aléatoires simples de 50 dauphins de cette population et que nous créions un histogramme du poids moyen de chaque échantillon :

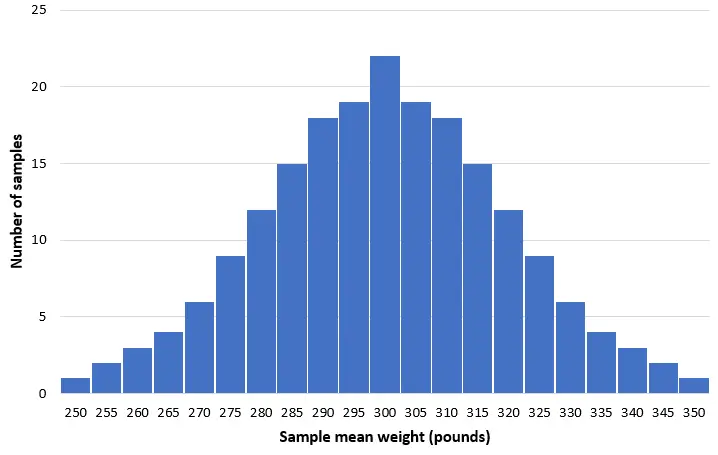
Dans la plupart des échantillons, le poids moyen sera proche de 300 livres. Dans de rares cas, nous pouvons prélever un échantillon rempli de petits dauphins dont le poids moyen n’est que de 250 livres. Ou encore, il se peut que nous prélevions un échantillon rempli de grands dauphins dont le poids moyen est de 350 livres. En général, la distribution des moyennes de l’échantillon sera approximativement normale, le centre de la distribution étant situé au véritable centre de la population.

Cette distribution des moyennes d’échantillon est connue sous le nom de distribution d’échantillonnage de la moyenne et possède les propriétés suivantes :

_µx = µ

où μ _x est la moyenne de l’échantillon et μ est la moyenne de la population.

σ _x = σ/ √n

où σ _x est l’écart type de l’échantillon, σ est l’écart type de la population et n est la taille de l’échantillon.

Par exemple, dans cette population de dauphins, nous savons que le poids moyen est μ = 300. La moyenne de la distribution d’échantillonnage est donc μ _x = 300 .

Supposons que nous sachions également que l’écart type de la population est de 18 livres. L’écart type de l’échantillon est donc σ _x = 18/ √50 = 2,546 .

Distribution d’échantillonnage de la proportion

Considérons la même population de 10 000 dauphins. Supposons que 10 % des dauphins soient noirs et que le reste soit gris. Supposons que nous prenions un échantillon aléatoire simple de 50 dauphins et constations que 14 % des dauphins de cet échantillon sont noirs. Ensuite, nous prenons un autre échantillon aléatoire simple de 50 dauphins et constatons que 8 % des dauphins de cet échantillon sont noirs.

Imaginez que nous prenions 200 échantillons aléatoires simples de 50 dauphins de cette population et que nous créions un histogramme de la proportion de dauphins noirs dans chaque échantillon :

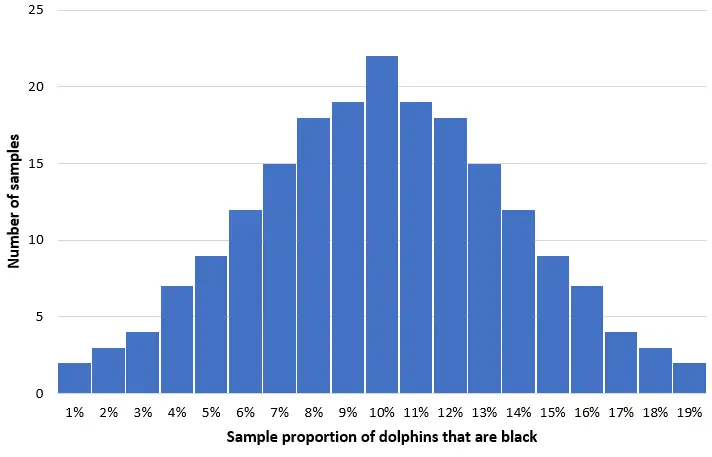
Dans la plupart des échantillons, la proportion de dauphins noirs sera proche de la population réelle de 10 %. La distribution de la proportion de l’échantillon de dauphins noirs sera à peu près normale, le centre de la distribution étant situé au véritable centre de la population.

Cette distribution des proportions d’échantillon est connue sous le nom de distribution d’échantillonnage de la proportion et possède les propriétés suivantes :

_µp = P

où p est la proportion de l’échantillon et P est la proportion de la population.

σ _p = √ (P)(1-P) / n

où P est la proportion de population et n est la taille de l’échantillon.

Par exemple, dans cette population de dauphins, nous savons que la véritable proportion de dauphins noirs est de 10 % = 0,1. Ainsi, la moyenne de la distribution d’échantillonnage de la proportion est μ _p = 0,1 .

Supposons que nous sachions également que l’écart type de la population est de 18 livres. Ainsi, l’écart type de l’échantillon est σ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 .

Établir la normalité

Pour utiliser les formules ci-dessus, la distribution d’échantillonnage doit être normale.

Selon le théorème central limite , la distribution d’échantillonnage d’une moyenne d’échantillon est approximativement normale si la taille de l’échantillon est suffisamment grande, même si la distribution de la population n’est pas normale . Dans la plupart des cas, nous considérons qu’un échantillon de 30 personnes ou plus est suffisamment grand.

La distribution d’échantillonnage d’une proportion d’échantillon est à peu près normale si le nombre attendu de réussites et d’échecs est tous deux d’au moins 10.

Exemples

Nous pouvons utiliser des distributions d’échantillonnage pour calculer des probabilités.

Exemple 1 : Une certaine machine crée des cookies. La répartition du poids de ces cookies est asymétrique vers la droite avec une moyenne de 10 onces et un écart type de 2 onces. Si nous prenons un échantillon aléatoire simple de 100 cookies produits par cette machine, quelle est la probabilité que le poids moyen des cookies de cet échantillon soit inférieur à 9,8 onces ?

Étape 1 : Établir la normalité.

Nous devons nous assurer que la distribution d’échantillonnage de la moyenne de l’échantillon est normale. Puisque la taille de notre échantillon est supérieure ou égale à 30, selon le théorème central limite, nous pouvons supposer que la distribution d’échantillonnage de la moyenne de l’échantillon est normale.

Étape 2 : Trouvez la moyenne et l’écart type de la distribution d’échantillonnage.

_µx = µ

σ _x = σ/ √n

μ _x = 10 onces

σ _x = 2/ √100 = 2/10 = 0,2 once

Étape 3 : Utilisez le calculateur de zone de score Z pour déterminer la probabilité que le poids moyen des cookies de cet échantillon soit inférieur à 9,8 onces.

Entrez les nombres suivants dans le calculateur de zone de score Z. Vous pouvez laisser « Score brut 2 » vide puisque nous ne trouvons qu’un seul chiffre dans cet exemple.

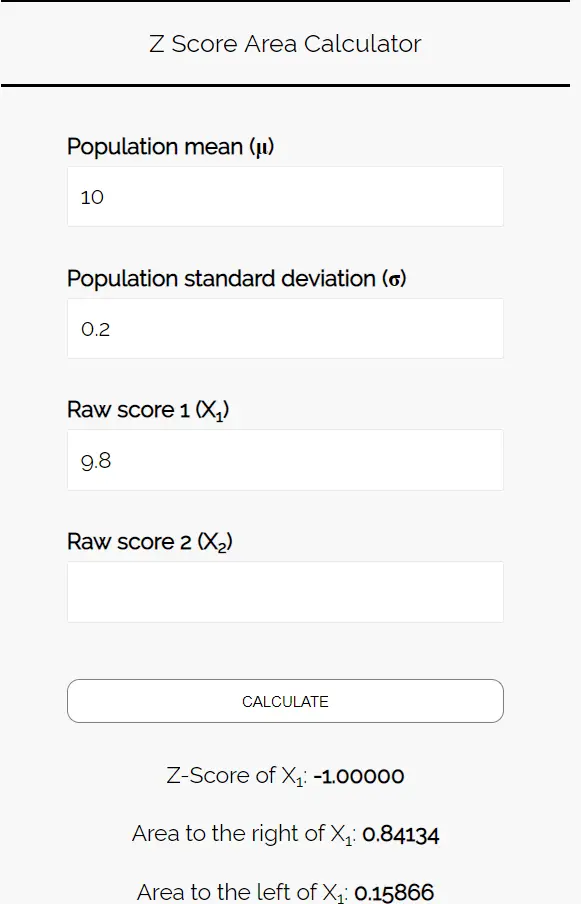
Puisque nous voulons connaître la probabilité que le poids moyen des biscuits dans cet échantillon soit inférieur à 9,8 onces, nous nous intéressons à la zone à gauche de 9,8. Le calculateur nous indique que cette probabilité est de 0,15866 .

Exemple 2 : Selon une étude menée à l’échelle de l’école, 87 % des élèves d’une école particulière préfèrent la pizza à la glace. Supposons que nous prenions un échantillon aléatoire simple de 200 étudiants. Quelle est la probabilité que la proportion d’élèves préférant la pizza soit inférieure à 85 % ?

Étape 1 : Établir la normalité.

Rappelons que la distribution d’échantillonnage d’une proportion d’échantillon est approximativement normale si le nombre attendu de « réussites » et d’« échecs » est tous deux d’au moins 10.

Dans ce cas, le nombre attendu d’étudiants qui préféreront la pizza est de 87 % * 200 étudiants = 174 étudiants. Le nombre attendu d’étudiants qui ne préféreront pas la pizza est de 13% * 200 étudiants = 26 étudiants. Puisque ces deux nombres sont au moins 10, nous pouvons supposer que la distribution d’échantillonnage de la proportion d’élèves qui préféreront la pizza est à peu près normale.

Étape 2 : Trouvez la moyenne et l’écart type de la distribution d’échantillonnage.

_µp = P

σ _p = √ (P)(1-P) / n

_µp = 0,87

σ _p = √ (0,87)(1-0,87) / 200 = 0,024

Étape 3 : Utilisez le calculateur de zone de score Z pour déterminer la probabilité que la proportion d’élèves préférant la pizza soit inférieure à 85 %.

Entrez les nombres suivants dans le calculateur de zone de score Z. Vous pouvez laisser « Score brut 2 » vide puisque nous ne trouvons qu’un seul chiffre dans cet exemple.

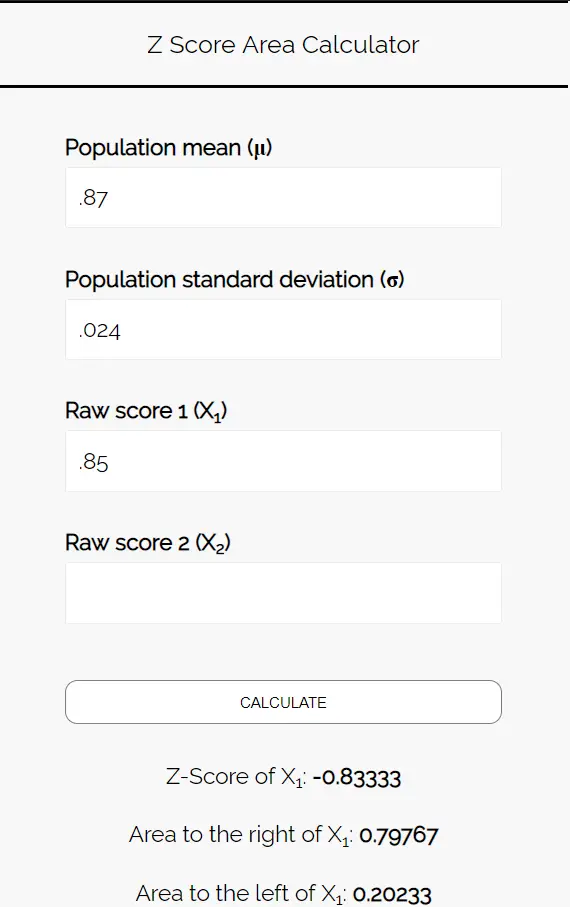
Puisque nous voulons connaître la probabilité que la proportion d’étudiants préférant la pizza soit inférieure à 85 %, nous nous intéressons à l’aire à gauche de 0,85. Le calculateur nous indique que cette probabilité est de 0,20233 .