Comment calculer les distributions d’échantillonnage dans R

Une distribution d’échantillonnage est une distribution de probabilité d’une certaine statistique basée sur de nombreux échantillons aléatoires provenant d’une seule population.

Ce didacticiel explique comment effectuer les opérations suivantes avec des distributions d’échantillonnage dans R :

• Générez une distribution d’échantillonnage.
• Visualisez la distribution d’échantillonnage.
• Calculez la moyenne et l’écart type de la distribution d’échantillonnage.
• Calculer les probabilités concernant la distribution d’échantillonnage.

Générer une distribution d’échantillonnage dans R

Le code suivant montre comment générer une distribution d’échantillonnage dans R :

#make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep(NA, n)

#fill empty vector with means
for(i in 1:n){
  sample_means[i] = mean(rnorm(20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656

Dans cet exemple, nous avons utilisé la fonction rnorm() pour calculer la moyenne de 10 000 échantillons dans lesquels chaque taille d’échantillon était de 20 et a été généré à partir d’une distribution normale avec une moyenne de 5,3 et un écart type de 9.

Nous pouvons voir que le premier échantillon avait une moyenne de 5,283992, le deuxième échantillon avait une moyenne de 6,304845, et ainsi de suite.

Visualisez la distribution d’échantillonnage

Le code suivant montre comment créer un histogramme simple pour visualiser la distribution d’échantillonnage :

#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = "Sample Means", col = "steelblue")

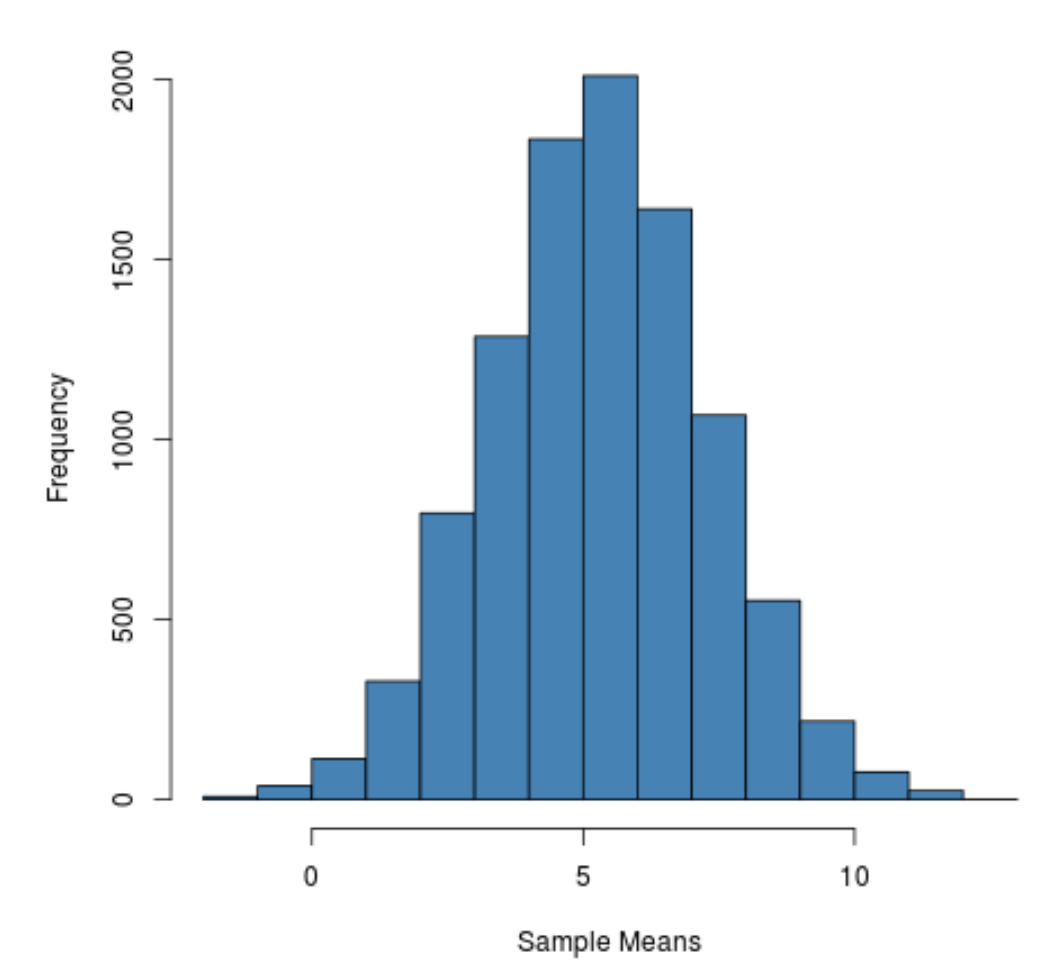
On peut voir que la distribution d’échantillonnage est en forme de cloche avec un pic proche de la valeur 5.

Toutefois, à partir des queues de la distribution, nous pouvons voir que certains échantillons avaient des moyennes supérieures à 10 et d’autres des moyennes inférieures à 0.

Trouver la moyenne et l’écart type

Le code suivant montre comment calculer la moyenne et l’écart type de la distribution d’échantillonnage :

#mean of sampling distribution
mean(sample_means)

[1] 5.287195

#standard deviation of sampling distribution
sd(sample_means)

[1] 2.00224

Théoriquement, la moyenne de la distribution d’échantillonnage devrait être de 5,3. Nous pouvons voir que la moyenne d’échantillonnage réelle dans cet exemple est de 5,287195 , ce qui est proche de 5,3.

Et théoriquement, l’écart type de la distribution d’échantillonnage devrait être égal à s/√n, ce qui serait 9 / √20 = 2,012. Nous pouvons voir que l’écart type réel de la distribution d’échantillonnage est de 2,00224 , ce qui est proche de 2,012.

Calculer les probabilités

Le code suivant montre comment calculer la probabilité d’obtenir une certaine valeur pour une moyenne d’échantillon, en fonction d’une moyenne de population, de l’écart type de la population et de la taille de l’échantillon.

#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

Dans cet exemple particulier, nous trouvons la probabilité que la moyenne de l’échantillon soit inférieure ou égale à 6, étant donné que la moyenne de la population est de 5,3, l’écart type de la population est de 9 et la taille de l’échantillon de 20 est de 0,6417 .

Ceci est très proche de la probabilité calculée par le Sampling Distribution Calculator :

Le code complet

Le code R complet utilisé dans cet exemple est présenté ci-dessous :

#make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep(NA, n)

#fill empty vector with means
for(i in 1:n){
  sample_means[i] = mean(rnorm(20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = "Sample Means", col = "steelblue")

#mean of sampling distribution
mean(sample_means)

#standard deviation of sampling distribution
sd(sample_means)

#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

Ressources additionnelles

Une introduction aux distributions d’échantillonnage
Calculateur de distribution d’échantillonnage
Une introduction au théorème central limite