Distribution du chi carré
Cet article explique ce qu’est la distribution du chi carré et à quoi elle sert. De plus, vous trouverez le graphique de la distribution du chi carré et ses propriétés.
Quelle est la distribution du chi carré ?
La distribution du Chi carré est une distribution de probabilité dont le symbole est χ². Plus précisément, la distribution du Chi carré est la somme du carré de k variables aléatoires indépendantes avec une distribution normale.
Ainsi, la distribution du Chi carré a k degrés de liberté. Par conséquent, une distribution du Chi carré a autant de degrés de liberté que la somme des carrés des variables normalement distribuées qu’elle représente.
![Rendered by QuickLaTeX.com \displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-9ea0bf7a87071883ceae5e419bae9e71_l3.png)
La distribution du Chi carré est également connue sous le nom de distribution de Pearson .
Il convient de noter que la distribution du Chi carré est un cas particulier de la distribution gamma.
La distribution du chi carré est largement utilisée dans l’inférence statistique, par exemple dans les tests d’hypothèses et les intervalles de confiance. Nous verrons ci-dessous quelles sont les applications de ce type de distribution de probabilité.
Graphique de la distribution du chi carré
Une fois que nous aurons vu la définition de la distribution du Chi carré, nous allons voir plusieurs exemples de ce type de distribution représentés graphiquement. Ainsi, ci-dessous, vous pouvez voir comment le graphique de probabilité de la distribution du chi carré varie en fonction des degrés de liberté.
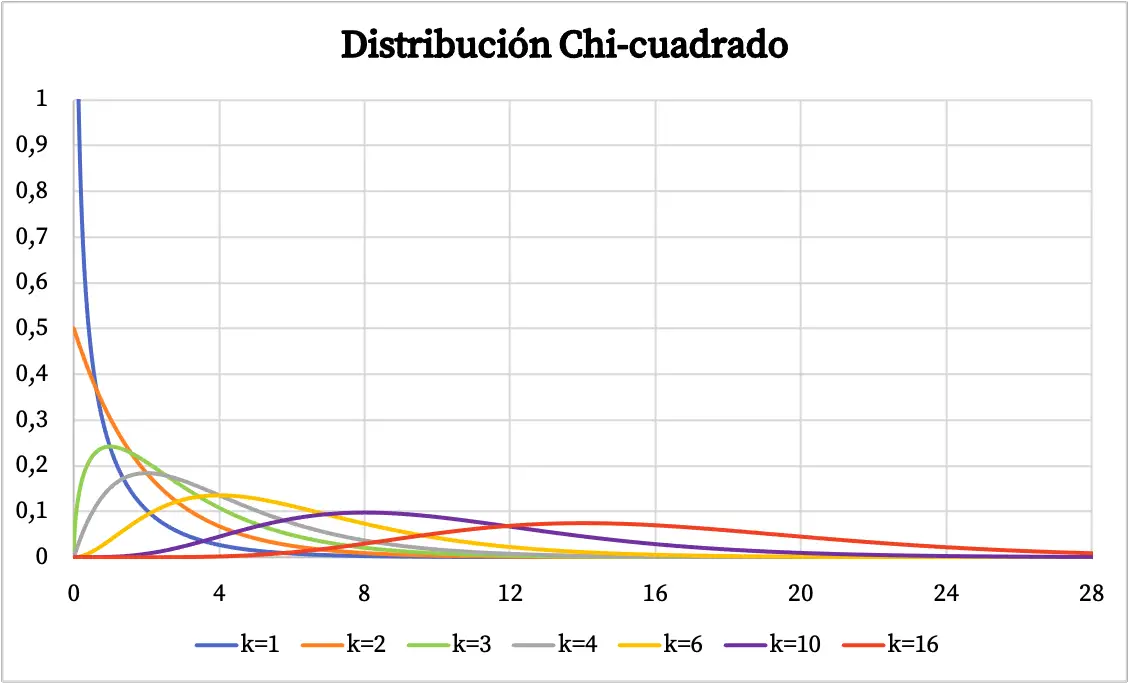
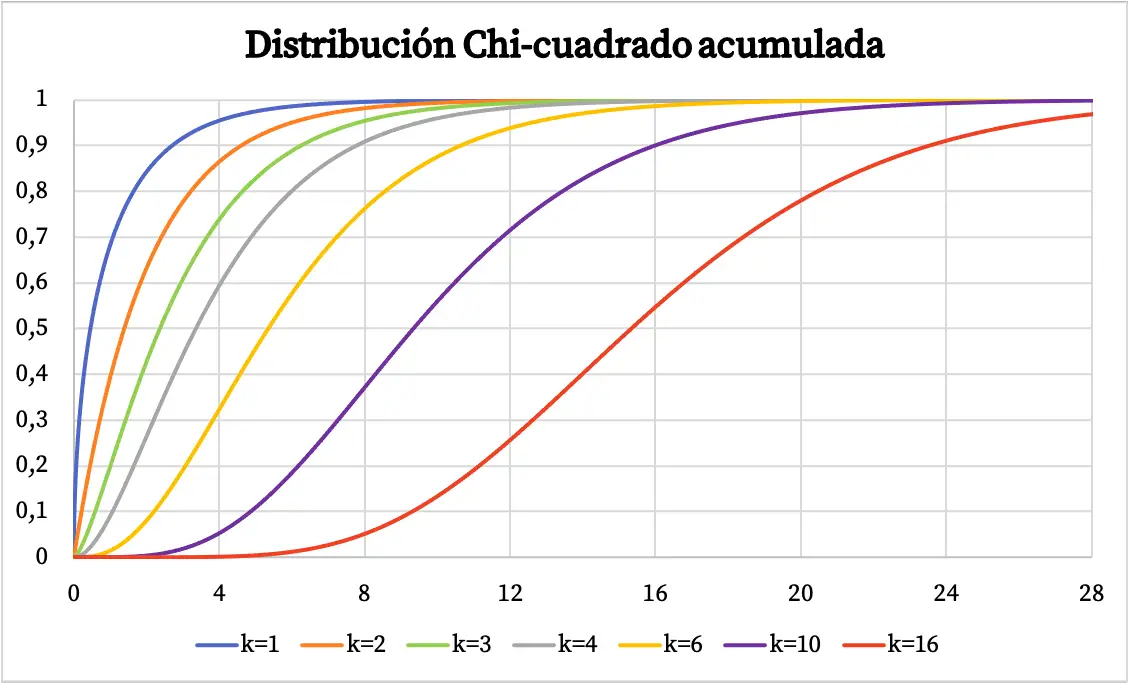
La fonction de densité de la distribution du Chi carré a été représentée dans le graphique ci-dessus. D’autre part, le graphique de la fonction de distribution de probabilité cumulée du chi carré est le suivant :
Caractéristiques de la distribution du chi carré
Dans cette section, nous verrons les propriétés les plus importantes de la distribution du Chi carré liées à la théorie des probabilités et aux statistiques.
- La moyenne d’une distribution du chi carré est égale à ses degrés de liberté.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8a7926aa60ec788064c47a5a34e641ab_l3.png)
- La variance d’une distribution du Chi carré équivaut à deux fois les degrés de liberté de la distribution.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-cffd659f19d8ed8260fcaf53dc6dd83f_l3.png)
- Le mode d’une distribution du chi carré est inférieur de deux unités à ses degrés de liberté, tant que la distribution a plus d’un degré de liberté.
![]()
- La fonction de densité de la distribution du Chi carré est nulle si x=0. Cependant, pour les valeurs de x supérieures à 0, la fonction de densité d’une distribution du Chi carré est définie par la formule suivante :
![]()
- La fonction de distribution cumulative de la distribution du Chi carré est régie par la formule suivante :
![]()
- Le coefficient d’asymétrie de la distribution du Chi carré est la racine carrée du quotient de huit divisé par le nombre de degrés de liberté de la distribution.
![]()
- L’aplatissement de la distribution du Chi carré est calculé à l’aide de l’expression suivante :
![]()
- En raison du théorème central limite, la distribution du chi carré peut être approximée par une distribution normale si k est suffisamment grand.
![]()
Applications de la distribution du chi carré
La distribution du chi carré a de nombreuses applications différentes en statistiques. En fait, il existe même le test du chi carré qui est utilisé pour vérifier l’indépendance entre les variables et la qualité de l’ajustement à une distribution théorique. Par exemple, le test du Chi carré peut être utilisé pour déterminer si les données d’un échantillon sont conformes à une distribution de Poisson.
Dans l’analyse de régression linéaire, la distribution du chi carré est également utilisée pour estimer la moyenne d’une population normalement distribuée et pour estimer la pente de la droite d’étude de régression linéaire.
Enfin, la distribution du Chi carré participe également à l’analyse de variance, de par sa relation avec la distribution Snedecor F.
