Comment utiliser la distribution exponentielle dans Excel

La distribution exponentielle est une distribution de probabilité utilisée pour modéliser le temps que nous devons attendre jusqu’à ce qu’un certain événement se produise.

Cette distribution peut être utilisée pour répondre à des questions telles que :

• Combien de temps un commerçant doit-il attendre qu’un client entre dans son magasin ?
• Combien de temps une batterie continuera-t-elle à fonctionner avant de mourir ?
• Combien de temps un ordinateur continuera-t-il à fonctionner avant de tomber en panne ?

Dans chaque scénario, nous souhaitons calculer combien de temps nous devrons attendre jusqu’à ce qu’un certain événement se produise. Ainsi, chaque scénario pourrait être modélisé à l’aide d’une distribution exponentielle.

Si une variable aléatoire X suit une distribution exponentielle, alors la fonction de densité cumulée de X peut s’écrire :

F (x; λ) = 1 – e ^-λx

où:

• λ : le paramètre de taux (calculé comme λ = 1/μ)
• e : Une constante à peu près égale à 2,718

Pour calculer les probabilités liées à la fonction de densité cumulée de la distribution exponentielle dans Excel, on peut utiliser la formule suivante :

=EXPON.DIST(x, lambda, cumulative)

où:

• x : la valeur de la variable aléatoire distribuée exponentiellement
• lambda : le paramètre rate
• cumulative : s’il faut utiliser ou non la fonction de densité cumulée (VRAI ou FAUX)

Les exemples suivants montrent comment utiliser cette formule dans la pratique.

Exemple 1 : délai jusqu’à l’arrivée du prochain client

Un nouveau client entre dans un magasin toutes les deux minutes en moyenne. Après l’arrivée d’un client, déterminez la probabilité qu’un nouveau client arrive en moins d’une minute.

Solution : Le temps moyen entre les clients est de deux minutes. Ainsi, le taux peut être calculé comme suit :

• λ = 1/µ
• λ = 1/2
• λ = 0,5

Ainsi, on peut utiliser la formule suivante dans Excel pour calculer la probabilité qu’un nouveau client arrive en moins d’une minute :

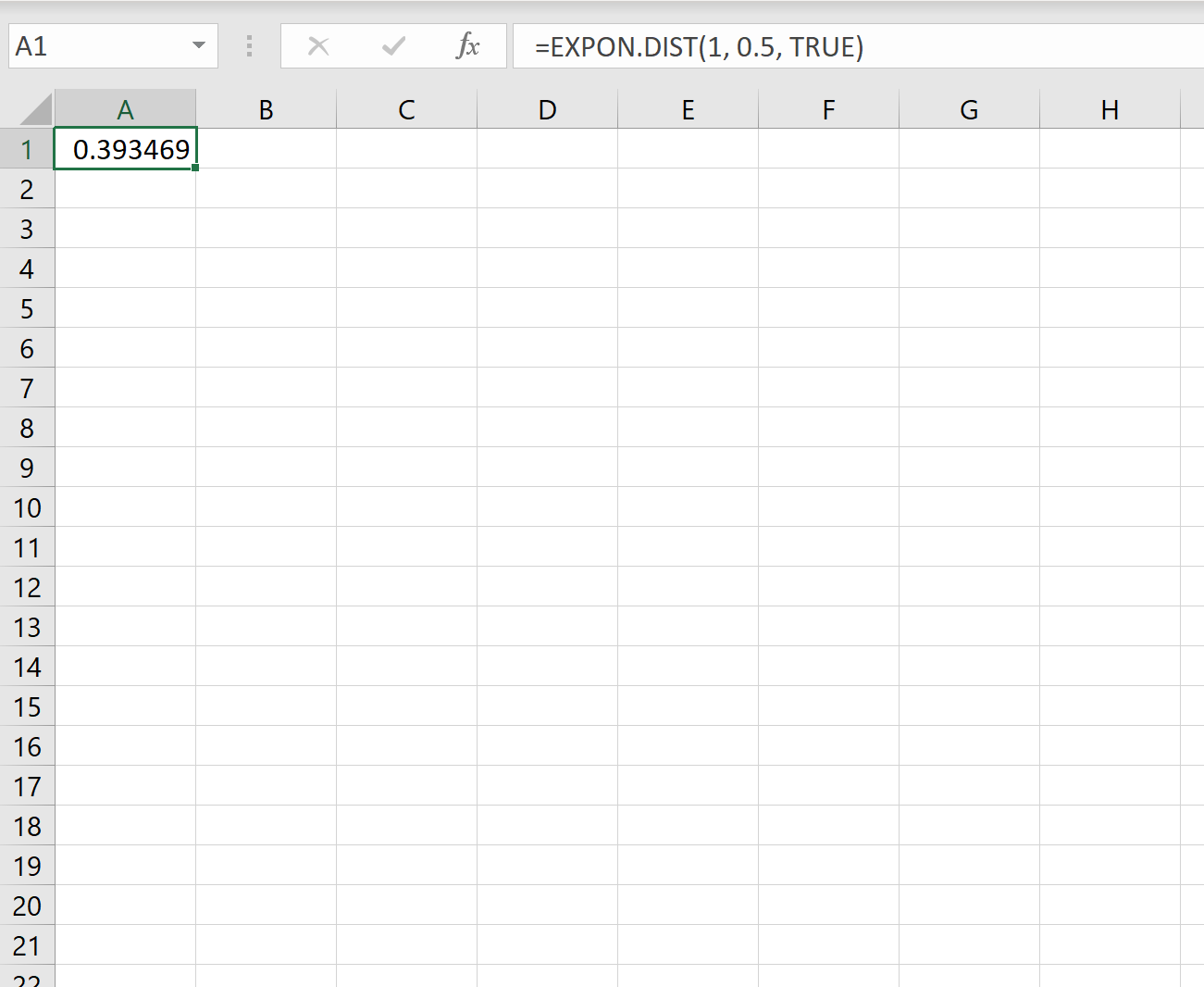
La probabilité que nous devions attendre moins d’une minute pour l’arrivée du prochain client est de 0,393469 .

Exemple 2 : Délai jusqu’au prochain tremblement de terre

Supposons qu’un tremblement de terre se produise en moyenne tous les 400 jours dans une certaine région. Après un tremblement de terre, déterminez la probabilité qu’il faudra plus de 500 jours avant que le prochain tremblement de terre ne se produise.

Solution : Le délai moyen entre les tremblements de terre est de 400 jours. Ainsi, le taux peut être calculé comme suit :

• λ = 1/µ
• λ = 1/400
• λ = 0,0025

Ainsi, nous pouvons utiliser la formule suivante dans Excel pour calculer la probabilité que le prochain séisme mette moins de 500 jours à se produire :

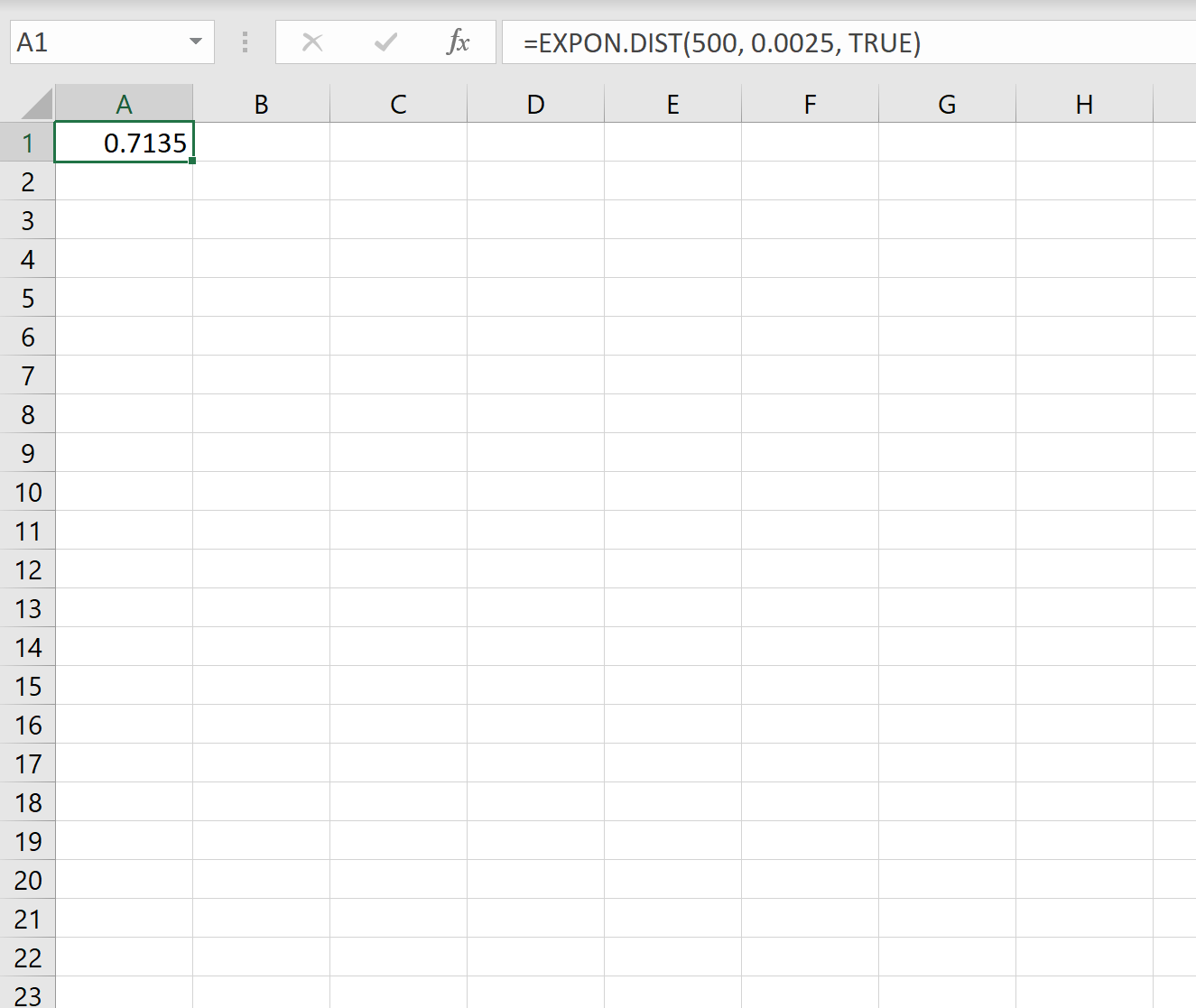
La probabilité qu’il faudra moins de 500 jours avant le prochain séisme est de 0,7135.

Ainsi, la probabilité que nous devions attendre plus de 500 jours pour le prochain tremblement de terre est de 1 – 0,7135 = 0,2865 .

Exemple 3 : durée jusqu’au prochain appel téléphonique

Supposons qu’un centre d’appels reçoive un nouvel appel toutes les 10 minutes en moyenne. Après qu’un client appelle, déterminez la probabilité qu’un nouveau client appelle dans les 10 à 15 minutes.

Solution : Le temps moyen entre les appels est de 10 minutes. Ainsi, le taux peut être calculé comme suit :

• λ = 1/µ
• λ = 1/10
• λ = 0,1

Ainsi, on peut utiliser la formule suivante dans Excel pour calculer la probabilité que le prochain client appelle dans les 10 à 15 minutes :

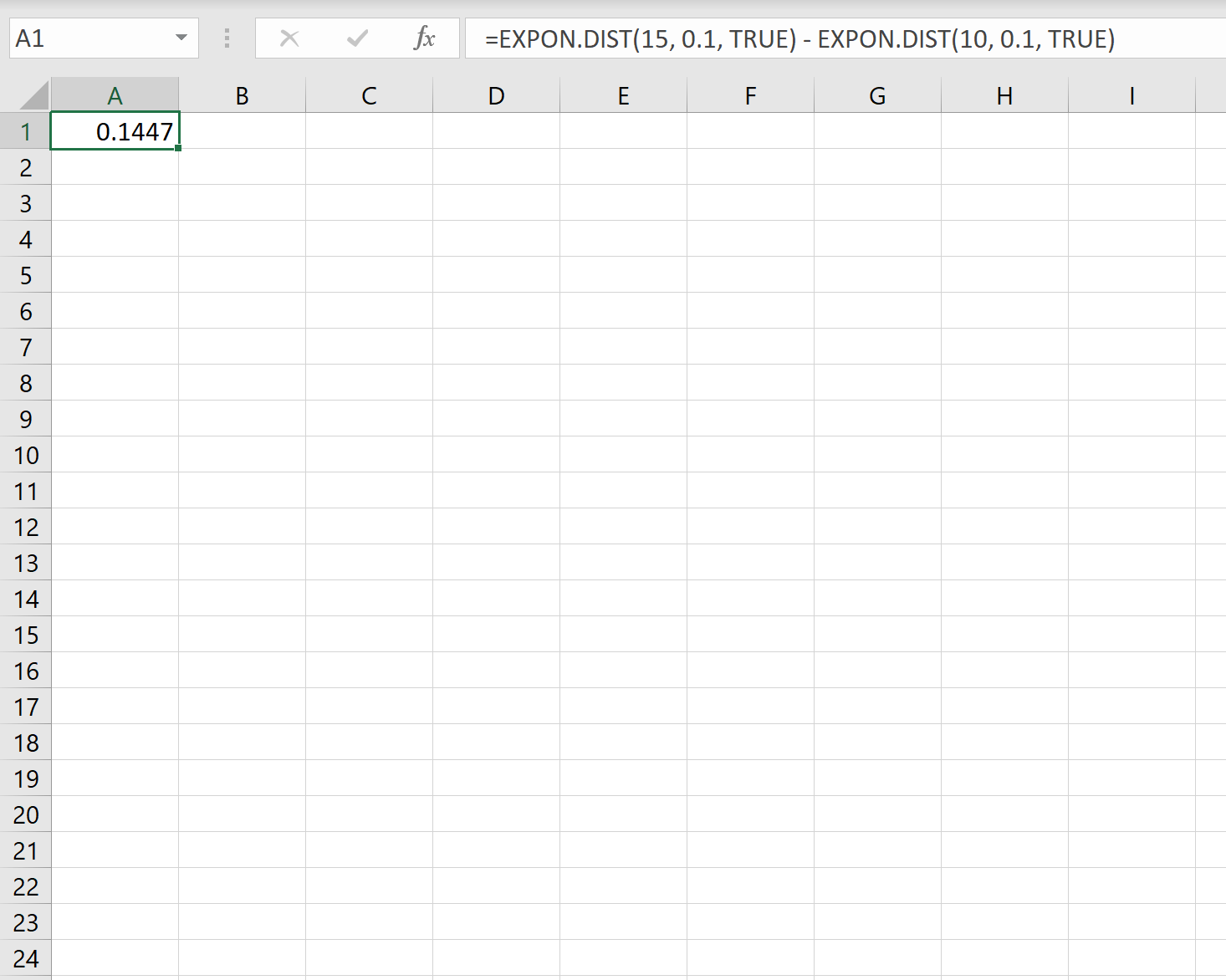
La probabilité qu’un nouveau client appelle dans les 10 à 15 minutes. est 0,1447 .

Ressources additionnelles

Une introduction à la distribution exponentielle
La propriété sans mémoire de la distribution exponentielle
Comment tracer une distribution exponentielle dans R