Distribution gamma

Par août 3, 2023 Probabilité 0 commentaire

Cet article explique ce qu’est la distribution gamma et à quoi elle sert. Ainsi, vous retrouverez la définition de la distribution gamma, ses propriétés et à quoi ressemble sa représentation graphique.

Quelle est la distribution gamma ?

La distribution gamma est une distribution de probabilité continue définie par deux paramètres caractéristiques, α et λ. Autrement dit, la distribution gamma dépend de la valeur de ses deux paramètres : α est le paramètre de forme et λ est le paramètre d’échelle.

Le symbole de la distribution gamma est la lettre grecque majuscule Γ. Ainsi, si une variable aléatoire suit une distribution gamma, elle s’écrit comme suit :

X\sim \Gamma(\alpha,\lambda)

La distribution gamma peut également être paramétrée à l’aide du paramètre de forme k = α et du paramètre d’échelle inverse θ = 1/λ. Dans tous les cas, les deux paramètres qui définissent la distribution gamma sont des nombres réels positifs.

En général, la distribution gamma est utilisée pour modéliser des ensembles de données asymétriques vers la droite, de sorte qu’il y ait une plus grande concentration de données sur le côté gauche du graphique. Par exemple, la distribution gamma est utilisée pour modéliser la fiabilité des composants électriques.

Diagramme de distribution gamma

Le graphique de la distribution gamma dépend des valeurs de ses paramètres caractéristiques. Ci-dessous, vous pouvez voir comment la fonction de densité de la distribution gamma varie en fonction du paramètre de forme et du paramètre d’échelle.

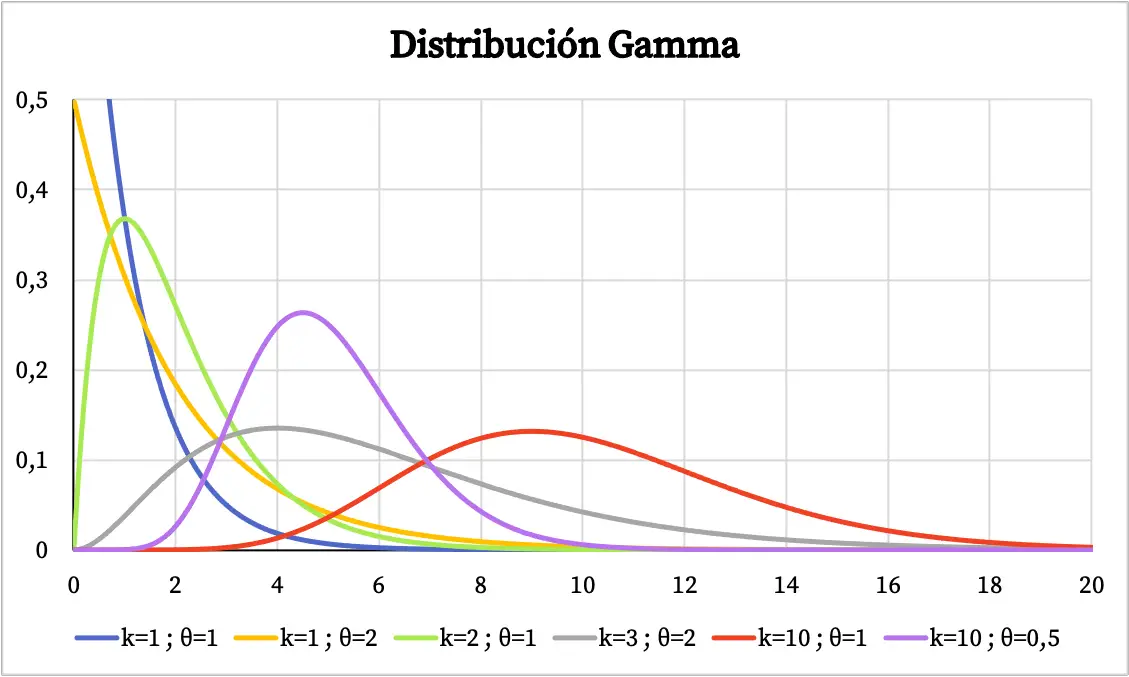
graphique de distribution gamma

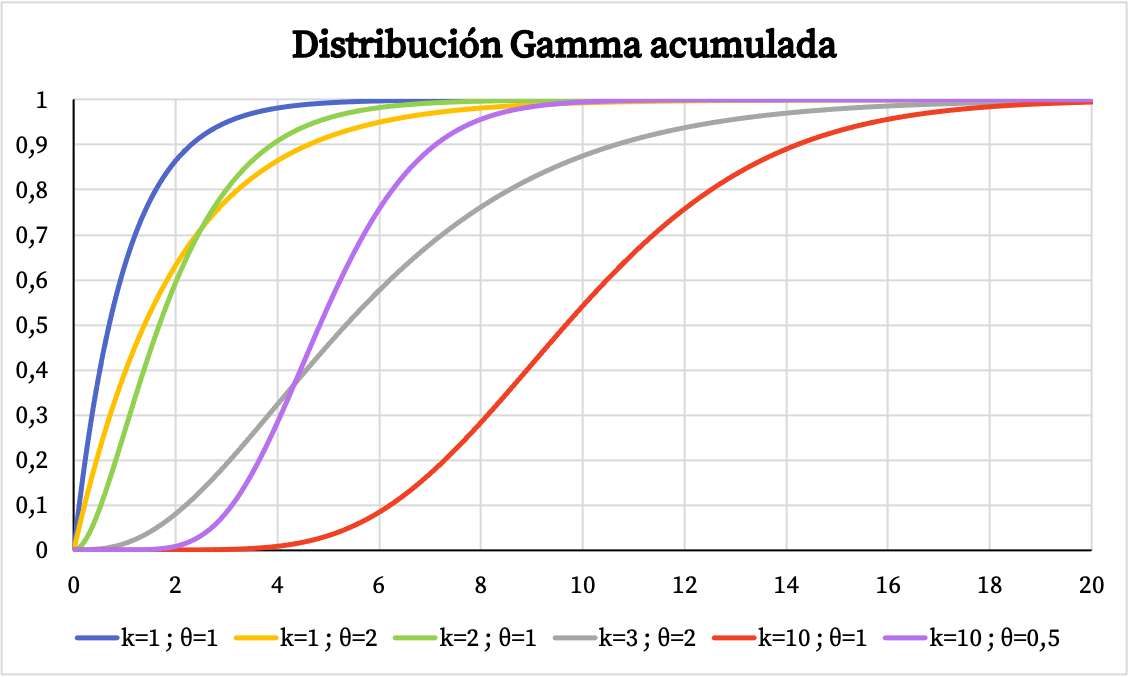
D’autre part, vous pouvez voir ci-dessous le graphique de la fonction de probabilité cumulée de la distribution gamma :

graphique de la fonction de probabilité cumulée de la distribution Gamm

Caractéristiques de la distribution gamma

Nous allons ensuite voir quelles sont les caractéristiques de la distribution gamma.

  • Le graphique de la distribution gamma est entièrement défini par ses deux paramètres caractéristiques : α est le paramètre de forme et λ est le paramètre d’échelle.

\alpha , \lambda >0

  • Le domaine de la distribution gamma est composé uniquement de nombres positifs.

x\in (0,+\infty)

  • La moyenne de la distribution gamma est égale au rapport entre le paramètre de forme et le paramètre d’échelle, c’est-à-dire α/λ.

E[X]=\cfrac{\alpha}{\lambda}

  • La variance de la distribution gamma est équivalente au paramètre de forme divisé par le carré du paramètre d’échelle.

Var(X)=\cfrac{\alpha}{\lambda^2}

  • Pour les valeurs de α inférieures à 1, le mode est 0. Mais si α est égal ou supérieur à 1, le mode de la distribution gamma peut être calculé avec la formule suivante :

\begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}

  • La formule de la fonction de densité de la distribution gamma est la suivante :

\displaystyle f(x)=\frac{\lambda(\lambda x)^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}

Où Γ est la fonction gamma, qui est définie comme :

\displaystyle \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}dt

  • La formule de la distribution cumulative d’une variable aléatoire définie par une distribution gamma est la suivante :

\displaystyle F(x)=\int_0^x\frac{\lambda(\lambda y)^{\alpha-1}e^{-\lambda y}}{\Gamma(\alpha)}\;dy

  • Si le paramètre de forme α est égal à 1, alors la distribution gamma est équivalente à une distribution exponentielle avec le même paramètre d’échelle λ.

X\sim \Gamma(1,\lambda) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \text{Exp}(\lambda)

  • Lorsque le paramètre d’échelle λ est une moyenne, alors la distribution gamma est un cas particulier de la distribution du chi carré .

\displaystyle X\sim \Gamma\left(\frac{n}{2},\frac{1}{2}\right) \text{con } n\in \mathbb{N}\ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \chi_n^2

à propos de l'auteur

Amelia Rodriguez
Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus

Ajouter un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *