Distribution hypergéométrique

Par Pr Amélia Rodriguez août 6, 2023 Probabilité 0 commentaire

Dans cet article, nous expliquons ce qu’est la distribution hypergéométrique et comment une probabilité est calculée avec ce type de distribution. Vous trouverez en ligne la formule de la distribution hypergéométrique, quelles sont ses caractéristiques, ainsi qu’un calculateur pour calculer la probabilité de la distribution hypergéométrique.

Quelle est la distribution hypergéométrique ?

La distribution hypergéométrique est une distribution de probabilité qui décrit le nombre de cas de réussite dans une extraction aléatoire sans remplacement de n éléments d’une population.

Autrement dit, la distribution hypergéométrique est utilisée pour calculer la probabilité d’obtenir x succès lors de l’extraction de n éléments d’une population sans en remplacer aucun.

La distribution hypergéométrique a trois paramètres :

N : est le nombre d’éléments dans la population (N = 0, 1, 2,…).
K : est le nombre maximum de cas de réussite (K = 0, 1, 2,…,N). Puisque dans une distribution hypergéométrique un élément ne peut être considéré que comme un « succès » ou un « échec », NK est le nombre maximum de cas d’échec.
n : est le nombre d’extractions sans remise qui sont effectuées.

$X \sim HG(N,K,n)$

Par exemple, une variable aléatoire discrète X qui a une distribution hypergéométrique avec les paramètres N=8, K=5 et n=3 est définie comme suit :

$X \sim HG(8,5,3)$

Formule de distribution hypergéométrique

La formule de la distribution hypergéométrique est le produit du nombre combinatoire de K sur x par le nombre combinatoire de NK sur nx divisé par le nombre combinatoire de N sur n .

Où N est la taille de la population, K est le nombre total de cas favorables, n est le nombre d’extractions sans remplacement et x est le nombre de cas favorables pour lesquels il faut calculer la probabilité d’occurrence.

Vous pouvez utiliser la calculatrice ci-dessous pour calculer la probabilité d’un événement d’une variable qui suit la distribution hypergéométrique.

Exemple de distribution hypergéométrique

Une fois que nous avons vu la définition et la formule de la distribution hypergéométrique, nous allons maintenant résoudre un exemple étape par étape afin que vous sachiez comment calculer la probabilité d’une distribution hypergéométrique.

Dans un sac, nous mettons 20 boules bleues et 30 boules rouges, c’est-à-dire qu’il y a 50 boules au total à l’intérieur du sac. Si l’on tire 12 boules sans en remplacer aucune, trouvez la probabilité de tirer 4 boules bleues.

La première chose que nous devons faire pour résoudre l’exercice est d’identifier les paramètres de la distribution hypergéométrique. Dans ce cas, le nombre total d’éléments dans la population est de 50 ( N =50), le nombre maximum de cas favorables est de 20 ( K =20), et on tire 12 boules ( n =12).

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

Nous voulons calculer la probabilité de tirer 4 boules bleues ( x =4), nous appliquons donc la formule de distribution hypergéométrique, substituons les variables par leurs valeurs correspondantes et effectuons le calcul :

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

Calculateur de distribution hypergéométrique

Entrez les paramètres de la distribution hypergéométrique dans le calculateur en ligne suivant pour calculer la probabilité d’occurrence de l’événement souhaité.

N’oubliez pas que N est la taille de la population, K est le nombre total de cas favorables, n est la taille de l’échantillon et x est la valeur pour laquelle nous voulons trouver la probabilité que cela se produise.

Caractéristiques de la distribution hypergéométrique

La distribution hypergéométrique a les propriétés suivantes :

La valeur attendue d’une distribution hypergéométrique est égale au nombre d’éléments dans l’échantillon multiplié par le nombre total de cas favorables divisé par le nombre d’éléments dans la population.

$E[X]=\cfrac{n\cdot K}{N}$

Le mode d’une distribution hypergéométrique est la valeur arrondie à l’inférieur du produit de n+1 fois K+1 divisé par N+2 .

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

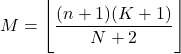
La variance d’une distribution hypergéométrique peut être obtenue à l’aide de l’expression suivante :

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

La fonction génératrice de moment d’une distribution hypergéométrique est la suivante :

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

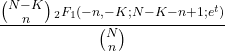
La fonction caractéristique de la distribution hypergéométrique est la suivante :

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

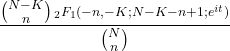
La probabilité d’occurrence d’un nombre donné d’événements peut être calculée à partir de la probabilité du nombre précédent en utilisant la formule récursive de la distribution hypergéométrique :

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

Distribution hypergéométrique et distribution binomiale

La différence entre la distribution hypergéométrique et la distribution binomiale est le remplacement. La distribution hypergéométrique est utilisée lorsque les extractions ne sont pas remplacées, cependant, dans la distribution binomiale, les extractions sont remplacées.

Par exemple, si nous tirons cinq cartes au hasard dans un jeu et que nous voulons calculer la probabilité d’obtenir une certaine carte, si nous ne remplaçons pas chaque carte que nous piochons, nous devons utiliser la distribution hypergéométrique pour effectuer le calcul. Mais si lors du retrait d’une carte nous la remettons avant d’effectuer l’extraction suivante, alors nous devons utiliser la distribution binomiale pour calculer la probabilité.

Lorsque le nombre N est grand, le rapport n/N est petit et le nombre de cas favorables souhaités est très faible, on peut utiliser la distribution hypergéométrique comme approximation de la distribution binomiale. Cependant, je ne le recommande pas car le résultat ne sera pas aussi fiable et, de plus, il est plus facile de calculer des probabilités avec la loi binomiale qu’avec la loi hypergéométrique.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus