Distribution lognormale
Cet article explique ce qu’est la distribution lognormale dans les statistiques. Ainsi, vous découvrirez quelles sont les propriétés de la distribution lognormale et le graphique de ce type de distribution de probabilité.
Quelle est la distribution lognormale ?
La distribution lognormale , ou distribution lognormale , est une distribution de probabilité qui définit une variable aléatoire dont le logarithme suit une distribution normale.
Par conséquent, si la variable X a une distribution normale, alors la fonction exponentielle e x a une distribution lognormale.
Notez que la distribution lognormale ne peut être utilisée que lorsque les valeurs des variables sont positives, puisque le logarithme est une fonction qui ne prend qu’un seul argument positif.
Parmi les différentes applications de la distribution lognormale, en statistique, on distingue l’utilisation de cette distribution pour analyser les investissements financiers et réaliser des analyses de fiabilité.
La distribution lognormale est également connue sous le nom de distribution Tinaut , parfois également écrite sous le nom de distribution lognormale ou de distribution log-normale .
Tracé de la distribution lognormale
Maintenant que nous connaissons la définition de la distribution lognormale, nous verrons dans cette section comment la représentation graphique de la distribution lognormale varie en fonction des valeurs de sa moyenne arithmétique et de son écart type.
Le graphique de la fonction de densité de la distribution lognormale est le suivant :
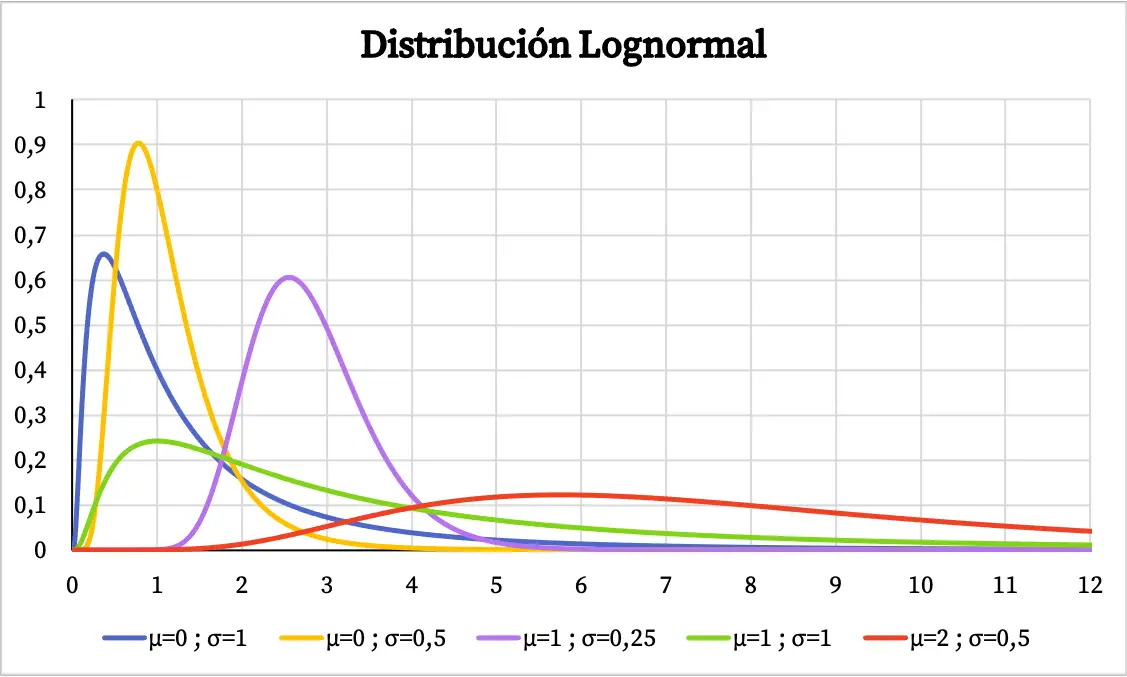
D’autre part, le graphique de la probabilité cumulée de la distribution lognormale est le suivant :
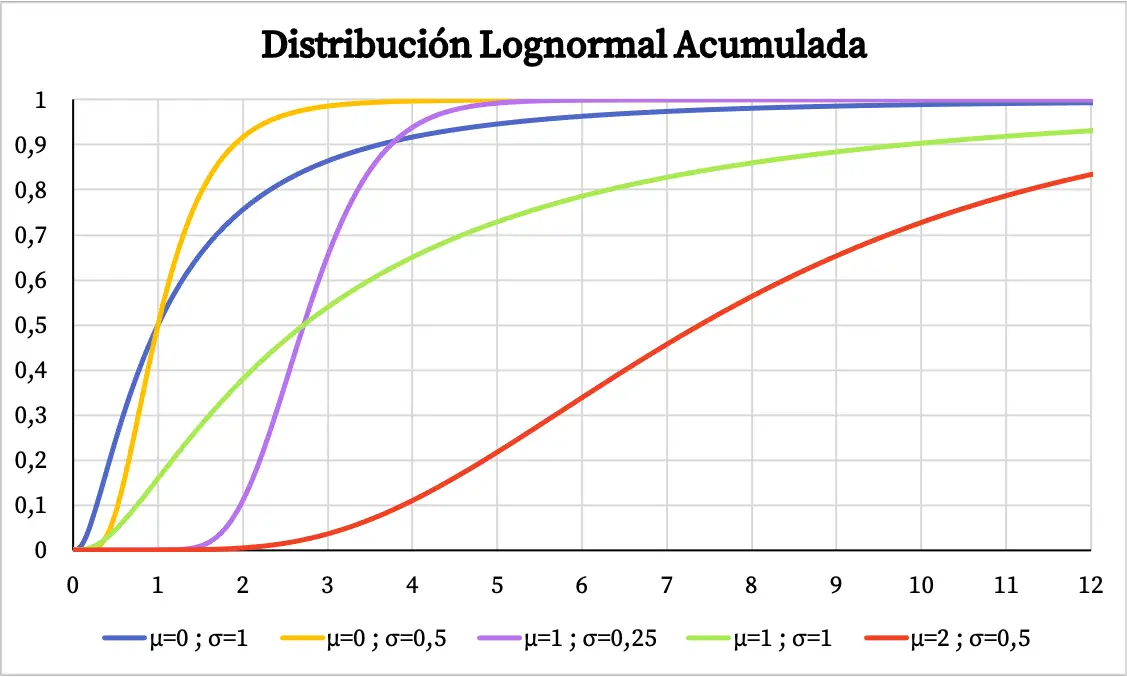
Caractéristiques de la distribution lognormale
La distribution lognormale présente les caractéristiques suivantes :
- La distribution lognormale est définie par la valeur de deux paramètres, sa moyenne arithmétique μ et sa variance σ 2 .
- Le domaine de la distribution lognormale est constitué de nombres réels positifs, car le logarithme n’accepte pas de valeurs négatives ou nulles.
- L’espérance d’une distribution lognormale est égale au nombre e élevé à la somme de la moyenne plus la variance divisée par deux.
![\displaystyle E[X]=e^{\mu+\frac{\sigma^2}{2}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-109a1024d530b2993db41f1d7a5a24c3_l3.png "Rendered by QuickLaTeX.com")
- D’autre part, la variance d’une distribution lognormale peut être calculée avec l’expression suivante :
- Le mode de la distribution lognormale est équivalent au nombre e élevé à la moyenne de la distribution.
- Le coefficient d’asymétrie de la distribution lognormale peut être déterminé en appliquant la formule suivante :
- La formule de la fonction de densité de la distribution lognormale est la suivante :
![\displaystyle P[X=x]=\frac{1}{\sigma \cdot x\cdot \sqrt{2 \pi}}\cdot \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)](https://statorials.org/wp-content/ql-cache/quicklatex.com-25698732745689402d16ea353a072cc1_l3.png "Rendered by QuickLaTeX.com")
- La formule de la fonction de probabilité cumulative de la distribution lognormale est la suivante :
![\displaystyle P[X\leq x]=\Phi\left(\frac{\ln x-\mu}{\sigma}\right)](https://statorials.org/wp-content/ql-cache/quicklatex.com-59c2474703bad4805a6a44bd05cf92bd_l3.png "Rendered by QuickLaTeX.com")
Où
est la fonction de probabilité cumulative d’une distribution normale standard .
- La moyenne arithmétique d’une distribution lognormale est supérieure à la valeur de sa médiane.
à propos de l'auteur
Pr Amélia Rodriguez
En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus