Une introduction à la distribution multinomiale

La distribution multinomiale décrit la probabilité d’obtenir un nombre spécifique de décomptes pour k résultats différents, lorsque chaque résultat a une probabilité fixe de se produire.

Si une variable aléatoire X suit une distribution multinomiale, alors la probabilité que le résultat 1 se produise exactement x ₁ fois, le résultat 2 se produise exactement x ₂ fois, le résultat 3 se produise exactement x ₃ fois, etc. peut être trouvée par la formule suivante :

Probabilité = n ! * (p ₁ ^{x ₁} * p ₂ ^{x ₂} * … * p _k ^{x _k} ) / (x ₁ ! * x ₂ ! … * x _k !)

où:

• n : nombre total d’événements
• x ₁ : nombre de fois où le résultat 1 se produit
• p ₁ : probabilité que le résultat 1 se produise dans un essai donné

Par exemple, supposons qu’il y ait 5 billes rouges, 3 billes vertes et 2 billes bleues dans une urne. Si l’on tire au hasard 5 billes de l’urne, avec remise, quelle est la probabilité d’obtenir exactement 2 billes rouges, 2 billes vertes et 1 bille bleue ?

Pour répondre à cette question, nous pouvons utiliser la distribution multinomiale avec les paramètres suivants :

• n : 5
• x ₁ (# billes rouges) = 2, x ₂ (# billes vertes) = 2, x ₃ (# billes bleues) = 1
• p ₁ (prob. rouge) = 0,5, p ₂ (prob. vert) = 0,3, p ₃ (prob. bleu) = 0,2

En insérant ces nombres dans la formule, nous trouvons que la probabilité est :

Probabilité = 5 ! * (.5 ² * .3 ² * .2 ¹ ) / (2! * 2! * 1!) = 0,135 .

Problèmes de pratique de distribution multinomiale

Utilisez les problèmes pratiques suivants pour tester vos connaissances de la distribution multinomiale.

Remarque : Nous utiliserons le calculateur de distribution multinomiale pour calculer les réponses à ces questions.

Problème 1

Question : Dans une élection à trois pour le maire, le candidat A reçoit 10 % des voix, le candidat B reçoit 40 % des voix et le candidat C reçoit 50 % des voix. Si nous sélectionnons un échantillon aléatoire de 10 électeurs, quelle est la probabilité que 2 aient voté pour le candidat A, 4 aient voté pour le candidat B et 4 aient voté pour le candidat C ?

Réponse : En utilisant le calculateur de distribution multinomiale avec les entrées suivantes, nous constatons que la probabilité est de 0,0504 :

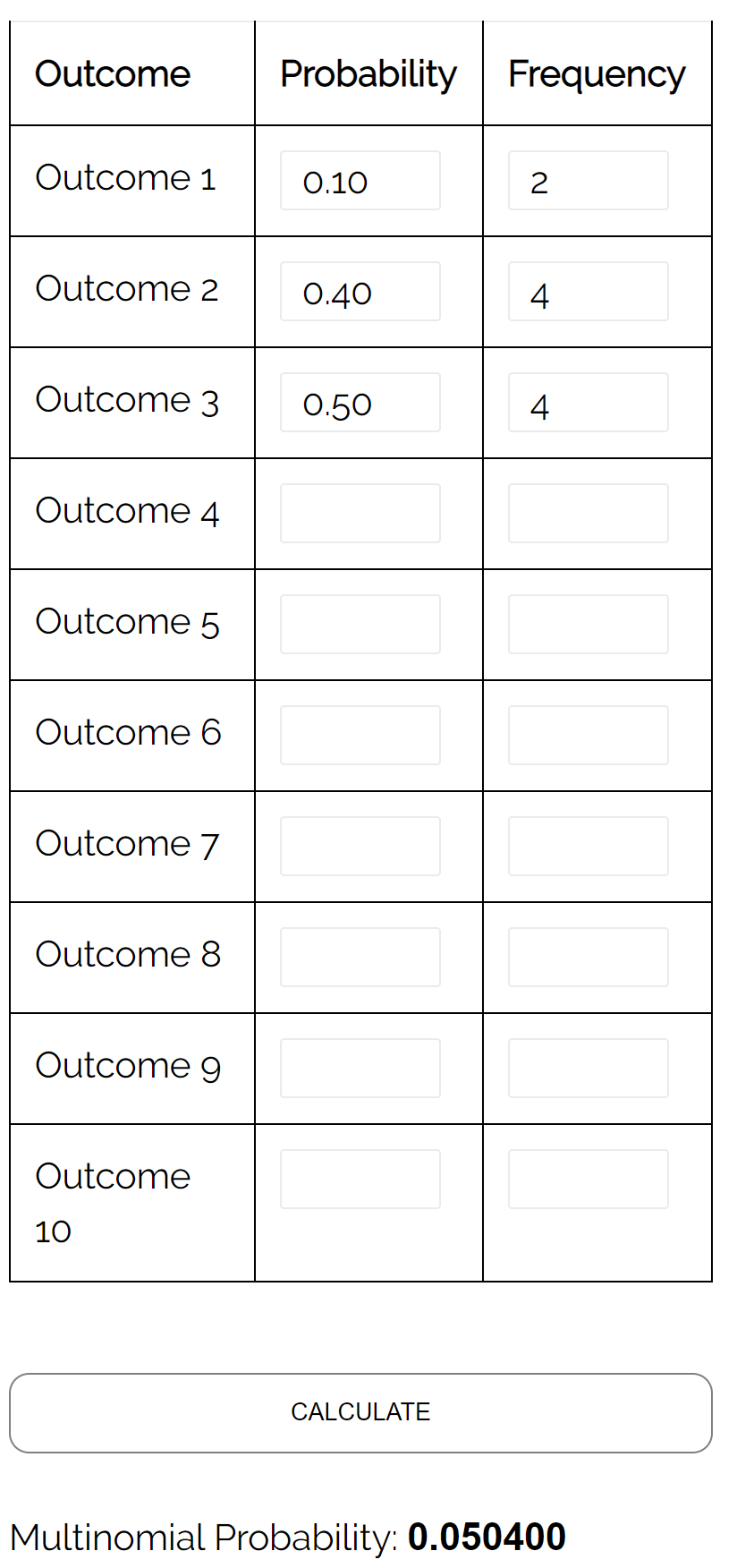
Problème 2

Question : Supposons qu’une urne contienne 6 billes jaunes, 2 billes rouges et 2 billes roses. Si nous sélectionnons au hasard 4 boules dans l’urne, avec remise, quelle est la probabilité que les 4 boules soient toutes jaunes ?

Réponse : En utilisant le calculateur de distribution multinomiale avec les entrées suivantes, nous constatons que la probabilité est de 0,1296 :

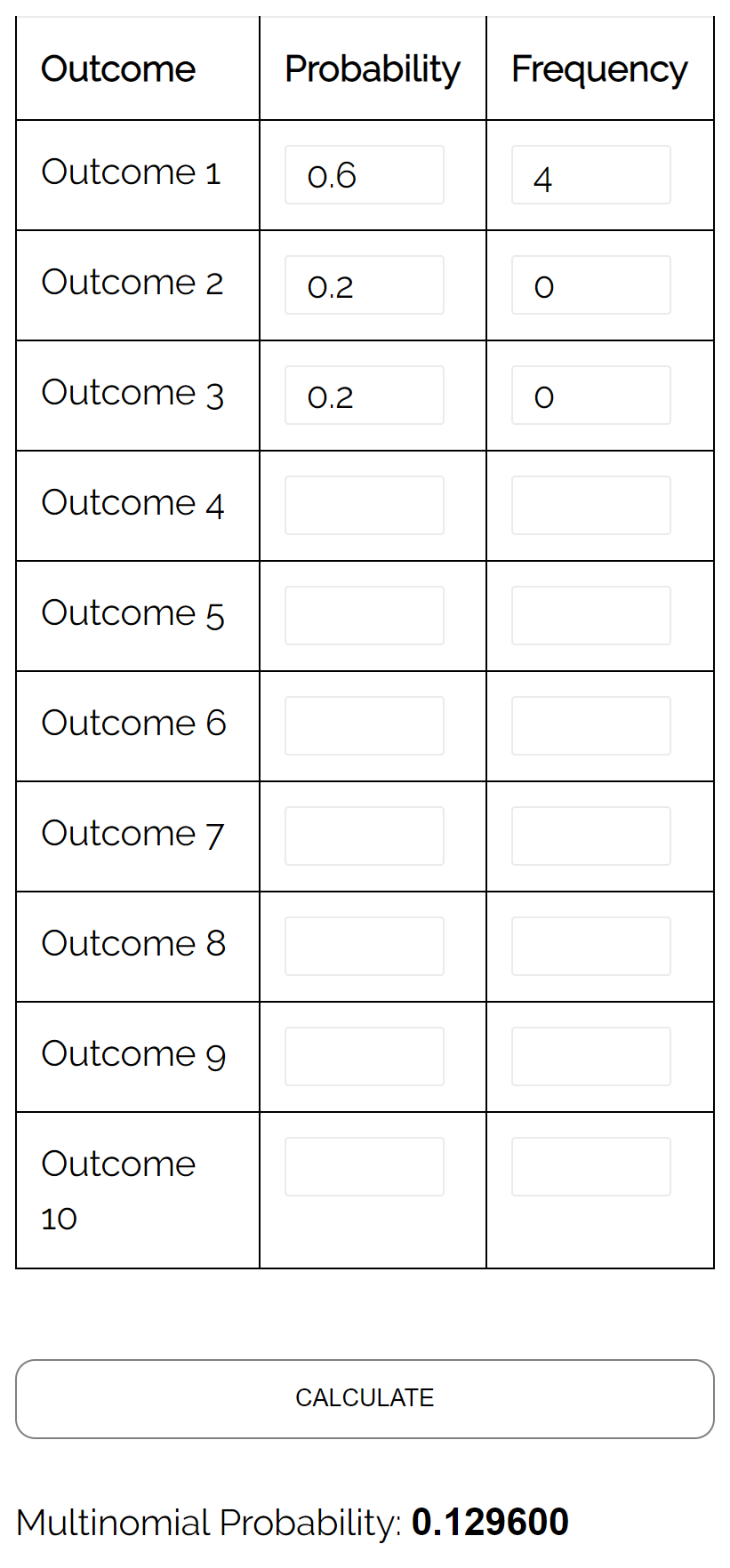
Problème 3

Question : Supposons que deux élèves jouent aux échecs l’un contre l’autre. La probabilité que l’élève A gagne un jeu donné est de 0,5, la probabilité que l’élève B gagne un jeu donné est de 0,3 et la probabilité qu’il y ait égalité dans un jeu donné est de 0,2. S’ils jouent 10 parties, quelle est la probabilité que le joueur A gagne 4 fois, le joueur B gagne 5 fois et qu’ils soient à égalité 1 fois ?

Réponse : En utilisant le calculateur de distribution multinomiale avec les entrées suivantes, nous constatons que la probabilité est de 0,038272 :

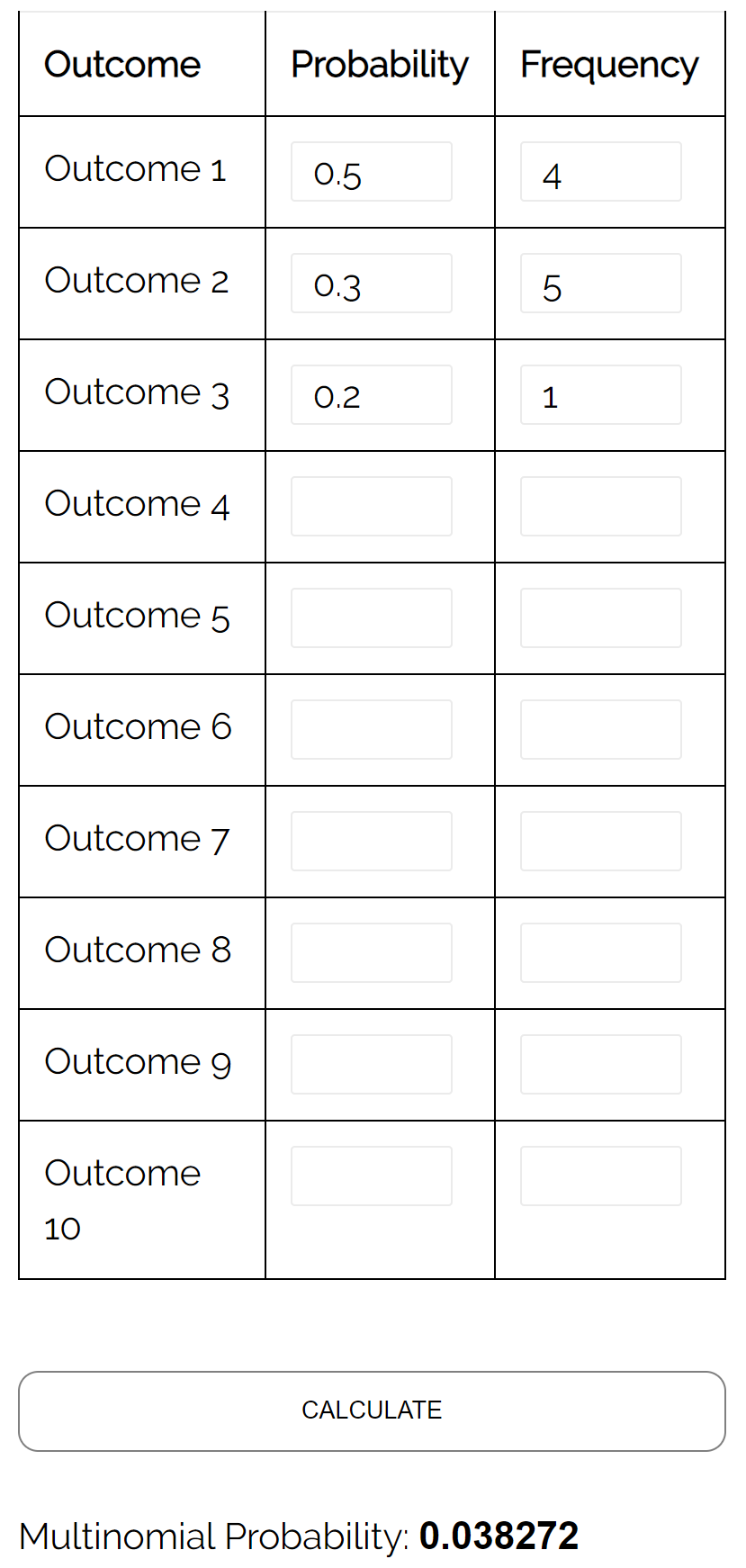
Ressources additionnelles

Les didacticiels suivants fournissent une introduction à d’autres distributions courantes dans les statistiques :

Une introduction à la distribution normale
Une introduction à la distribution binomiale
Une introduction à la distribution de Poisson
Une introduction à la distribution géométrique