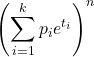Distribution multinomiale

Par Pr Amélia Rodriguez août 4, 2023 Probabilité 0 commentaire

Cet article explique ce qu’est une distribution multinomiale en statistiques. Ainsi, vous trouverez la définition d’une distribution multinomiale, quelle est sa formule, un exercice résolu et quelles sont les propriétés de ce type de distribution de probabilité. De plus, vous pourrez calculer la probabilité d’une distribution multinomiale avec un calculateur en ligne.

Qu’est-ce qu’une distribution multinomiale ?

La distribution multinomiale (ou distribution multinomiale ) est une distribution de probabilité qui décrit la probabilité que plusieurs événements mutuellement exclusifs se produisent un nombre de fois donné après plusieurs essais.

Autrement dit, si une expérience aléatoire peut aboutir à trois événements exclusifs ou plus et que la probabilité que chaque événement se produise séparément est connue, la distribution multinomiale est utilisée pour calculer la probabilité que lorsque plusieurs expériences sont réalisées, un certain nombre d’événements se produisent. fois à chaque fois.

La distribution multinomiale est donc une généralisation de la distribution binomiale.

Formule de distribution multinomiale

Pour calculer une probabilité de distribution multinomiale, vous devez d’abord déterminer le quotient entre la factorielle du nombre total de données et les factorielles du nombre d’occurrences de chaque événement, et le résultat est multiplié par le produit de la probabilité de chaque événement. porté au nombre d’occurrences dudit événement.

Autrement dit, la formule de la distribution multinomiale est la suivante :

Où:

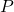$P$ est la probabilité de la distribution multinomiale calculée.
$n$ est le nombre total de tests effectués.
$x_i$ est le nombre de fois que l’événement se produit $i$ .
$p_i$ est la probabilité que l’événement se produise $i$ .

👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer la probabilité d’une variable qui suit la distribution multinomiale.

Exemple de distribution multinomiale

Pour finir de comprendre le concept de distribution multinomiale, vous avez résolu ci-dessous un exemple de calcul de la probabilité d’une distribution multinomiale.

Un magasin vend trois produits différents. Lorsqu’un client effectue un achat, la probabilité qu’il s’agisse du produit A, du produit B ou du produit C est respectivement de 30 %, 15 % et 55 %. Trouvez la probabilité que lorsque le magasin a vendu 8 unités, 2 soient du produit A, 1 du produit B et 5 du produit C.

Le problème défini est régi par une distribution multinomiale, il faut donc appliquer la formule de ce type de distribution de probabilité :

$P=\cfrac{n!}{x_1!\cdot x_2!\cdot x_3!}\cdot p_1^{x_1}\cdot p_2^{x_2}\cdot p_3^{x_3}$

Nous substituons donc les données du problème dans la formule et effectuons le calcul de probabilité :

$P=\cfrac{8!}{2!\cdot 1!\cdot 5!}\cdot 0,30^{2}\cdot 0,15^{1}\cdot 0,55^{5}=0,114$

Ainsi, la probabilité que ce que dit l’énoncé du problème se produise est de 11,4 %.

Calculateur de distribution multinomiale

Inscrivez le nombre d’occurrences de chaque événement dans la première case et, dans le même ordre, la probabilité d’occurrence de chaque événement dans la deuxième case. Saisissez ensuite le nombre total d’essais effectués dans le dernier espace vide.

Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Propriétés de la distribution multinomiale

La distribution multinomiale répond aux caractéristiques suivantes :

Dans une distribution multinomiale, la valeur attendue du nombre de fois où l’événement i se produit lors de l’exécution de n essais est égale au nombre total d’essais effectués multiplié par la probabilité que l’événement se produise.

$E[x_i]=n\cdot p_i$

Dans une distribution multinomiale, la variance pour l’événement i est calculée à l’aide de l’expression suivante :

$Var(x_i)=n\cdot p_i\cdot (1-p_i)$

De même, la covariance entre deux événements est équivalente au résultat du produit du nombre total d’essais multiplié par la probabilité de chaque événement multiplié par -1 :

$Cov(x_i,x_j)=-n\cdot p_i\cdot p_j\qquad i\neq j$

La fonction génératrice de moment pour une distribution multinomiale est :

$\displaystyle \left(\sum_{i=1}^k p_ie^{t_i}\right) ^n$

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus