Distribution normale

Par Pr Amélia Rodriguez août 3, 2023 Probabilité 0 commentaire

Cet article explique quelle est la distribution normale dans les statistiques. Ainsi, vous trouverez la définition de la distribution normale, des exemples de distributions normales et quelles sont les propriétés de la distribution normale.

Quelle est la distribution normale ?

La distribution normale est une distribution de probabilité continue dont le graphique est en forme de cloche et symétrique par rapport à sa moyenne. En statistique, la distribution normale est utilisée pour modéliser des phénomènes aux caractéristiques très différentes, c’est pourquoi cette distribution est si importante.

En fait, en statistique, la distribution normale est considérée de loin comme la distribution la plus importante de toutes les distributions de probabilité, car elle permet non seulement de modéliser un grand nombre de phénomènes réels, mais la distribution normale peut également être utilisée pour approximer d’autres types de distributions. sous certaines conditions.

Le symbole de la distribution normale est la lettre majuscule N. Ainsi, pour indiquer qu’une variable suit une distribution normale, elle est indiquée par la lettre N et les valeurs de sa moyenne arithmétique et de son écart type sont ajoutées entre parenthèses.

$X\sim N(\mu,\sigma)$

La distribution normale porte de nombreux noms différents, notamment distribution gaussienne , distribution gaussienne et distribution de Laplace-Gauss .

Exemples de distributions normales

En règle générale, les ensembles de données qui suivent une distribution normale contiennent un grand nombre d’observations et traitent de sujets très généraux. Vous trouverez ci-dessous plusieurs exemples d’échantillons statistiques qui peuvent généralement être modélisés avec une distribution normale.

Exemples de distribution normale :

La taille des étudiants dans un cours.
Le QI des travailleurs d’une entreprise.
Le nombre de pièces défectueuses produites dans une usine pendant une journée.
Les notes obtenues à un examen par les étudiants d’un cours.
La rentabilité des actions de sociétés cotées en bourse.

Graphique de distribution normale

Une fois que nous avons vu en quoi consiste la distribution normale et quelques exemples de ce type de distribution de probabilité, voyons à quoi ressemble son graphique pour mieux comprendre le concept.

Dans le graphique suivant, vous pouvez voir comment la fonction de densité de la distribution normale varie en fonction des valeurs de sa moyenne arithmétique et de son écart type.

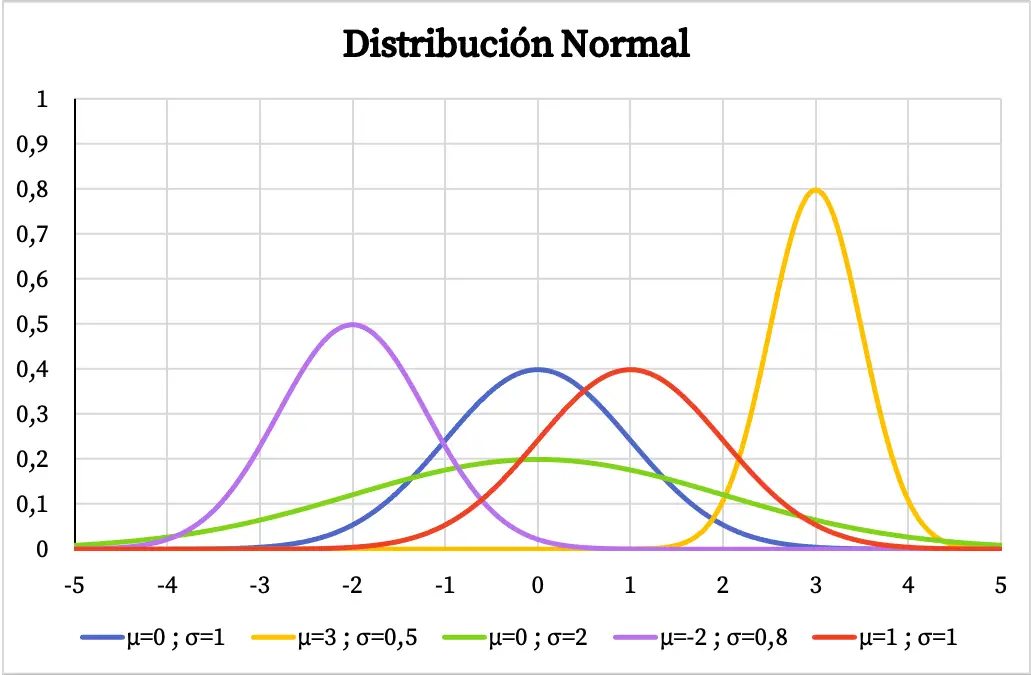
Ayant une forme de cloche centrée sur la moyenne arithmétique, si une variable a une distribution normale cela signifie que la valeur la plus répétée est la moyenne et que les valeurs autour de la moyenne se répètent plus fréquemment que les valeurs extrêmes. De même, plus l’écart type de la distribution normale est grand, plus la forme de sa représentation graphique est plate.

D’autre part, le graphique de la fonction de probabilité cumulée de la distribution normale dépend également des valeurs de sa moyenne arithmétique et de son écart type, comme vous pouvez le voir sur l’image suivante :

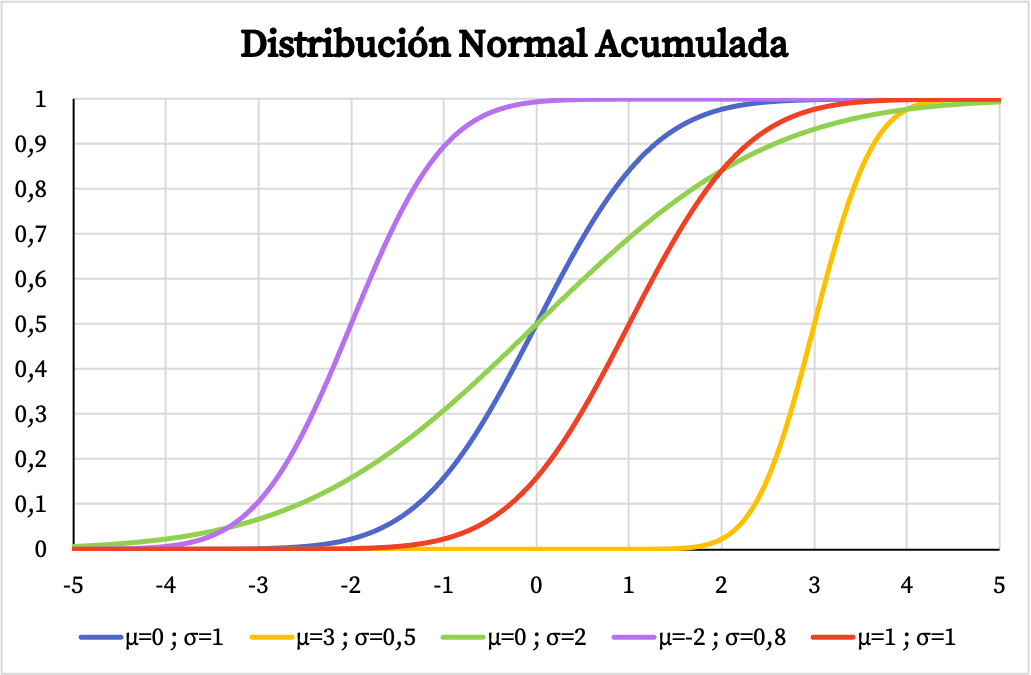
graphique de la fonction de probabilité cumulative de la distribution normale

La fonction de densité et la fonction de distribution de la distribution normale permettent de calculer des probabilités liées à cette distribution. Cependant, au lieu d’utiliser leurs formules, vous pouvez utiliser directement les tables de distribution normales car c’est plus rapide. Vous pouvez consulter ces tableaux sur le lien suivant :

➤ Voir : Tableau de distribution normale

Caractéristiques de la distribution normale

La distribution normale a les caractéristiques suivantes :

La distribution normale dépend de deux paramètres caractéristiques, qui sont sa moyenne arithmétique (μ) et son écart type (σ).

$X\sim N(\mu,\sigma)$

La distribution normale peut prendre des valeurs positives et négatives, donc le domaine de la distribution normale est constitué de nombres réels.

$x\in \mathbb{R}$

La médiane et le mode de la distribution normale sont égaux à la moyenne arithmétique de la distribution.

$Me=Mo=\mu$

Le coefficient d’asymétrie et le coefficient d’aplatissement de la distribution normale sont nuls.

$\begin{array}{c}A=0\\[2ex]C=0\end{array}$

La formule de la fonction de densité de la distribution normale est la suivante :

$\displaystyle P[X=x]=\frac1{\sigma\sqrt{2\pi}}\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}}$

De même, la formule de la fonction de probabilité cumulative de la distribution normale est la suivante :

$\displaystyle P[X\leq x]=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{(x - \mu)^2}{2\sigma^2}}\, dx ,\quad x\in\mathbb{R}$

Une application du théorème central limite est qu’une distribution de Poisson peut se rapprocher d’une distribution normale lorsque la valeur de λ est suffisamment grande.

$\text{Poisson}(\lambda)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(\lambda, \sqrt{\lambda}\right)$

Une autre application du théorème central limite est qu’une distribution binomiale peut être approximée par une distribution normale pour des ensembles de données comportant un grand nombre d’observations.

$\text{Bin}(n,p)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(n\cdot p, \sqrt{n\cdot p \cdot (1-p)}\right)$

Distribution normale standard

La distribution normale standard , également appelée distribution normale unitaire , est le cas le plus simple de distribution normale. Plus précisément, la distribution normale standard est une distribution normale avec des valeurs moyennes et d’écart type égales à 0 et 1 respectivement.

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

Il est à noter que toute distribution normale peut être transformée en distribution normale standard en appliquant un processus appelé typage, qui consiste à soustraire sa moyenne arithmétique à chaque valeur puis à diviser par son écart type.

De plus, la distribution normale standard est utilisée pour déterminer toute probabilité d’une distribution normale à l’aide de sa table de probabilité. Ainsi, pour trouver une probabilité d’une distribution normale, la variable est d’abord saisie pour la convertir en une distribution normale standard et, ensuite, nous regardons dans le tableau quelle est la valeur de la probabilité correspondante. Pour en savoir plus, cliquez sur le lien suivant :

➤ Voir : Distribution normale standard

La distribution normale et la règle empirique

En statistiques, la règle empirique , également appelée règle 68-95-99,7 , est une règle qui définit le pourcentage de valeurs dans une distribution normale qui se situent à moins de trois écarts types de la moyenne.

Plus précisément, la règle empirique stipule ce qui suit :

68 % des valeurs d’une distribution normale se situent à moins d’un écart type de la moyenne.
95 % des valeurs d’une distribution normale se situent à moins de deux écarts types de la moyenne.
99,7 % des valeurs d’une distribution normale se situent à moins de trois écarts types de la moyenne.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus