Distribution normale inverse : définition & Exemple

Le terme distribution normale inverse fait référence à la méthode consistant à utiliser une probabilité connue pour trouver la valeur z-critique correspondante dans une distribution normale .

Cela ne doit pas être confondu avec la distribution gaussienne inverse , qui est une distribution de probabilité continue.

Ce didacticiel fournit plusieurs exemples d’utilisation de la distribution normale inverse dans différents logiciels statistiques.

Distribution normale inverse sur une calculatrice TI-83 ou TI-84

Vous êtes plus susceptible de rencontrer le terme « distribution normale inverse » sur une calculatrice TI-83 ou TI-84, qui utilise la fonction suivante pour trouver la valeur z critique qui correspond à une certaine probabilité :

invNorm(probabilité, μ, σ)

où:

• probabilité : le niveau de signification
• μ : moyenne de la population
• σ : écart type de la population

Vous pouvez accéder à cette fonction sur une calculatrice TI-84 en appuyant sur 2nd puis en appuyant sur vars . Cela vous amènera à un écran DISTR où vous pourrez ensuite utiliser invNorm() :

Par exemple, nous pouvons utiliser cette fonction pour trouver la valeur z-critique qui correspond à une valeur de probabilité de 0,05 :

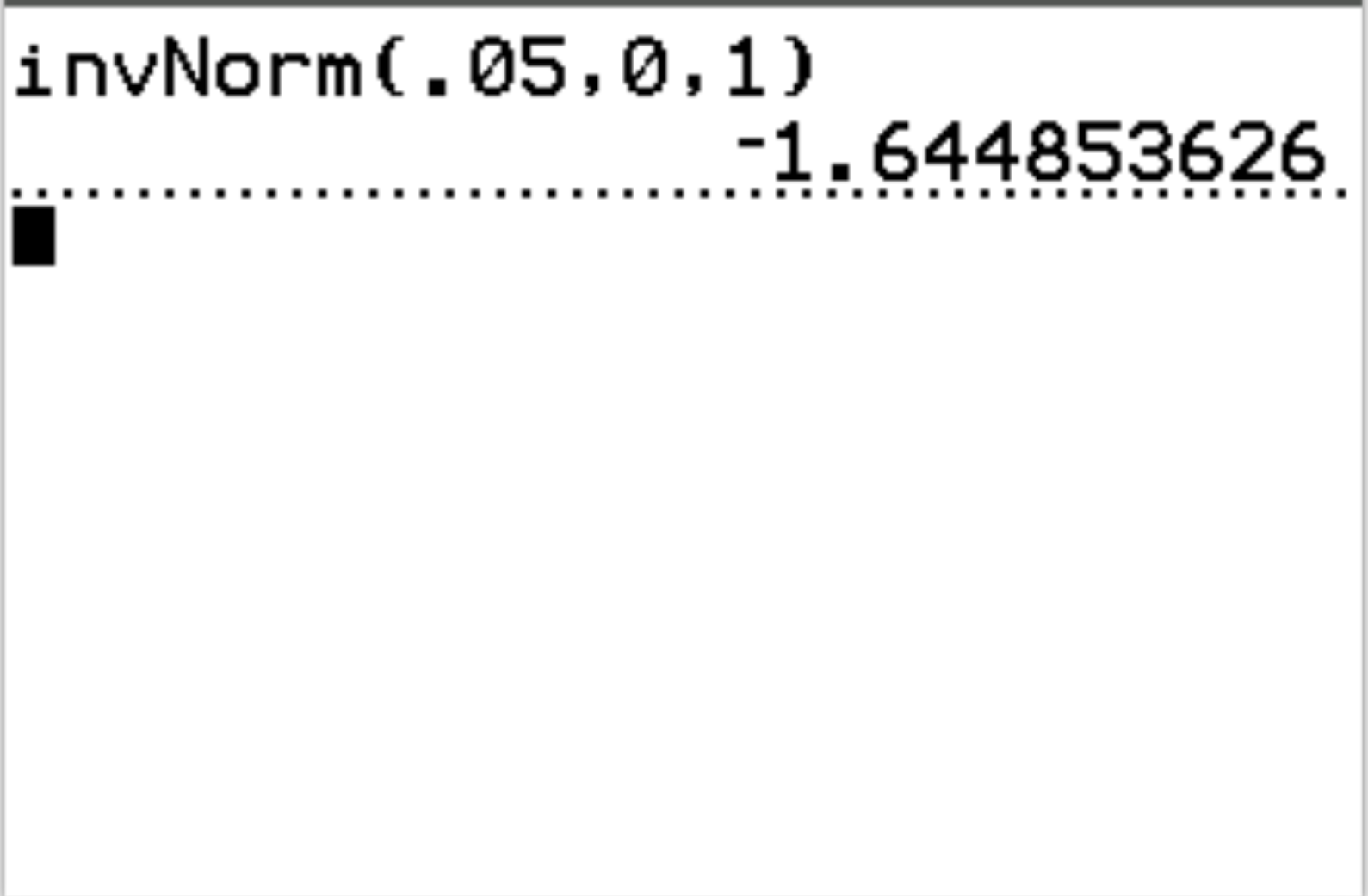
La valeur critique z qui correspond à une valeur de probabilité de 0,05 est -1,64485 .

Connexe : Comment utiliser invNorm sur une calculatrice TI-84 (avec exemples)

Distribution normale inverse dans Excel

Pour trouver la valeur z-critique associée à une certaine valeur de probabilité dans Excel, nous pouvons utiliser la fonction INVNORM() , qui utilise la syntaxe suivante :

INVNORM(p, moyenne, sd)

où:

• p : le niveau de signification
• moyenne : moyenne de la population
• sd : écart type de la population

Par exemple, nous pouvons utiliser cette fonction pour trouver la valeur z-critique qui correspond à une valeur de probabilité de 0,05 :

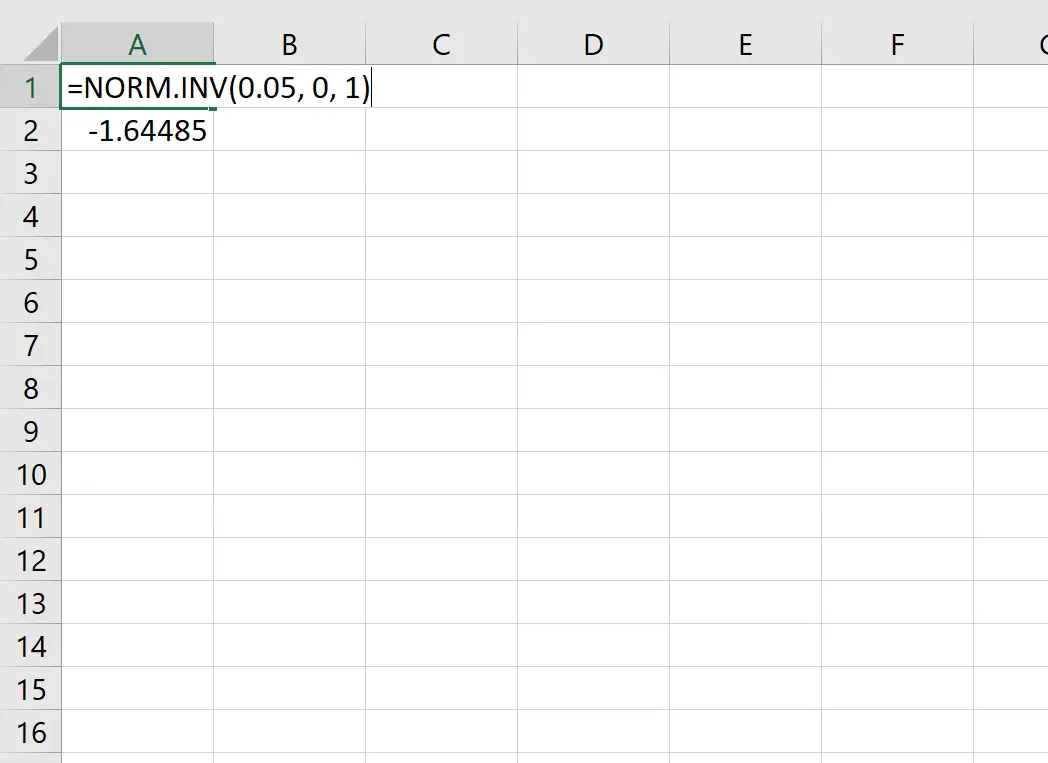
La valeur critique z qui correspond à une valeur de probabilité de 0,05 est -1,64485 .

Distribution normale inverse dans R

Pour trouver la valeur z-critique associée à une certaine valeur de probabilité dans R, nous pouvons utiliser la fonction qnorm() , qui utilise la syntaxe suivante :

qnorme (p, moyenne, sd)

où:

• p : le niveau de signification
• moyenne : moyenne de la population
• sd : écart type de la population

Par exemple, nous pouvons utiliser cette fonction pour trouver la valeur z-critique qui correspond à une valeur de probabilité de 0,05 :

qnorm(p=.05, mean=0, sd=1)

[1] -1.644854

Encore une fois, la valeur z-critique qui correspond à une valeur de probabilité de 0,05 est -1,64485 .