Distribution normale et distribution normale standard : la différence

La distribution normale est la distribution de probabilité la plus couramment utilisée en statistique.

Il possède les propriétés suivantes :

• Symétrique
• En forme de cloche
• La moyenne et la médiane sont égales ; tous deux situés au centre de la distribution

La moyenne de la distribution normale détermine son emplacement et l’écart type détermine sa propagation.

Par exemple, le graphique suivant montre trois distributions normales avec des moyennes et des écarts types différents :

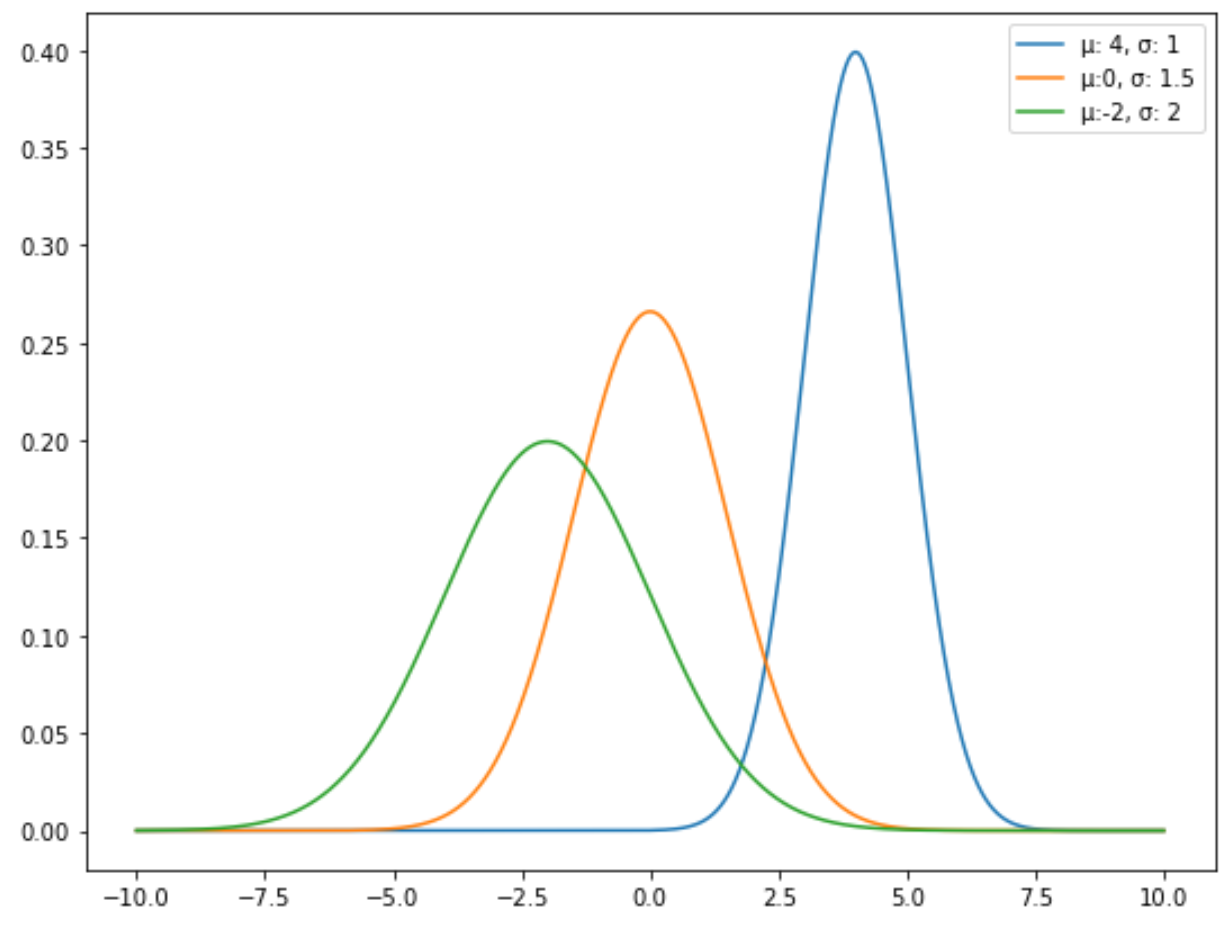
La distribution normale standard est un type spécifique de distribution normale où la moyenne est égale à 0 et l’écart type est égal à 1.

Le graphique suivant montre une distribution normale standard :

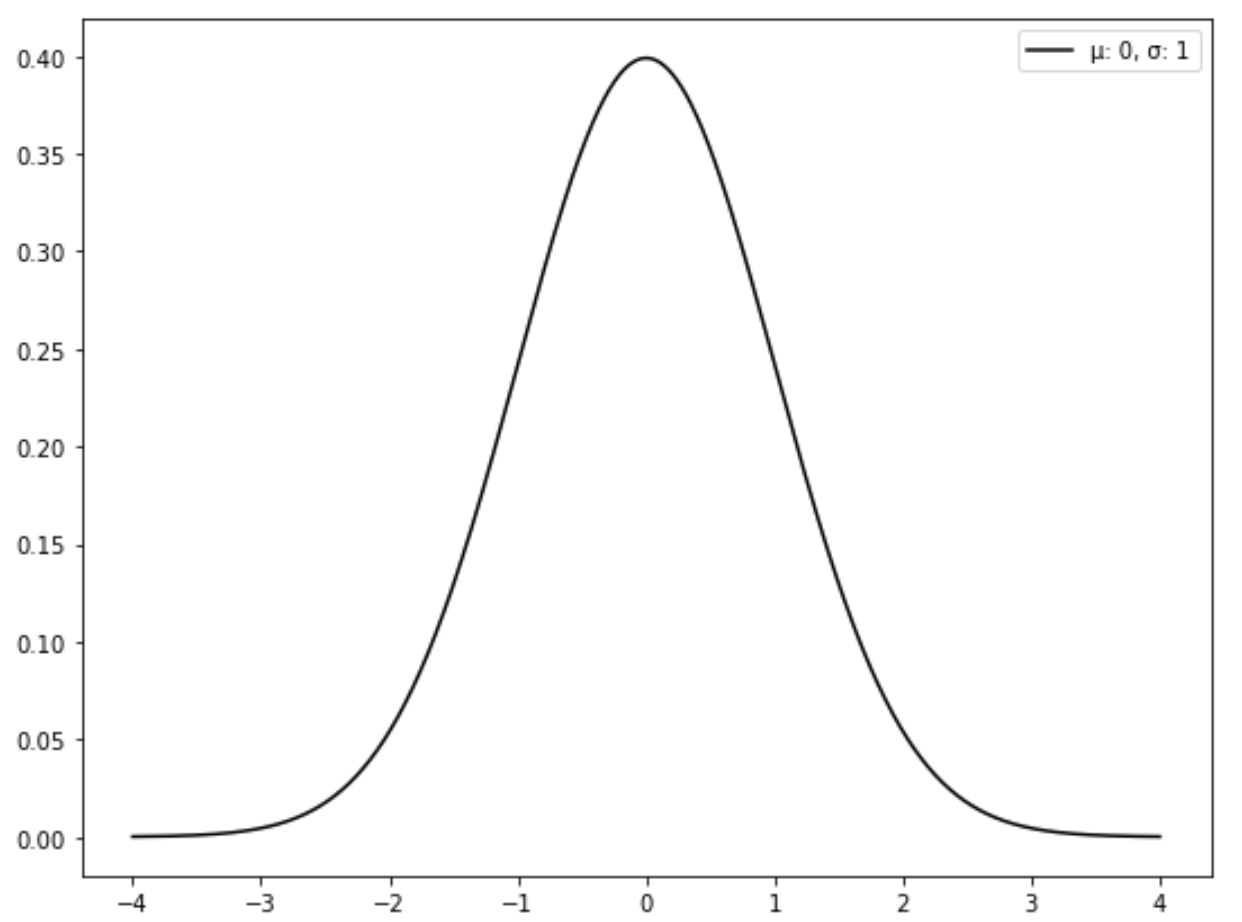
Comment convertir une distribution normale en distribution normale standard

Toute distribution normale peut être convertie en distribution normale standard en convertissant les valeurs des données en scores z, à l’aide de la formule suivante :

z = (x – μ) / σ

où:

• x : valeur des données individuelles
• μ : Moyenne de la distribution
• σ : Écart type de la distribution

Par exemple, supposons que nous ayons l’ensemble de données suivant avec une moyenne de 6 et un écart type de 2,152 :

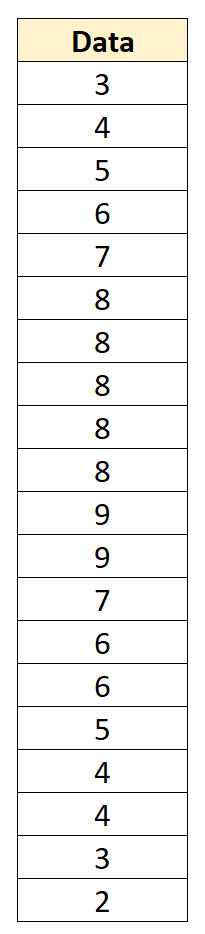
Nous pouvons convertir chaque valeur de données individuelle en un score z en soustrayant 6 de chaque valeur et en divisant par 2,152 :

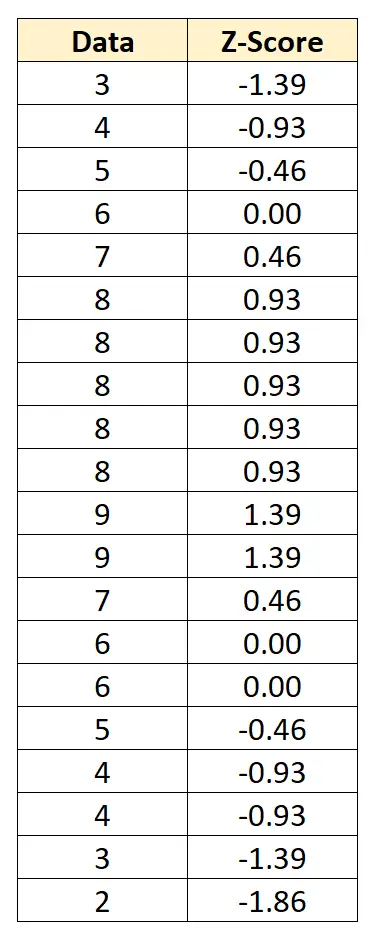
Le score z nous indique à combien d’écarts types chaque point de données se trouve par rapport à la moyenne. Par exemple, la première valeur de données « 3 » se situe à 1,39 écart-type en dessous de la moyenne.

La moyenne de cette distribution des scores z a une moyenne de zéro et un écart type de un.

Comment utiliser la distribution normale standard

Une distribution normale standard a les propriétés suivantes :

• Environ 68 % des données se situent dans un écart type de la moyenne
• Environ 95 % des données se situent à moins de deux écarts types de la moyenne.
• Environ 99,7 % des données se situent dans une fourchette de trois écarts types par rapport à la moyenne.

Ceci est connu sous le nom de règle empirique et est utilisé pour comprendre la distribution des valeurs dans un ensemble de données.

Par exemple, supposons que la hauteur des plantes dans un certain jardin soit normalement distribuée avec une moyenne de 47,4 pouces et un écart type de 2,4 pouces.

Selon la règle empirique, quel pourcentage de plantes mesurent moins de 54,6 pouces de hauteur ?

La règle empirique stipule que pour un ensemble de données donné avec une distribution normale, 99,7 % des valeurs des données se situent dans trois écarts types de la moyenne. Cela signifie que 49,85 % des valeurs se situent entre la moyenne et trois écarts types au-dessus de la moyenne.

Dans cet exemple, 54,6 se situe trois écarts types au-dessus de la moyenne. Puisque nous savons que 50 % des valeurs des données sont inférieures à la moyenne dans une distribution normale, un total de 50 % + 49,85 % = 99,85 % des valeurs sont inférieures à 54,6.

Ainsi, 99,85 % des plantes mesurent moins de 54,6 pouces de hauteur.

Ressources additionnelles

Problèmes de pratique des règles empiriques
Calculateur de règles empiriques
Comment appliquer la règle empirique dans Excel