Distribution normale et distribution t : quelle est la différence ?
Ladistribution normale est la distribution la plus couramment utilisée dans toutes les statistiques et est connue pour être symétrique et en forme de cloche.
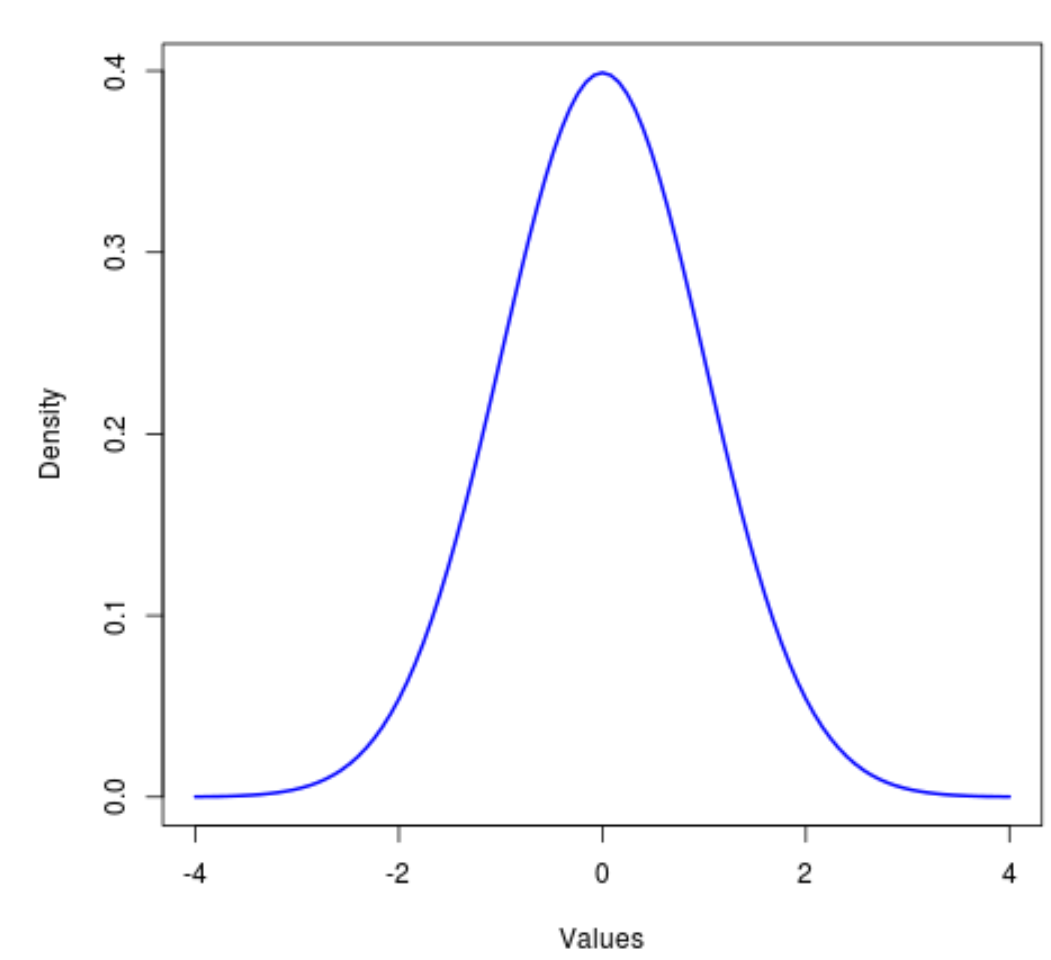
Une distribution étroitement liée est la distribution t , qui est également symétrique et en forme de cloche mais elle a des « queues » plus lourdes que la distribution normale.
Autrement dit, plus de valeurs dans la distribution sont situées aux extrémités que dans le centre par rapport à la distribution normale :
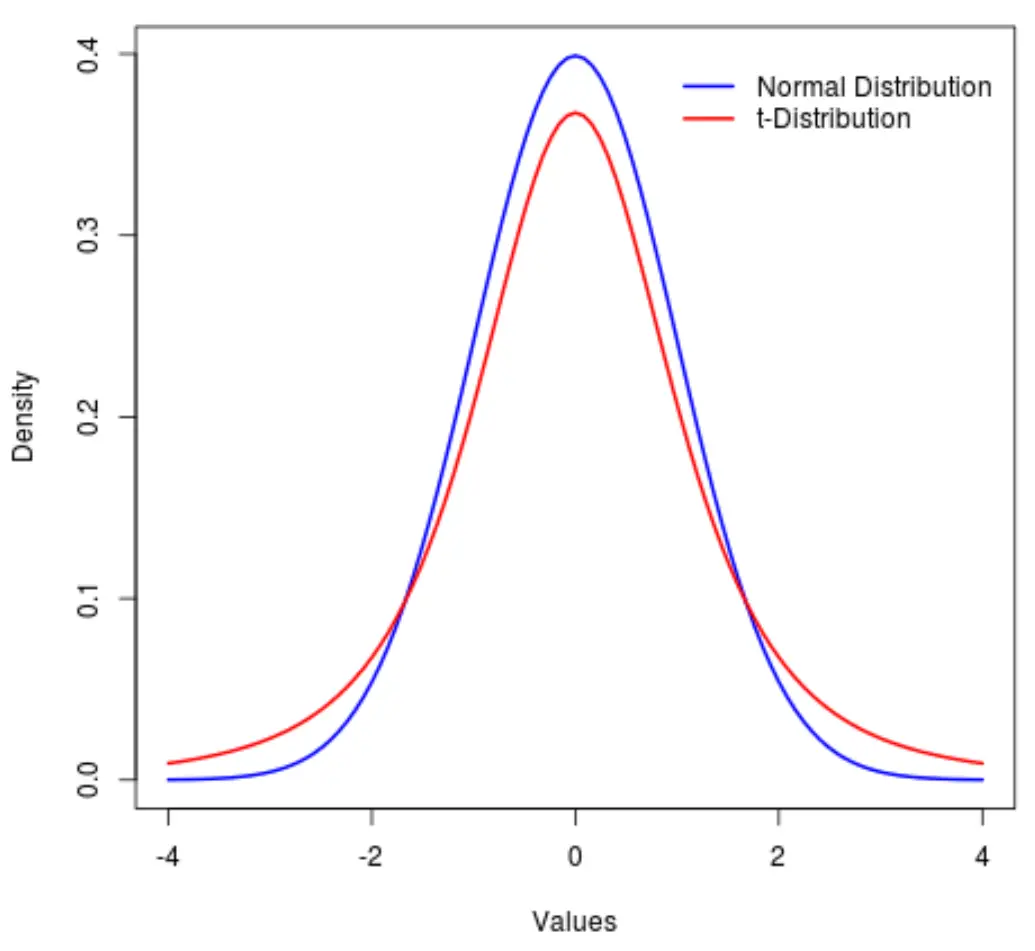
Dans le jargon statistique, nous utilisons une métrique appelée kurtosis pour mesurer le degré de « lourdeur » d’une distribution. Ainsi, nous dirions que l’aplatissement d’une distribution t est supérieur à celui d’une distribution normale.
En pratique, nous utilisons le plus souvent la distribution t lors de la réalisation de tests d’hypothèses ou de la construction d’intervalles de confiance .
Par exemple, la formule permettant de calculer un intervalle de confiance pour une moyenne de population est la suivante :
Intervalle de confiance = x +/- t 1-α/2, n-1 *(s/√ n )
où:
- x : moyenne de l’échantillon
- t : la valeur t critique, basée sur le niveau de signification α et la taille de l’échantillon n
- s : écart type de l’échantillon
- n : taille de l’échantillon
Dans cette formule, nous utilisons la valeur critique de latable t au lieu de la valeur critique de la table z lorsque l’une des conditions suivantes est vraie :
- Nous ne connaissons pas l’écart type de la population.
- La taille de l’échantillon est inférieure ou égale à 30.
L’organigramme suivant fournit un moyen utile de savoir si vous devez utiliser la valeur critique de la table t ou de la table z :

La principale différence entre l’utilisation de la distribution t et celle de la distribution normale lors de la construction d’intervalles de confiance est que les valeurs critiques de la distribution t seront plus grandes, ce qui conduit à des intervalles de confiance plus larges .
Par exemple, supposons que nous souhaitions construire un intervalle de confiance de 95 % pour le poids moyen d’une population de tortues, afin de collecter un échantillon aléatoire de tortues avec les informations suivantes :
- Taille de l’échantillon n = 25
- Poids moyen de l’échantillon x = 300
- Écart type de l’échantillon s = 18,5
La valeur critique z pour un niveau de confiance de 95 % est de 1,96 tandis qu’une valeur critique t pour un intervalle de confiance de 95 % avec df = 25-1 = 24 degrés de liberté est de 2,0639 .
Ainsi, un intervalle de confiance à 95 % pour la moyenne de la population utilisant une valeur z-critique est :
IC à 95 % = 300 +/- 1,96*(18,5/√ 25 ) = [ 292,75 , 307,25]
Alors qu’un intervalle de confiance de 95 % pour la moyenne de la population utilisant une valeur t-critique est :
IC à 95 % = 300 +/- 2,0639*(18,5/√25) = [ 292,36 , 307,64]
Notez que l’intervalle de confiance avec la valeur t-critique est plus large.
L’idée ici est que lorsque nous avons de petites tailles d’échantillon, nous sommes moins sûrs de la véritable moyenne de la population, il est donc utile d’utiliser la distribution t pour produire des intervalles de confiance plus larges qui ont plus de chances de contenir la véritable moyenne de la population.
Visualisation des degrés de liberté pour la distribution t
Il convient de noter qu’à mesure que les degrés de liberté augmentent, la distribution t se rapproche de la distribution normale.
Pour illustrer cela, considérons le graphique suivant qui montre la forme de la distribution t avec les degrés de liberté suivants :
- df = 3
- df = 10
- df = 30
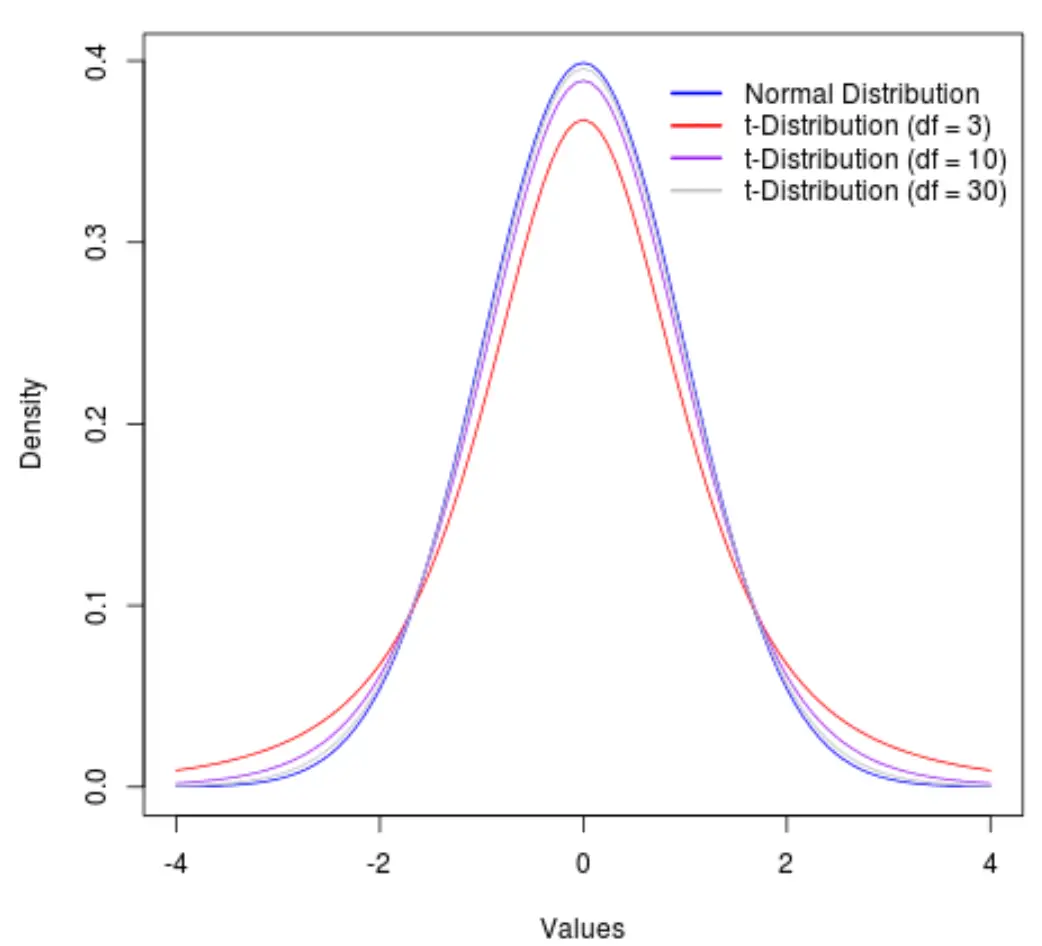
Au-delà de 30 degrés de liberté, la distribution t et la distribution normale deviennent si similaires que les différences entre l’utilisation d’une valeur t-critique et d’une valeur z-critique dans les formules deviennent négligeables.
