Distribution normale ou uniforme : quelle est la différence ?

La distribution normale est la distribution de probabilité la plus couramment utilisée en statistique.

Il possède les propriétés suivantes :

• Symétrique
• En forme de cloche

Si nous créons un tracé de la distribution normale, cela ressemblera à ceci :

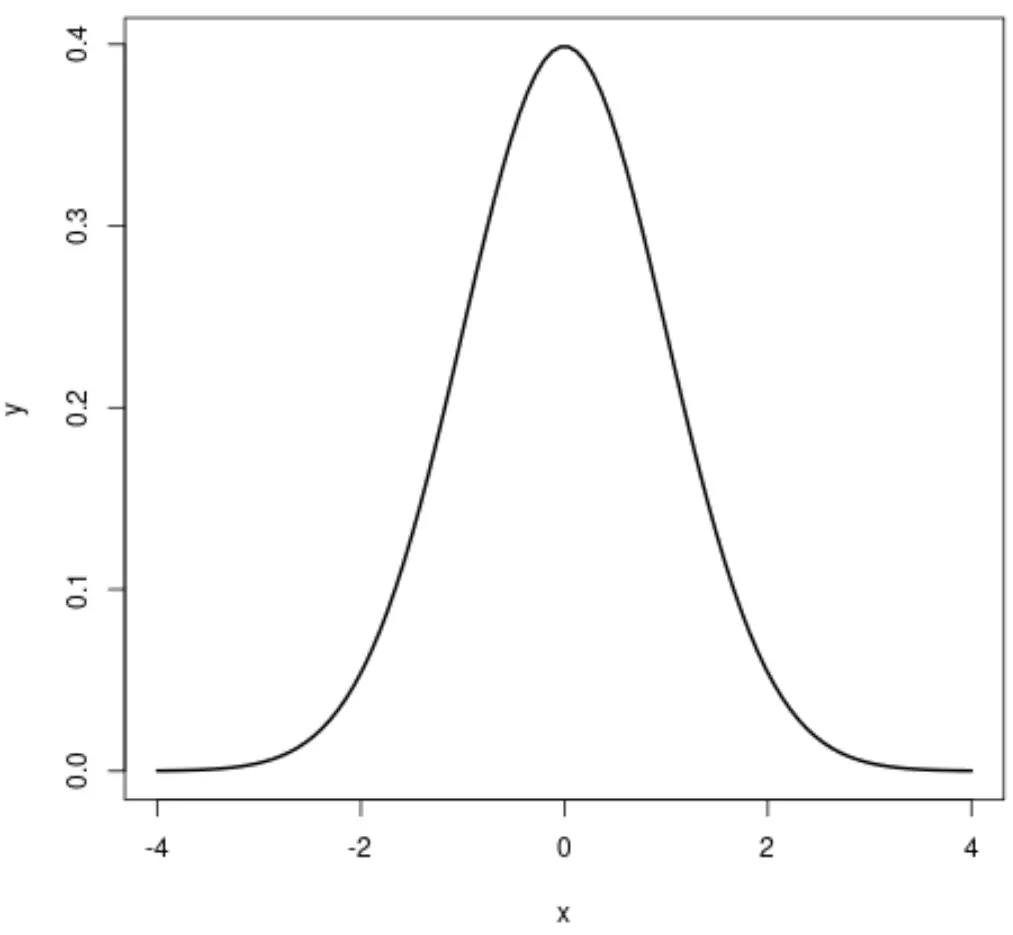
La distribution uniforme est une distribution de probabilité dans laquelle chaque valeur comprise entre un intervalle de a à b a la même probabilité de se produire.

Il possède les propriétés suivantes :

• Symétrique
• De forme rectangulaire

Si nous créons un tracé de la distribution uniforme, cela ressemblera à ceci :

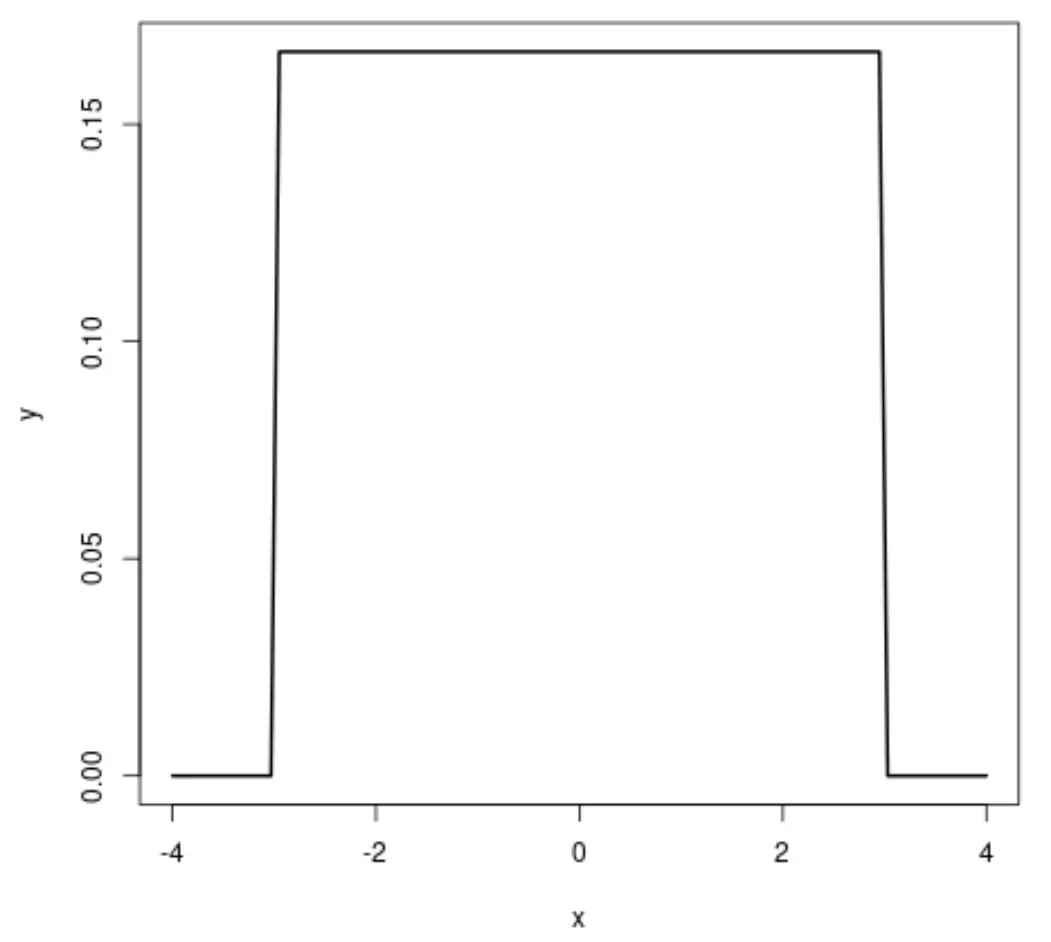
La distribution normale et la distribution uniforme partagent la similitude suivante :

• Les deux distributions sont symétriques. Autrement dit, si nous devions tracer une ligne au centre de la distribution, les côtés gauche et droit de la distribution se refléteraient parfaitement :

Cependant, les deux distributions présentent la différence suivante :

• Les distributions ont des formes différentes.
• La distribution normale est en forme de cloche, ce qui signifie que les valeurs proches du centre de la distribution sont plus susceptibles de se produire que les valeurs situées aux queues de la distribution.
• La distribution uniforme est de forme rectangulaire, ce qui signifie que chaque valeur de la distribution a la même probabilité de se produire.

Distribution normale ou distribution uniforme : quand les utiliser ?

La distribution normale est utilisée pour modéliser des phénomènes qui ont tendance à suivre une forme de « courbe en cloche ». Par exemple, il est bien documenté que le poids à la naissance des nouveau-nés est normalement réparti en moyenne autour de 7,5 livres.

L’histogramme du poids à la naissance des nouveau-nés aux États-Unis affiche une forme de cloche qui correspond généralement à la distribution normale :

La plupart des bébés pèsent probablement environ 7,5 livres, quelques-uns pesant moins de 7 livres et quelques-uns pesant plus de 8 livres.

À l’inverse, la distribution uniforme est utilisée pour modéliser des scénarios dans lesquels chaque résultat potentiel est également probable.

Un exemple classique est de lancer un dé. Si vous lancez un dé une fois, la probabilité qu’il tombe sur un nombre compris entre 1 et 6 suit une distribution uniforme car chaque nombre a la même probabilité d’apparaître.

Par exemple, il y a 6 nombres possibles sur lesquels le dé peut atterrir, donc la probabilité que vous obteniez un 1 est de 1/6.

De même, la probabilité que vous obteniez un 2 est de 1/6.

De même, la probabilité que vous obteniez un 3 est de 1/6.

Et ainsi de suite.

Bonus : Comment tracer la distribution normale et uniforme

Nous avons utilisé le code suivant dans R pour créer des tracés des distributions normales et uniformes :

#define x-axis
x <- seq(-4, 4, length=100)

#calculate normal distribution probabilities
y <- dnorm(x)

#plot normal distribution
plot(x, y, type = "l", lwd = 2)

#define x-axis
x <- seq(-4, 4, length=100)

#calculate uniform distribution probabilities
y <- dunif(x, min = -3, max = 3)

#plot uniform distribution
plot(x, y, type = "l", lwd = 2, xlim = c(-4, 4))

Ressources additionnelles

6 exemples concrets de la distribution normale
5 exemples concrets de distribution uniforme
Distribution symétrique : définition + exemples