Distribution t de Student
Cet article explique ce qu’est la distribution Student t et à quoi elle sert. De plus, le graphique de la distribution t de Student est affiché et quelles sont les caractéristiques de ce type de distribution de probabilité.
Quelle est la distribution t de Student ?
La distribution t de Student est une distribution de probabilité largement utilisée en statistique. Plus précisément, la distribution t de Student est utilisée dans le test t de Student pour déterminer la différence entre les moyennes de deux échantillons et pour établir des intervalles de confiance.
La distribution t de Student a été développée par le statisticien William Sealy Gosset en 1908 sous le pseudonyme de « Student ».
La distribution t de Student est définie par son nombre de degrés de liberté, obtenu en soustrayant une unité du nombre total d’observations. Par conséquent, la formule pour déterminer les degrés de liberté d’une distribution t de Student est ν=n-1 .
![\begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-1c805dc2d6ca050feb70dad99de53402_l3.png "Rendered by QuickLaTeX.com")
Graphique de la distribution t de Student
Maintenant que nous connaissons la définition de la distribution t de Student, voyons quel est son graphique. Ainsi, ci-dessous, vous pouvez voir graphiquement plusieurs exemples de distributions t de Student avec différents degrés de liberté.
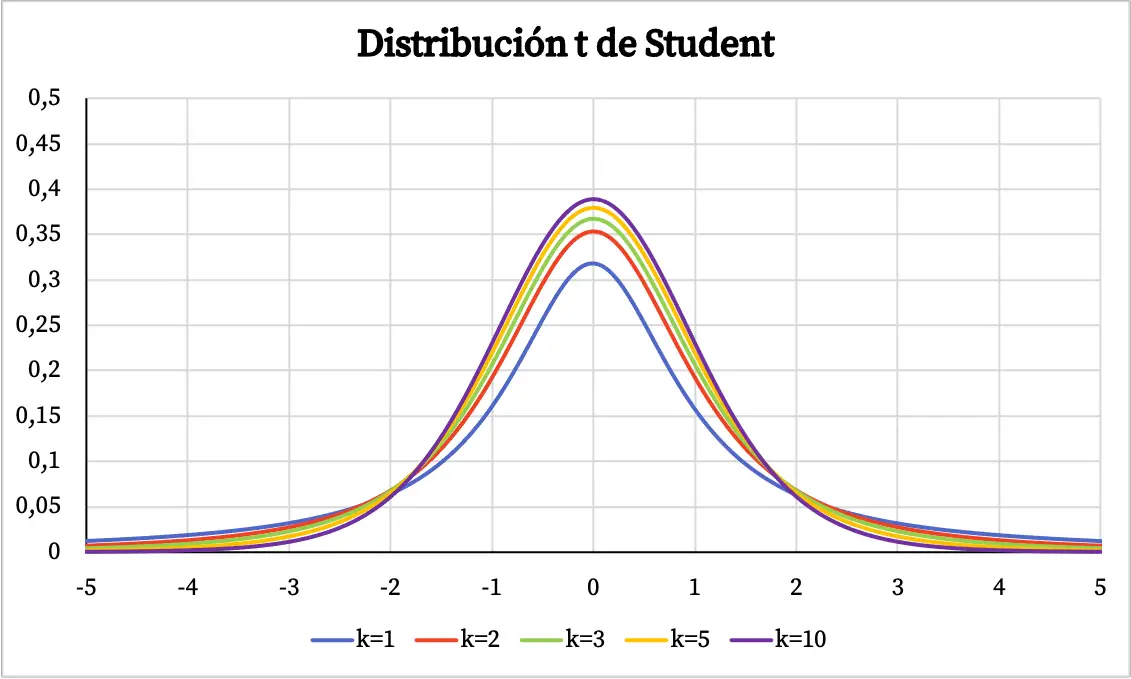
Du graphique de la distribution t de Student, les propriétés suivantes peuvent être déduites :
- La distribution Student t est symétrique centrée en 0 et a une forme de cloche.
- La distribution t de Student est plus dispersée que la distribution normale, c’est-à-dire que la courbe de la distribution t de Student est plus large.
- Plus la distribution t de Student a de degrés de liberté, plus sa dispersion est faible.
Dans le graphique ci-dessus, la fonction de densité de la distribution t de Student a été représentée en fonction de ses degrés de liberté. Cependant, vous pouvez voir ci-dessous comment la fonction de probabilité cumulée de la distribution t de Student varie :
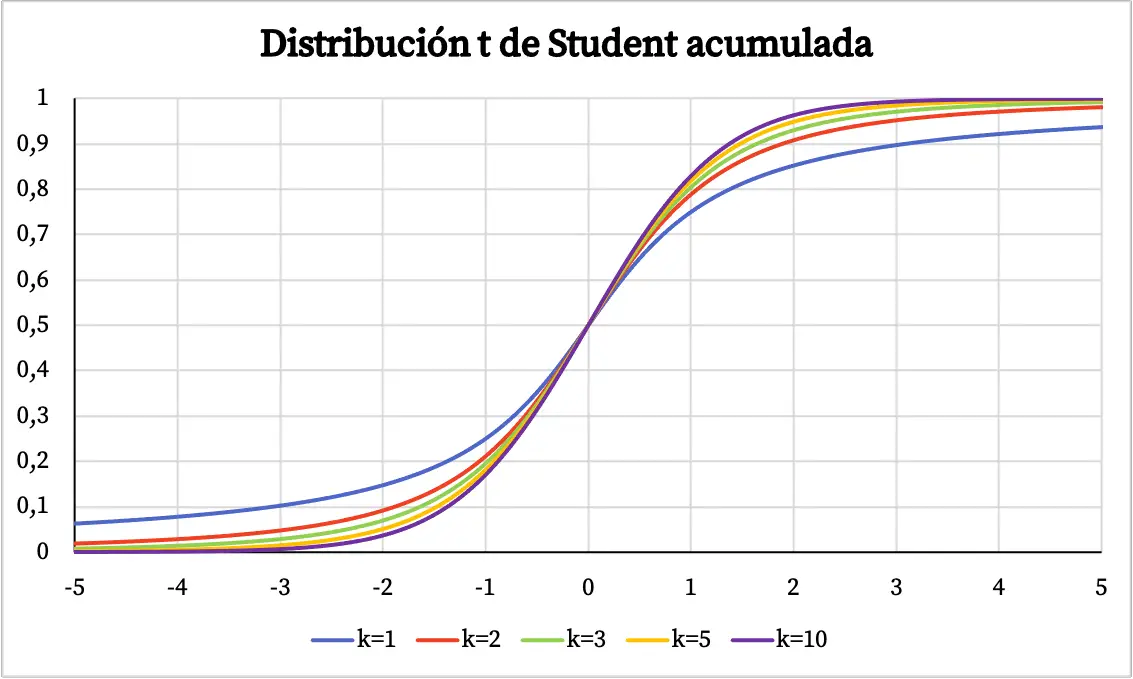
Caractéristiques de la distribution t de Student
Les caractéristiques les plus importantes de la distribution t de Student sont présentées ci-dessous.
- Le domaine de la distribution t de Student est constitué de nombres réels.
- Pour les distributions t de Student avec plus d’un degré de liberté, la moyenne de la distribution est égale à 0.
![\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d4fed5eadcaa1162752aeedb7f8a0906_l3.png "Rendered by QuickLaTeX.com")
- La variance d’une distribution t de Student peut être calculée à l’aide de l’expression suivante :
![\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-bfdcbc8a5f071a61e091b0ef6f686a16_l3.png "Rendered by QuickLaTeX.com")
- La médiane et le mode de la distribution t de Student, quel que soit le nombre de degrés de liberté, sont toujours 0.
![\begin{array}{c}Me=0\\[2ex]Mo=0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8d90790fce0c987648c0b30216c82214_l3.png "Rendered by QuickLaTeX.com")
- La fonction de densité de la distribution t de Student est définie par la formule suivante :
![\displaystyle P[X=x]=\frac{\Gamma((\nu+1)/2)} {\sqrt{\nu\pi}\,\Gamma(\nu/2)} (1+x^2/\nu)^{-(\nu+1)/2}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8c0f1e97a8e407e8b9e2b00ba93aee0e_l3.png "Rendered by QuickLaTeX.com")
- La fonction de distribution de probabilité cumulative de la distribution t de Student est définie par la formule suivante :
![\displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}](https://statorials.org/wp-content/ql-cache/quicklatex.com-da1e3bdf2d87c3a7dcc89c236958dcec_l3.png "Rendered by QuickLaTeX.com")
- Pour les distributions t de Student avec des degrés de liberté supérieurs à 3, le coefficient d’asymétrie est nul car il s’agit d’une distribution symétrique.
- Si les degrés de liberté de la distribution t de Student sont supérieurs à quatre, l’aplatissement peut être calculé en divisant six par les degrés de liberté moins quatre.
Applications de la distribution t de Student
La distribution t de Student est une distribution de probabilité largement utilisée en statistique. En fait, il existe même le test t de Student, qui sert à tester des hypothèses et des intervalles de confiance.
Ainsi, la distribution t de Student nous permet d’analyser la différence entre les moyennes de deux échantillons, plus précisément, elle est utilisée pour déterminer si deux échantillons ont des moyennes significativement différentes. De même, le test t de Student est utilisé pour savoir si la droite obtenue à partir d’une analyse de régression linéaire a une pente ou non.
En bref, les applications de la distribution t de Student reposent sur l’analyse d’ensembles de données qui suivent théoriquement une distribution normale mais que le nombre total d’observations est trop petit pour utiliser ce type de distribution.
à propos de l'auteur
Pr Amélia Rodriguez
En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus