Une introduction à la distribution triangulaire
La distribution triangulaire est une distribution de probabilité continue avec une fonction de densité de probabilité en forme de triangle.
Il est défini par trois valeurs :
- La valeur minimale a
- La valeur maximale b
- La valeur maximale c
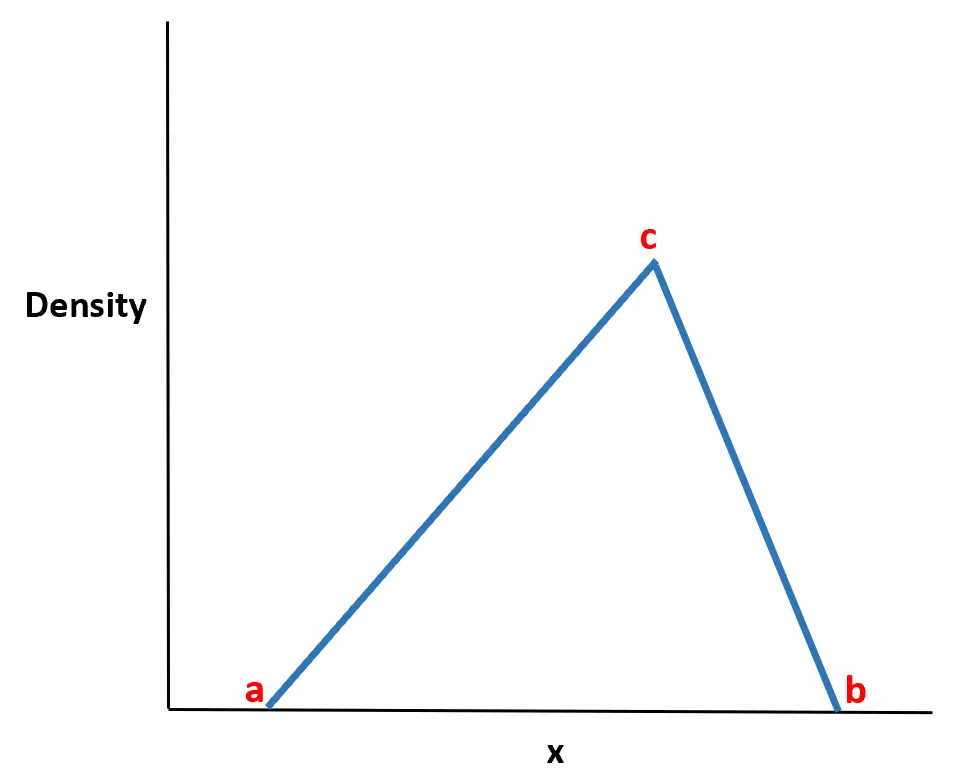
Le nom de la distribution vient du fait que la fonction de densité de probabilité a la forme d’un triangle.
Il s’avère que cette distribution est extrêmement utile dans le monde réel car nous pouvons souvent estimer la valeur minimale (a), la valeur maximale (b) et la valeur la plus probable (c) qu’une variable aléatoire prendra. peut souvent modéliser le comportement de variables aléatoires en utilisant une distribution triangulaire en connaissant uniquement ces trois valeurs.
Par exemple, un restaurant peut estimer que ses ventes totales pour la semaine à venir seront d’un minimum de 10 000 $, d’un maximum de 30 000 $ et très probablement de 25 000 $.
En utilisant uniquement ces trois nombres, ils pourraient utiliser une distribution triangulaire pour déterminer la probabilité de réaliser un certain nombre de ventes.
Propriétés de la distribution triangulaire
La distribution triangulaire a les propriétés suivantes :
PDF :
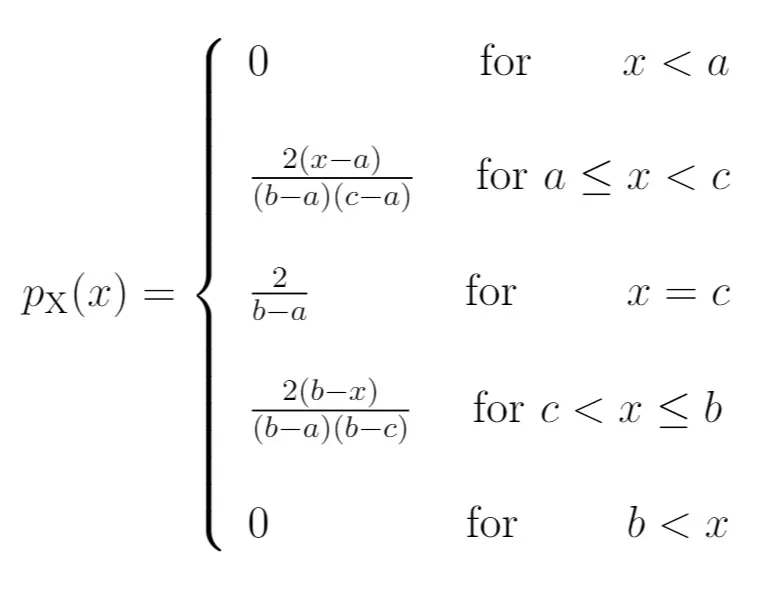
CDF :
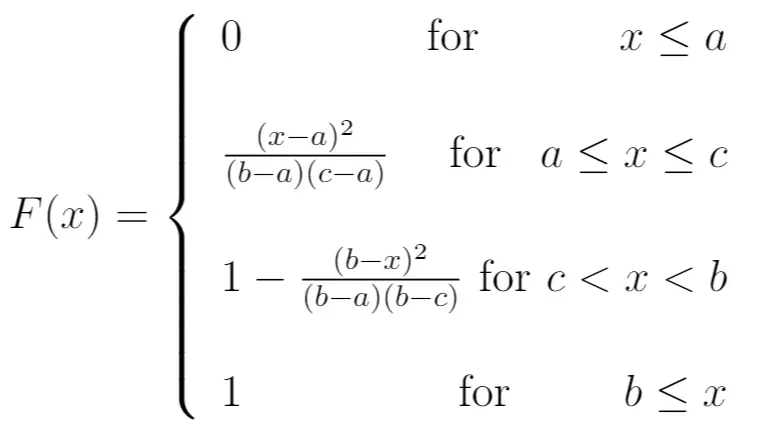
Moyenne : (a + b + c) / 3
Mode : c
Variance : (a 2 + b 2 + c 2 – ab – ac – bc) / 18
Exemple d’utilisation de la distribution triangulaire
Revenons à l’exemple précédent. Supposons qu’un restaurant estime que ses ventes totales pour la semaine à venir seront d’un minimum de 10 000 $, d’un maximum de 30 000 $ et très probablement de 25 000 $.
Quelle est la probabilité que le restaurant réalise un chiffre d’affaires total inférieur à 20 000 $ ?
Pour répondre à cette question, nous pouvons poser x = ventes totales. Nous savons que x est compris entre la valeur minimale a de 10 000 $ et la valeur maximale c de 25 000 $.
Ainsi, selon le PDF, nous pouvons utiliser l’équation suivante pour trouver la probabilité que le restaurant réalise moins de 20 000 $ de ventes totales :
- P(X < 20 000 $) = (xa) 2 / ((ba)(ca))
- P(X < 20 000 $) = (20 000-10 000) 2 / ((30 000-10 000)(25 000-10 000))
- P(X < 20 000 $) = 0,333
La probabilité que le restaurant réalise un chiffre d’affaires total inférieur à 20 000 $ est de 0,333 .
Quelle est la moyenne des ventes attendues pour le restaurant ?
Nous pouvons calculer les ventes moyennes attendues en utilisant la formule pour la moyenne donnée précédemment :
- Moyenne = (a + b + c) / 3
- Moyenne = (10 000 $ + 30 000 $ + 25 000 $) / 3
- Moyenne = 21 667 $
Les ventes moyennes attendues sont de 21 667 .
Ressources additionnelles
Les didacticiels suivants fournissent des introductions à d’autres distributions couramment utilisées :
La distribution normale
La distribution binomiale
La distribution de Poisson
La distribution géométrique
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus