Une introduction à la distribution uniforme

La distribution uniforme est une distribution de probabilité dans laquelle chaque valeur comprise entre un intervalle de a à b a la même probabilité de se produire.

Si une variable aléatoire X suit une distribution uniforme, alors la probabilité que X prenne une valeur comprise entre x ₁ et x ₂ peut être trouvée par la formule suivante :

P(x ₁ < X < x ₂ ) = (x ₂ – x ₁ ) / (b – une)

où:

• x ₁ : la valeur d’intérêt inférieure
• x ₂ : la valeur supérieure d’intérêt
• a : la valeur minimale possible
• b : la valeur maximale possible

Par exemple, supposons que le poids des dauphins soit uniformément réparti entre 100 et 150 livres.

Si nous sélectionnons un dauphin au hasard, nous pouvons utiliser la formule ci-dessus pour déterminer la probabilité que le dauphin choisi pèse entre 120 et 130 livres :

• P(120 < X < 130) = (130 – 120) / (150 – 100)
• P(120 < X < 130) = 10/50
• P(120 < X < 130) = 0,2

La probabilité que le dauphin choisi pèse entre 120 et 130 livres est de 0,2 .

Visualiser la distribution uniforme

Si nous créons un tracé de densité pour visualiser la distribution uniforme, il ressemblerait au tracé suivant :

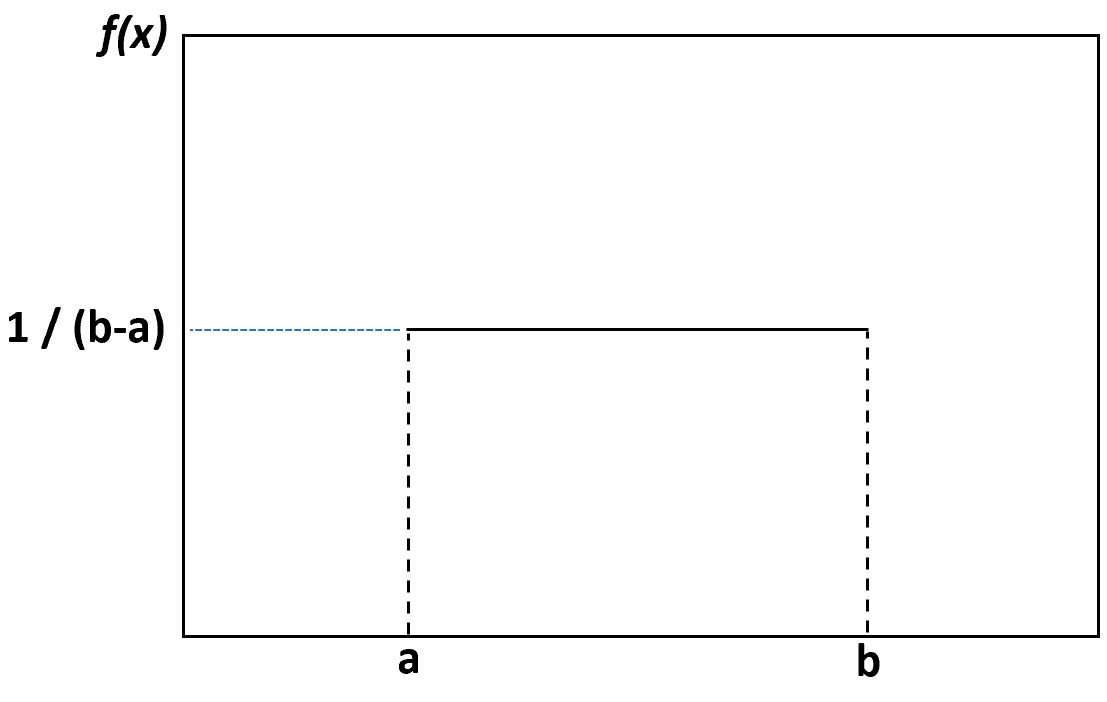
Chaque valeur comprise entre la limite inférieure a et la limite supérieure b a la même probabilité de se produire et toute valeur en dehors de ces limites a une probabilité de zéro.

Par exemple, dans notre exemple précédent, nous avons dit que le poids des dauphins est uniformément réparti entre 100 et 150 livres. Voici comment visualiser cette distribution :

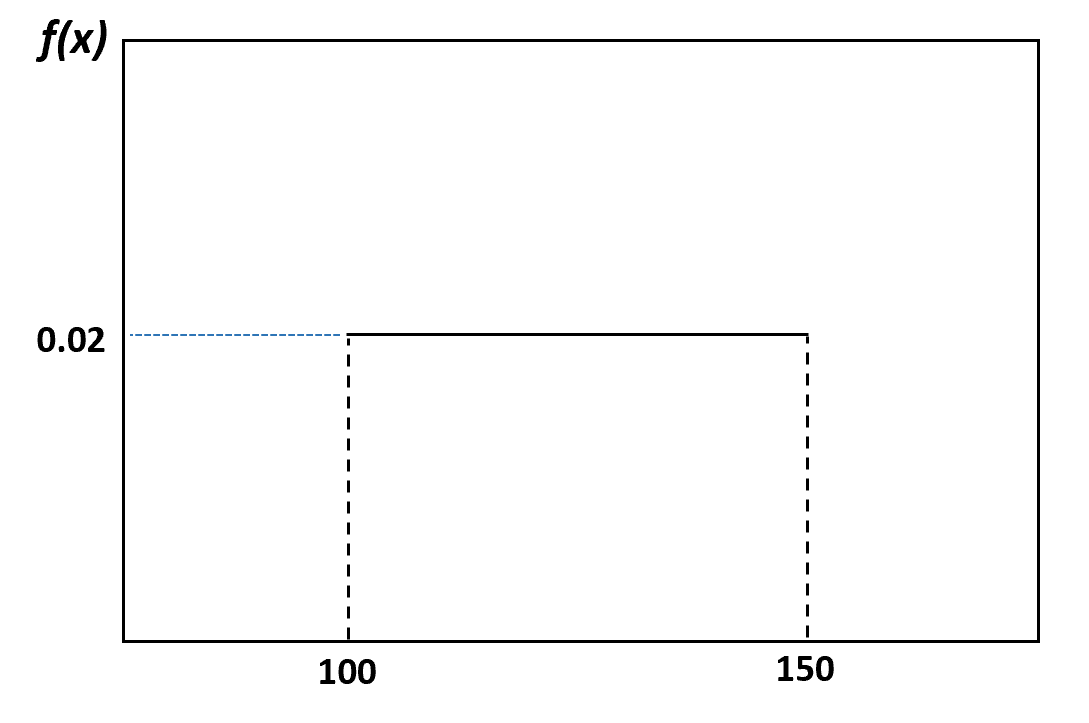
Et la probabilité qu’un dauphin sélectionné au hasard pèse entre 120 et 130 livres peut être visualisée comme suit :

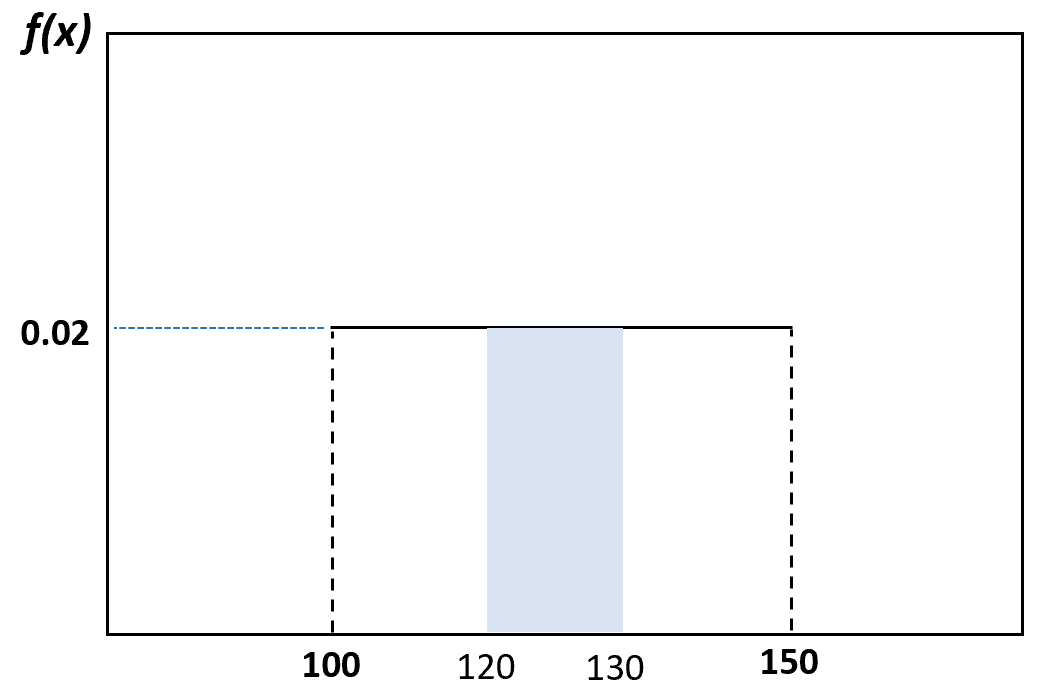
Propriétés de la distribution uniforme

La distribution uniforme a les propriétés suivantes :

• Moyenne : (a + b) / 2
• Médiane : (a + b) / 2
• Écart type : √ (b – a) ² / 12
• Écart : (b – a) ² / 12

Par exemple, supposons que le poids des dauphins soit uniformément réparti entre 100 et 150 livres.

Nous pourrions calculer les propriétés suivantes pour cette distribution :

• Poids moyen : (a + b) / 2 = (150 + 100) / 2 = 125
• Poids médian : (a + b) / 2 = (150 + 100) / 2 = 125
• Écart type de poids : √ (150 – 100) ² / 12 = 14,43
• Variation de poids : (150 – 100) ² / 12 = 208,33

Problèmes de pratiques de distribution uniforme

Utilisez les problèmes pratiques suivants pour tester vos connaissances sur la distribution uniforme.

Question 1 : Un bus se présente à un arrêt de bus toutes les 20 minutes. Si vous arrivez à l’arrêt de bus, quelle est la probabilité que le bus arrive dans 8 minutes ou moins ?

Solution 1 : la durée minimale d’attente est de 0 minute et la durée maximale est de 20 minutes. La valeur d’intérêt inférieure est de 0 minute et la valeur d’intérêt supérieure est de 8 minutes.

Ainsi, nous calculerions la probabilité comme suit :

P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0,4 .

Question 2 : La durée d’un match NBA est uniformément répartie entre 120 et 170 minutes. Quelle est la probabilité qu’un match NBA sélectionné au hasard dure plus de 155 minutes ?

Solution 2 : La durée minimale est de 120 minutes et la durée maximale est de 170 minutes. La valeur d’intérêt inférieure est de 155 minutes et la valeur d’intérêt supérieure est de 170 minutes.

Ainsi, nous calculerions la probabilité comme suit :

P(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0,3 .

Question 3 : Le poids d’une certaine espèce de grenouille est uniformément réparti entre 15 et 25 grammes. Si vous sélectionnez une grenouille au hasard, quelle est la probabilité qu’elle pèse entre 17 et 19 grammes ?

Solution 3 : Le poids minimum est de 15 grammes et le poids maximum est de 25 grammes. La valeur d’intérêt inférieure est de 17 grammes et la valeur d’intérêt supérieure est de 19 grammes.

Ainsi, nous calculerions la probabilité comme suit :

P(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0,2 .

Remarque : Nous pouvons utiliser le calculateur de distribution uniforme pour vérifier nos réponses à chacun de ces problèmes.