Qu’est-ce qu’une distribution unimodale ? (Définition & #038; Exemple)

Une distribution unimodale est une distribution de probabilité avec un pic clair.

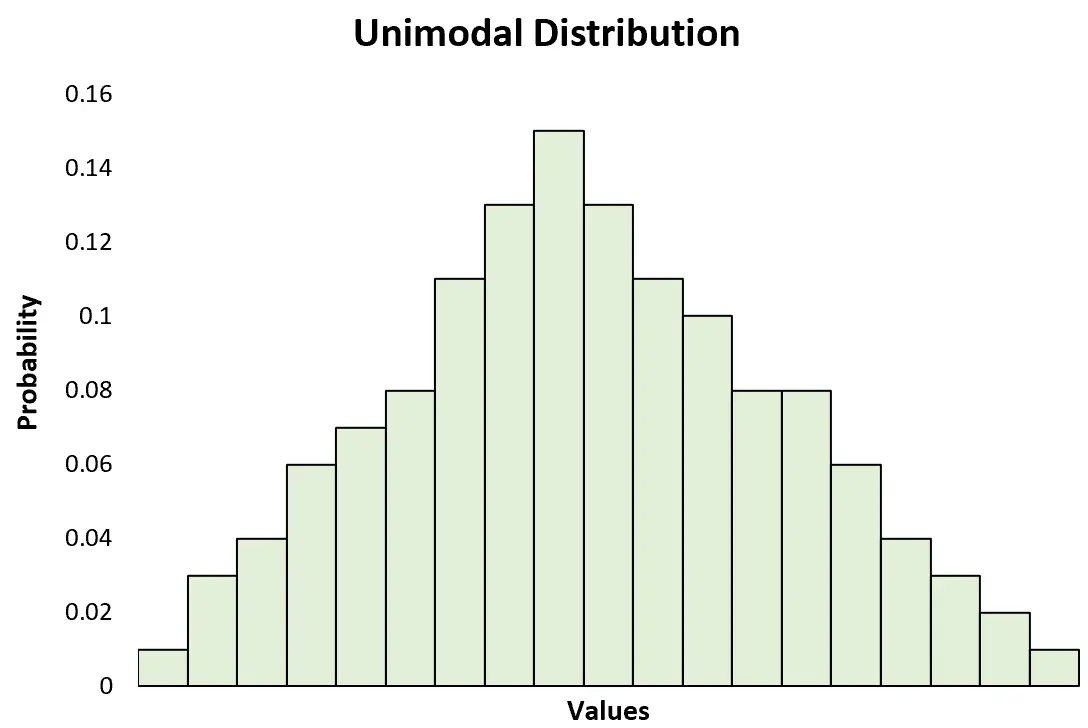
Cela contraste avec une distribution bimodale , qui présente deux pics clairs :

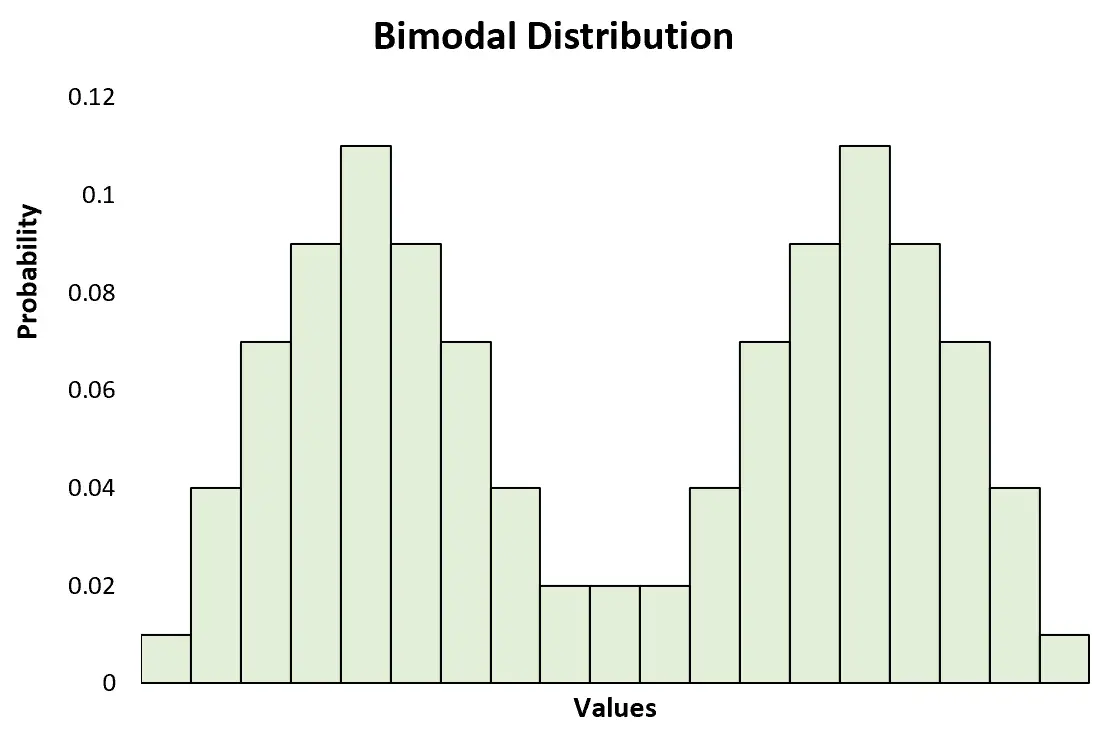
Cela contraste également avec une distribution multimodale , qui présente deux pics ou plus :

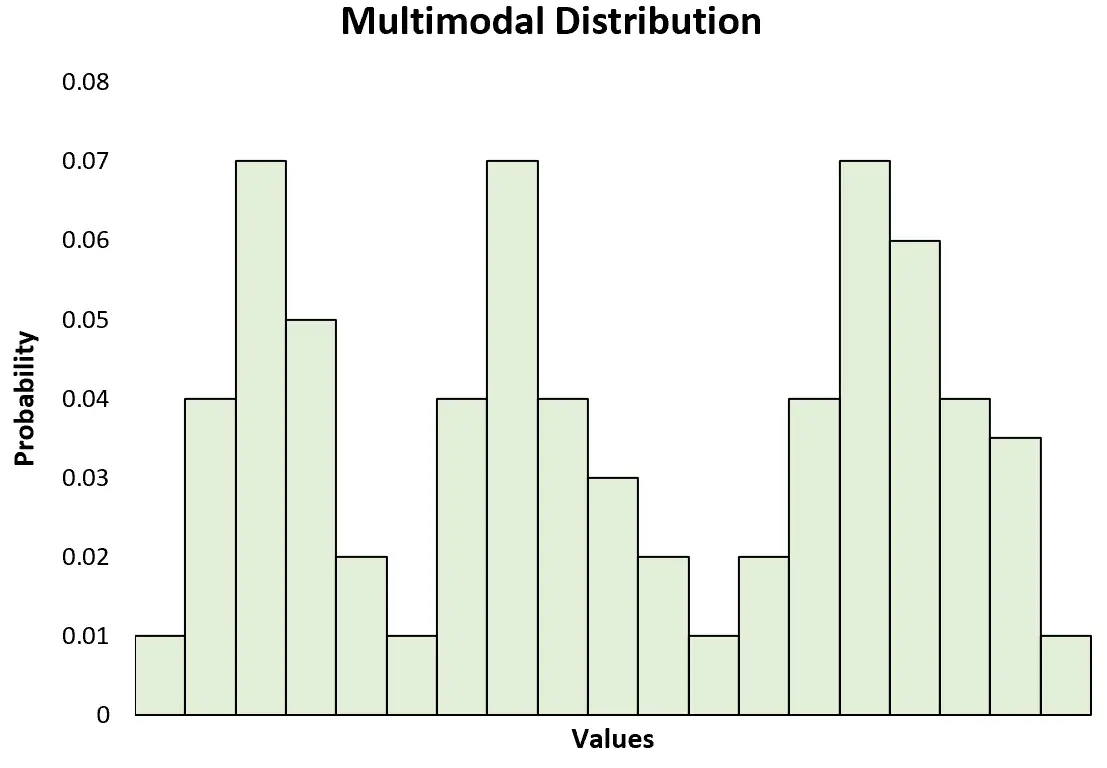
Remarque : Une distribution bimodale n’est qu’un type spécifique de distribution multimodale.

Exemples de distributions unimodales

Voici quelques exemples de distributions unimodales en pratique.

Exemple 1 : Poids à la naissance des bébés

Il est bien connu que la répartition du poids des nouveau-nés suit une répartition unimodale avec une moyenne autour de 7,5 livres. Si nous créons un histogramme du poids des bébés, nous verrons un « pic » à 7,5 livres, certains bébés pesant plus et d’autres pesant moins.

Exemple 2 : scores ACT

Le score ACT moyen des élèves du secondaire aux États-Unis est d’environ 21, certains élèves obtenant des scores inférieurs et d’autres des scores supérieurs. Si nous créons un histogramme des scores ACT pour tous les étudiants aux États-Unis, nous verrons un seul « pic » à 21 ans, avec des scores plus élevés pour certains étudiants et des scores inférieurs pour d’autres.

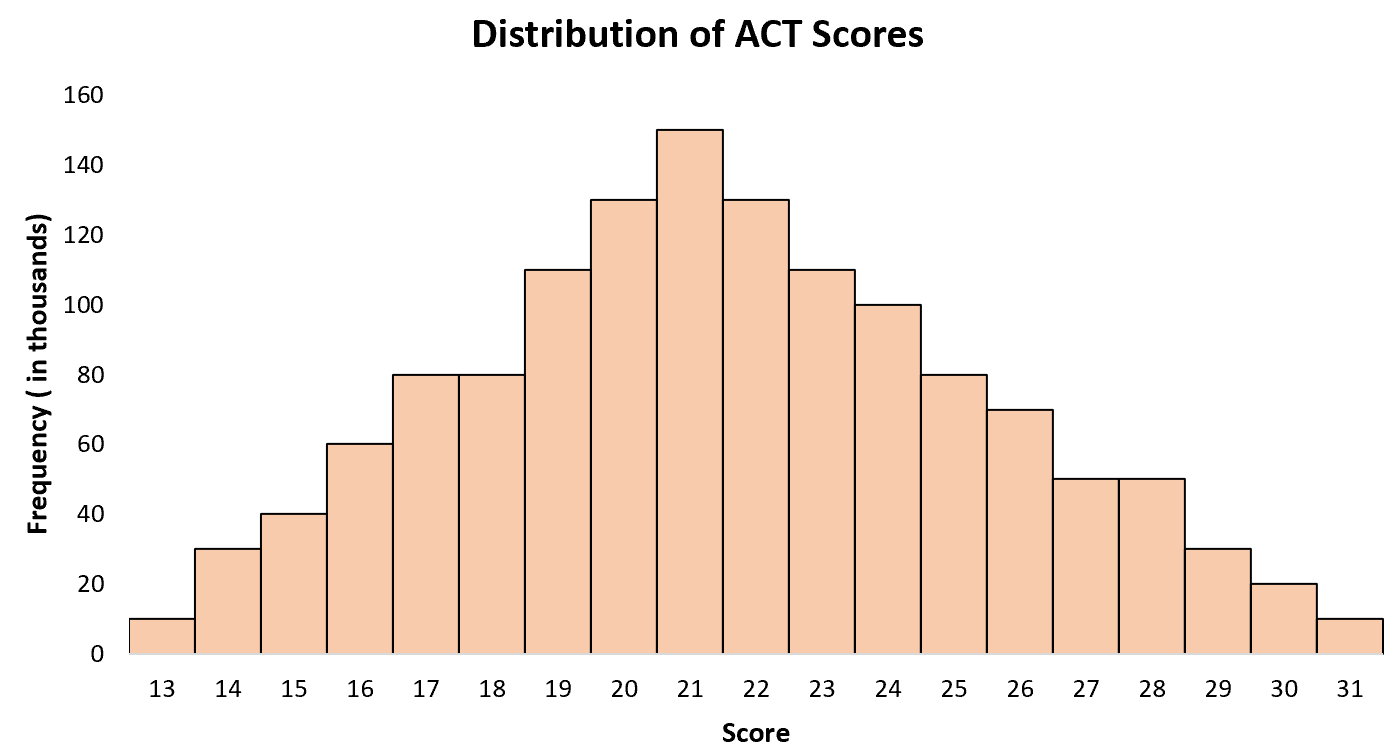
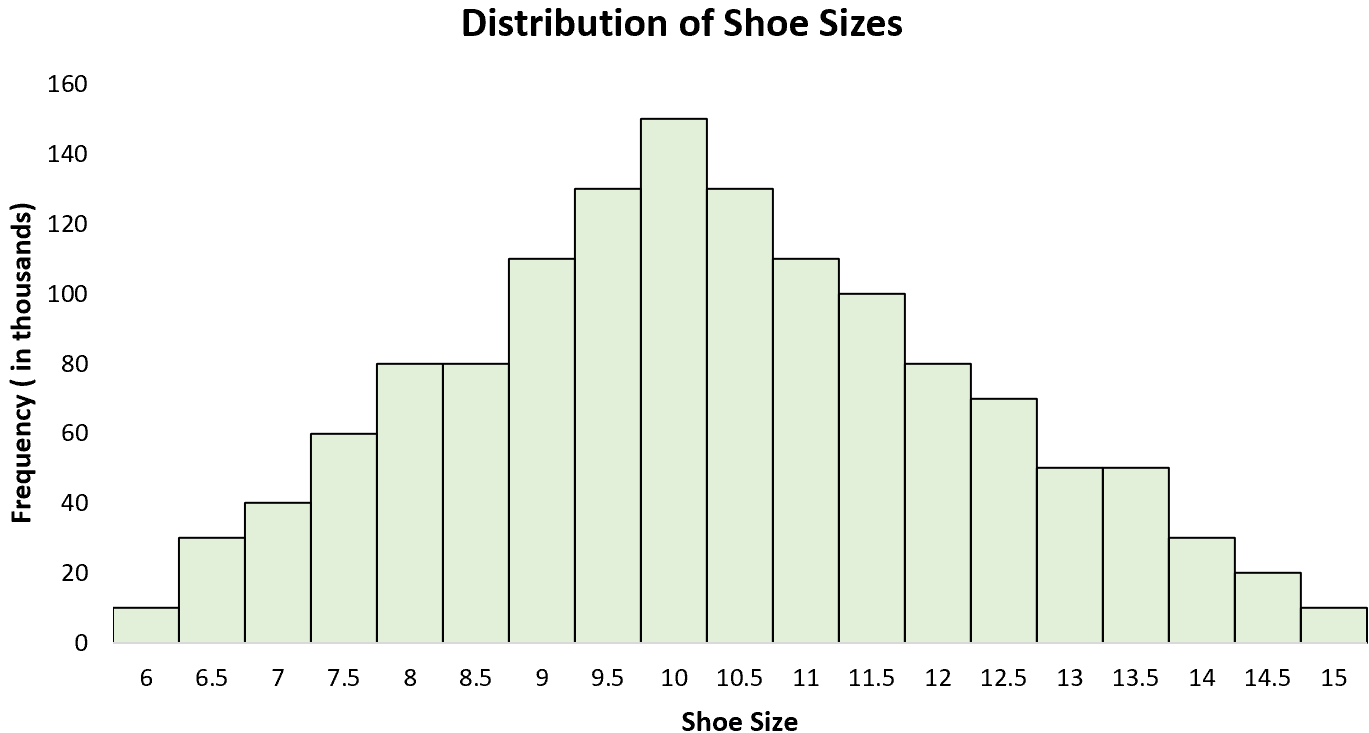
Exemple 3 : pointures de chaussures

La distribution des pointures pour hommes est une distribution unimodale avec un « pic » autour de 10. Si nous créons un histogramme de toutes les pointures pour hommes, nous verrons un seul pic à 10 avec certains hommes portant une pointure plus grande et d’autres portant une pointure plus grande. taille plus petite.

Distributions unimodales en statistiques

Les distributions de probabilité suivantes en statistiques sont toutes des distributions unimodales :

La distribution normale

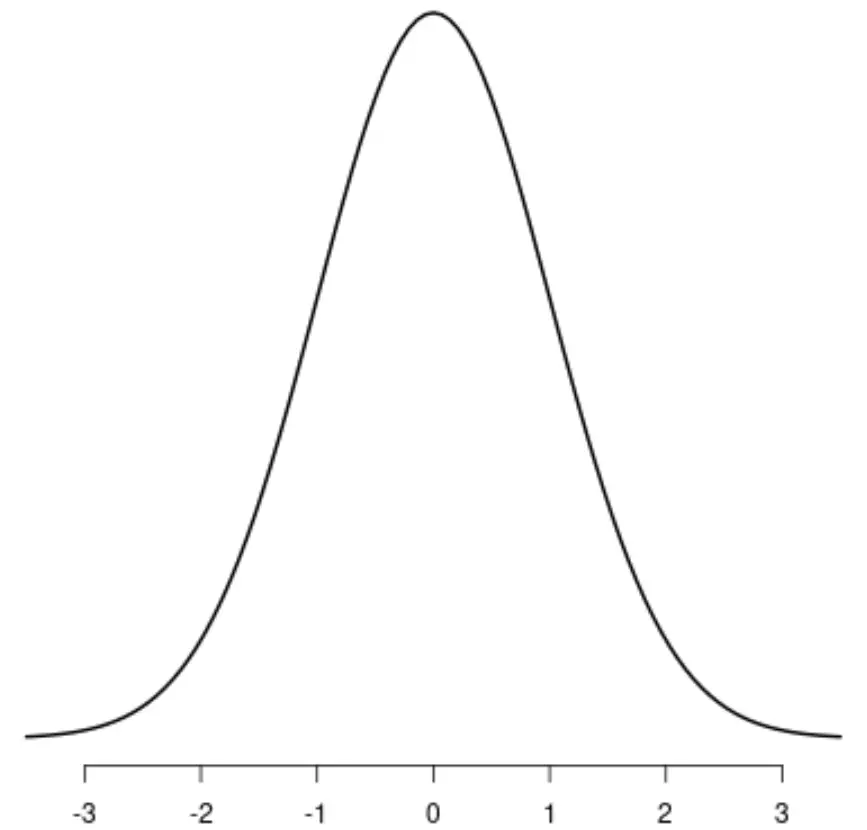
La distribution t

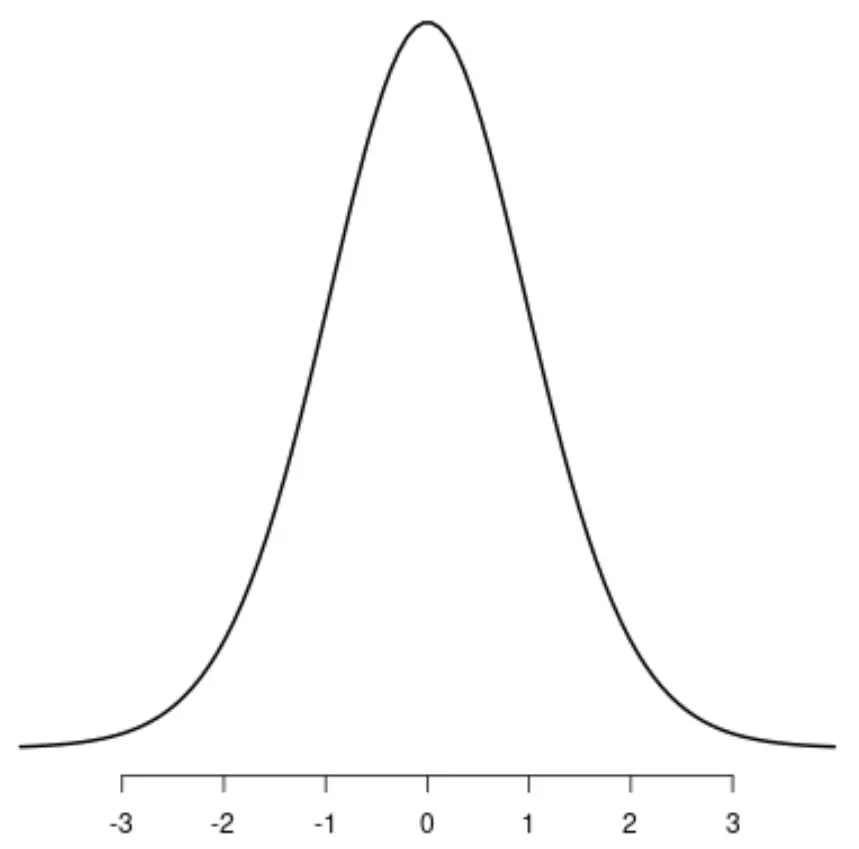
La distribution uniforme

La distribution de Cauchy

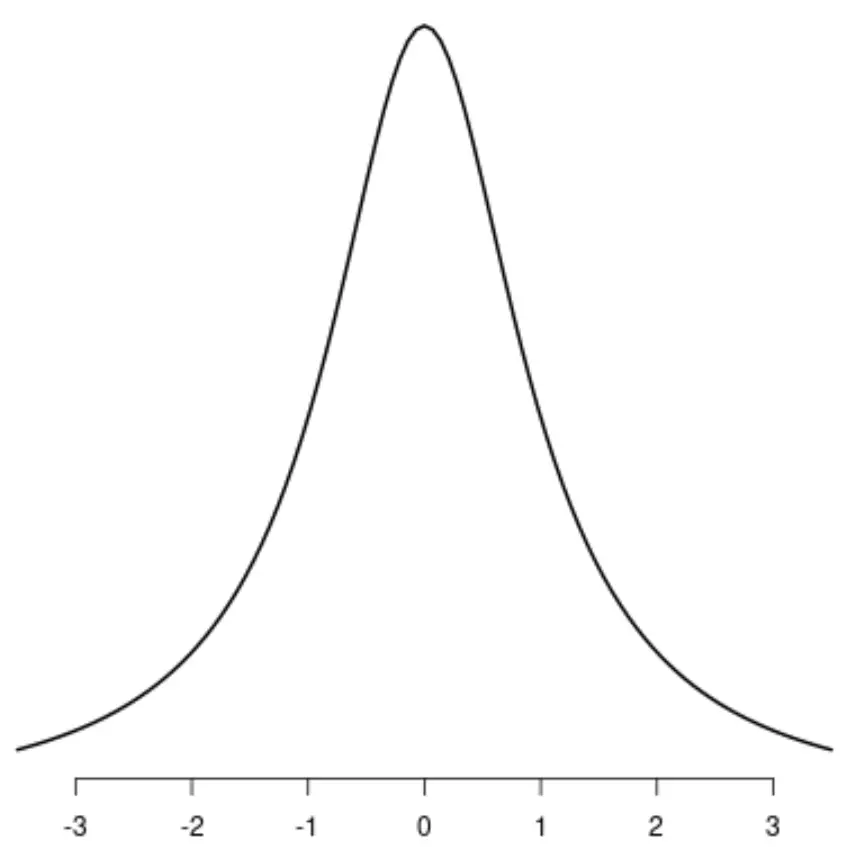
Notez que chacune de ces distributions a un seul pic distinct.

Comment analyser les distributions unimodales

Nous décrivons souvent les distributions unimodales en utilisant trois mesures différentes de tendance centrale :

• Moyenne : La valeur moyenne
• Médiane : La valeur médiane
• Mode : La valeur qui apparaît le plus souvent

En fonction de l’ asymétrie de la distribution, ces trois mesures peuvent se trouver à des endroits différents.

Distribution asymétrique à gauche : Moyenne < Médiane < Mode

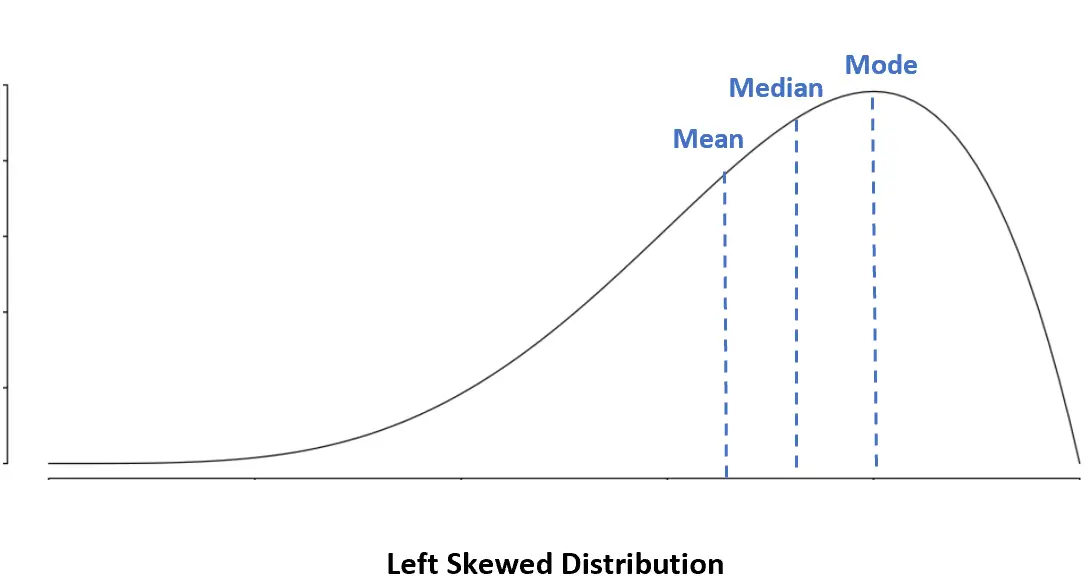
Dans une distribution asymétrique à gauche, la moyenne est inférieure à la médiane.

Distribution asymétrique à droite : Mode < Médiane < Moyenne

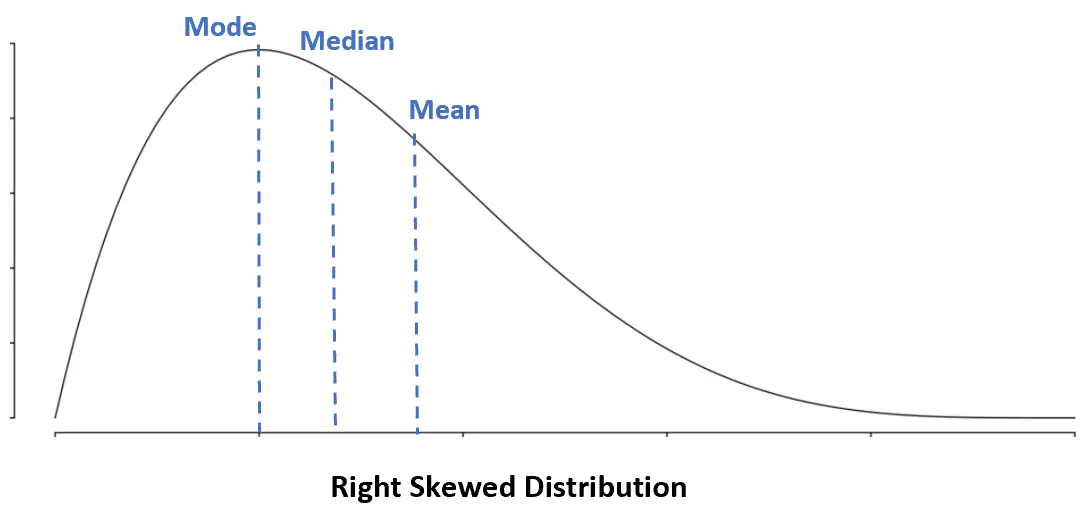
Dans une distribution asymétrique à droite, la moyenne est supérieure à la médiane.

Pas de biais : Moyenne = Médiane = Mode

Dans une distribution symétrique, la moyenne, la médiane et le mode sont tous égaux.

Ressources additionnelles

Distributions asymétriques à gauche ou à droite
Distributions symétriques : définition + exemples