Quasi-écart-type

Par Pr Amélia Rodriguez août 3, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est l’écart quasi-type dans les statistiques et comment il est calculé. Vous trouverez donc la formule de l’écart quasi-type, un exercice résolu et, en plus, un calculateur en ligne pour calculer l’écart quasi-type de n’importe quel ensemble de données.

Qu’est-ce que l’écart quasi-type ?

En statistique, l’ écart quasi-type est une mesure de dispersion qui indique la variabilité de l’échantillon. Plus précisément, l’écart quasi-type est égal à la racine carrée de la somme des carrés des écarts divisée par le nombre total de points de données moins un.

Le symbole de l’écart quasi-type est σ _n-1 os _n-1 .

L’écart quasi-type peut également être appelé quasi-écart-type , et est aussi parfois appelé écart-type d’échantillon, car il est généralement calculé à l’aide des valeurs d’un échantillon statistique. Nous entrerons ci-dessous en détail sur la différence entre l’écart quasi-type et l’écart type.

Formule d’écart quasi-type

L’écart quasi-type est égal à la racine carrée de la somme des carrés des écarts de la série de données divisée par le nombre total d’observations moins un. Par conséquent, la formule pour calculer l’écart quasi-type est la suivante :

formule de quasi-écart-type (ou quasi-écart-type)

Où:

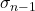$\sigma_{n-1}$ C’est le quasi-écart-type.
$x_i$ est la valeur des données $i$ .
$n$ est le nombre total de données.
$\overline{x}$ est la moyenne de l’ensemble de données.

Vous pouvez utiliser la calculatrice ci-dessous pour calculer l’écart quasi-type pour n’importe quel ensemble de données.

Exemple de calcul de l’écart quasi-type

Compte tenu de la définition de l’écart quasi-standard, vous pouvez voir ci-dessous un exemple simple de la façon de calculer l’écart quasi-standard d’un ensemble de données.

Le budget d’une entreprise pour son département de recherche et développement est très volatile, car il dépend du bénéfice économique que l’entreprise a obtenu l’année précédente. Ainsi, le budget de cette section au cours des cinq dernières années était de : 3, 6, 2, 9, 4 millions d’euros. Calculez l’écart quasi-type de cette série de données.

La première chose que nous devons faire pour déterminer l’écart quasi-type est de calculer la moyenne arithmétique de l’échantillon. Pour ce faire, nous additionnons toutes les données et divisons par le nombre total d’observations, qui est de cinq :

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Ensuite, nous appliquons la formule du quasi-écart-type :

$\displaystyle\sigma_{n-1}=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n-1}}$

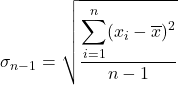
Nous substituons les données dans la formule :

$\displaystyle \sigma_{n-1}=\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5-1}}$

Et enfin on fait le calcul de l’écart quasi-type :

$\begin{aligned}\displaystyle\sigma_{n-1} & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5-1}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{4}}\\[2ex]&= \sqrt{\frac{30,8}{4}}=\sqrt{7,7}=2,77 \end{aligned}$

En bref, le quasi-écart-type de l’échantillon de données est de 2,77 millions d’euros.

➤ Voir : Quasivariance

Calculateur d’écart quasi-type

Branchez un ensemble de données statistiques dans le calculateur en ligne ci-dessous pour calculer son écart quasi-type. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Écart quasi-standard et écart-type

Enfin, nous verrons quelle est la différence entre l’écart quasi-type et l’écart type, puisqu’il s’agit de deux mesures statistiques différentes qui portent un nom très similaire et sont calculées de manière très similaire.

La différence entre l’écart quasi-type et l’écart type est le dénominateur de la formule. Pour calculer l’écart quasi-type, divisez par n-1, mais l’écart type est calculé en divisant par n.

Par conséquent, l’écart quasi-type et l’écart type sont mathématiquement liés, puisque l’écart quasi-type équivaut à l’écart type multiplié par la racine carrée de n (nombre total de points de données) sur n-1.

$\displaystyle\sigma_{n-1}=\sqrt{\frac{n}{n-1}}\cdot \sigma$

De l’équation précédente on peut déduire que, pour un même ensemble de données, la valeur du quasi-écart-type sera toujours supérieure à la valeur de l’écart-type.

De plus, la formule de l’écart quasi-type est souvent utilisée pour calculer l’écart type d’un échantillon car elle élimine les biais. Le quasi-écart-type est donc un bon estimateur de l’écart-type de la population. C’est pourquoi, lorsqu’on fait une inférence statistique à partir d’un échantillon, il est assez courant de dire que l’écart type est calculé alors qu’en réalité, c’est l’écart quasi-type qui est calculé.

➤ Voir : Propriétés de l’écart type

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus