Échantillon statistique

Cet article explique ce qu’est un échantillon statistique et à quoi il sert. Vous pourrez également voir la différence entre les notions de population et d’échantillon ainsi que plusieurs exemples d’échantillons statistiques. De plus, il montre les caractéristiques qu’un échantillon doit posséder pour être représentatif.

Qu’est-ce qu’un échantillon statistique ?

Un échantillon statistique est un groupe d’individus issus d’une population statistique. Autrement dit, en statistique, un échantillon est la partie de la population sur laquelle l’étude statistique est réalisée.

Par exemple, lorsqu’un sondage électoral est réalisé, l’échantillon statistique est constitué de l’ensemble des personnes interrogées.

Normalement, lorsqu’on veut faire une recherche, on ne peut pas étudier tous les éléments qui composent le groupe d’étude. À l’instar de l’exemple précédent, il est impossible d’examiner toutes les personnes qui votent à une élection. Par conséquent, un échantillon est généralement choisi pour analyser seulement une partie du groupe d’étude, puis extrapoler les résultats à l’ensemble du groupe.

Cela peut être réalisé grâce à l’inférence statistique, car elle permet de déterminer les paramètres de la population à partir des résultats de l’échantillon avec une très petite marge d’erreur.

Échantillon et population

En statistique, une population est un ensemble d’éléments présentant des caractéristiques similaires sur lesquels une étude statistique est destinée à être réalisée. On peut faire référence à ce concept avec le terme population statistique ou simplement avec population.

La différence entre un échantillon statistique et une population statistique est la proportion par rapport au nombre total d’éléments de l’étude, puisque l’échantillon fait partie de la population, qui représente tous les éléments qui composent le groupe destiné à être analysé.

La taille d’un échantillon sera donc toujours inférieure ou égale à la taille d’une population.

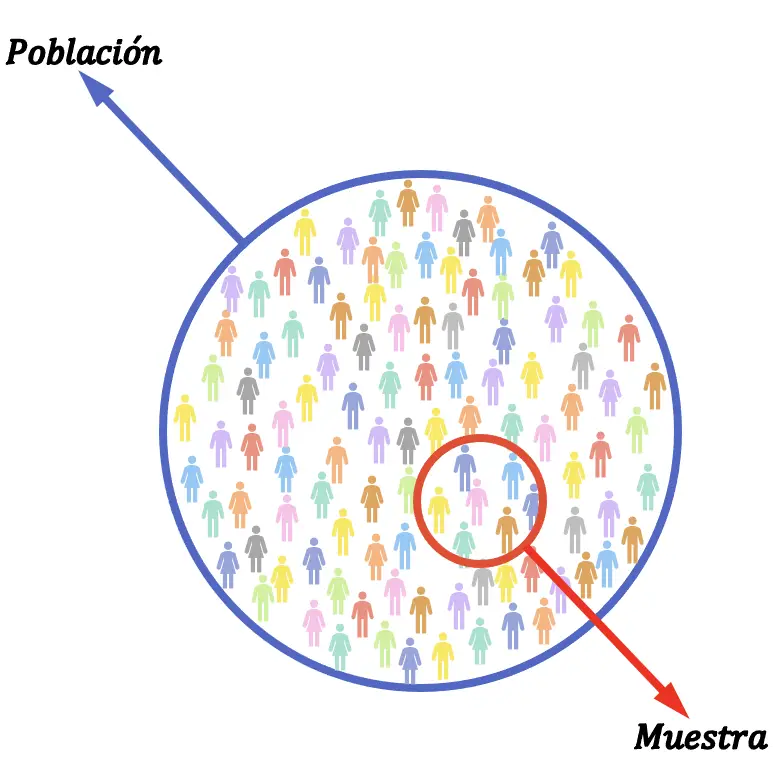
Par exemple, si nous voulons faire une étude statistique sur la proportion de pièces défectueuses produites par une usine, nous n’étudierons pas toutes les pièces fabriquées, mais plutôt seulement un ensemble de pièces sélectionnées au hasard. Ainsi, dans ce cas, la population est constituée des pièces produites par l’usine et, d’autre part, l’échantillon est l’ensemble des pièces analysées dans l’étude statistique.

Il est important que l’échantillon choisi pour réaliser l’enquête statistique soit représentatif des caractéristiques de la population, afin que les conclusions tirées de l’échantillon puissent être extrapolées à l’ensemble de la population. Nous verrons ensuite comment sélectionner des individus à partir d’un échantillon.

Échantillon et échantillonnage

En statistique, l’échantillonnage est un processus par lequel un échantillon est sélectionné parmi une population. Autrement dit, l’échantillonnage est une méthode par laquelle un groupe d’individus est sélectionné pour réaliser une étude statistique.

Par exemple, une façon de procéder à un échantillonnage consiste à sélectionner des individus au hasard. Ainsi, si nous voulons étudier la taille d’une population statistique, nous pouvons sélectionner l’échantillon d’étude par simple échantillonnage aléatoire.

Il existe plusieurs méthodes pour échantillonner une population, chacune ayant ses avantages et ses inconvénients. Cliquez sur le lien suivant pour voir quels sont les différents types d’échantillonnage statistique.

Taille de l’échantillon

La taille de l’échantillon (ou taille de l’échantillon ) est le nombre d’individus qui composent l’échantillon d’une étude. En statistique, la taille de l’échantillon est importante afin que l’échantillon soit représentatif de l’ensemble de la population.

Par exemple, si l’on veut faire une analyse sur la hauteur d’un pays, on ne peut pas demander la taille de tous les habitants du pays, car l’enquête prendrait beaucoup de temps et serait trop coûteuse. Il faut donc procéder à un échantillonnage aléatoire et interroger uniquement un échantillon représentatif de la population.

Cependant, la taille de l’échantillon d’une étude statistique doit être suffisamment grande pour représenter les caractéristiques de l’ensemble de la population. En revanche, la taille de l’échantillon ne peut pas être excessivement grande, car la recherche devient alors plus coûteuse. La taille de l’échantillon doit donc être appropriée, ni trop grande ni trop petite. Vous pouvez voir comment calculer la taille d’échantillon appropriée ici :

Échantillon représentatif

En statistiques, un échantillon représentatif est un échantillon qui représente de manière adéquate les individus d’une population. Autrement dit, un échantillon représentatif est une partie d’une population dont les caractéristiques sont similaires à celles de la population qu’il représente.

Il est important que l’échantillon d’une enquête statistique soit représentatif afin que les résultats obtenus puissent être appliqués à l’ensemble de la population. Si l’échantillon étudié n’est pas représentatif, on obtiendra des résultats qui ne coïncideront pas avec la population et, par conséquent, des conclusions erronées seront tirées.

La méthode pour obtenir un échantillon représentatif ne peut pas reposer sur la sélection d’un groupe d’individus au hasard, mais la représentativité d’un échantillon dépend de plusieurs facteurs tels que la méthode d’échantillonnage, la taille de l’échantillon, la marge d’erreur, le niveau de confiance, etc.

Premièrement, la technique d’échantillonnage appropriée doit être utilisée pour obtenir un échantillon représentatif. Il existe plusieurs types d’échantillonnage et chacun est adapté à un type d’échantillon, de sorte qu’en fonction des caractéristiques de la population, il est préférable d’utiliser une technique d’échantillonnage ou une autre.

Dans le lien suivant, vous pouvez voir quels sont les différents types d’échantillonnage et quel type d’échantillonnage est idéal pour chaque situation :

De plus, vous devez éviter de commettre des erreurs d’échantillonnage. Une erreur d’échantillonnage est une erreur commise lors du processus d’obtention d’un échantillon et qui fait que les caractéristiques de l’échantillon sont différentes de celles de la population. Par conséquent, l’estimation des paramètres de la population à travers les données de l’échantillon est incorrecte. Il faut donc prêter attention à la fois au processus d’échantillonnage et à la méthode d’échantillonnage choisie.

Deuxièmement, un échantillon représentatif doit être de taille adéquate. Pour qu’un échantillon représente les propriétés d’une population, le nombre d’observations dans l’échantillon doit être suffisamment grand. En revanche, la taille de l’échantillon ne peut pas être trop grande car le prix de la recherche est trop élevé. En bref, il faut trouver un équilibre entre représentativité et coût de l’échantillon pour choisir la taille idéale de l’échantillon.

Avantages d’un échantillon en statistiques

Enfin, voyons quels sont les avantages d’étudier un échantillon plutôt que l’ensemble de la population en résumé :

• L’examen d’un échantillon seulement rend l’étude statistique plus facile, car moins d’individus doivent être étudiés.
• Le coût économique de l’étude est réduit, puisque les dépenses pour collecter les données sont moindres.
• Cela permet de mener l’enquête plus rapidement car moins de données doivent être collectées.
• Il permet de réaliser des études statistiques qui seraient impossibles à réaliser s’il fallait analyser tous les individus de la population.