Échantillonnage aléatoire simple

Par Pr Amélia Rodriguez août 6, 2023 Statistiques 0 commentaire

Dans cet article, vous découvrirez ce qu’est un échantillon aléatoire simple et quels types d’échantillons aléatoires simples il existe. De plus, nous expliquons comment un échantillonnage aléatoire simple est réalisé à travers un exemple. Enfin, vous pourrez voir quels sont les avantages et les inconvénients de l’échantillonnage aléatoire simple.

Qu’est-ce que l’échantillonnage aléatoire simple ?

En statistiques, l’échantillonnage aléatoire simple est une méthode probabiliste utilisée pour sélectionner l’échantillon pour une étude. La principale caractéristique de l’échantillonnage aléatoire simple est qu’il donne à chaque élément de la population statistique la même probabilité d’être inclus dans l’échantillon étudié.

Dans un échantillonnage aléatoire simple, les éléments de l’échantillon sont choisis au hasard, de sorte que l’échantillon obtenu est totalement aléatoire.

Par conséquent, en utilisant un échantillonnage aléatoire simple, la probabilité d’obtenir un échantillon donné est égale aux probabilités d’obtenir tout autre échantillon. Nous verrons ci-dessous comment cette probabilité est calculée.

Gardez à l’esprit qu’il existe d’autres façons de sélectionner les individus dans un échantillon. Les types d’échantillonnage les plus utilisés sont principalement :

Échantillonnage aléatoire simple
Échantillonnage stratifié
Échantillonnage systématique
Échantillonnage en grappes

Le concept d’échantillonnage aléatoire simple est certainement le type le plus facile à comprendre, mais il s’avère parfois le plus compliqué à mettre en œuvre, précisément en raison de son caractère aléatoire.

Comment faire un échantillonnage aléatoire simple

Les étapes pour effectuer un échantillonnage aléatoire simple sont les suivantes :

Faites une liste avec tous les éléments de la population.
Attribuez un numéro séquentiel (1, 2, 3,…, n) à chaque élément de la population.
Définissez la taille d’échantillon souhaitée.
Utilisez un générateur de nombres aléatoires pour générer autant de nombres que la taille de l’échantillon choisie.
Les individus affectés aux numéros générés sont ceux sélectionnés pour faire partie de l’échantillon.

Pour générer des nombres aléatoires, il existe plusieurs méthodes, les plus traditionnelles sont la méthode de la loterie et la méthode des tables de nombres :

La méthode de loterie consiste à mettre tous les numéros dans une case, à les mélanger puis à tirer des numéros au hasard.
La méthode du tableau de nombres consiste à sélectionner des nombres au hasard dans un tableau contenant tous les nombres possibles.

Bien que vous puissiez également utiliser l’une ou l’autre des deux méthodes précédentes, celles-ci nécessitent plus de temps et conviennent mieux aux échantillons de petite taille. Actuellement, des programmes informatiques sont utilisés pour générer des nombres aléatoires plus rapidement, par exemple vous pouvez utiliser le programme Excel.

D’autre part, vous devez tenir compte du fait que la taille de l’échantillon doit être adéquate, afin d’avoir le minimum d’erreur d’échantillonnage possible. Trouver la taille d’échantillon idéale n’est pas anodin ; si vous avez des doutes à ce sujet, vous pouvez rechercher sur notre site Web l’article dans lequel nous expliquons comment procéder.

Exemple d’échantillonnage aléatoire simple

Une fois que nous aurons vu la définition de l’échantillonnage aléatoire simple, nous allons voir un exemple résolu de la façon dont ce type d’échantillonnage est effectué.

Par exemple, s’il y a 2000 travailleurs dans une entreprise et que nous voulons réaliser une étude statistique avec un échantillon de 400 travailleurs, pour sélectionner les individus qui feront partie de l’échantillon avec un échantillonnage aléatoire simple, la première chose à faire consiste à attribuer à chaque employé un numéro de 1 à 2000.

Après l’attribution des numéros, nous devons sélectionner au hasard 400 numéros. Dans ce cas, la taille de l’échantillon est assez grande, il est donc préférable d’utiliser un logiciel informatique tel qu’Excel.

Ensuite, les 400 travailleurs sélectionnés pour participer à l’étude seront ceux dont le numéro attribué a été déterminé à l’étape précédente.

Dans cet exemple, on a considéré que 400 éléments constituaient une taille d’échantillon suffisamment représentative, mais logiquement ce nombre changera en fonction de l’expérience.

Types d’échantillonnage aléatoire simple

Il existe deux types d’échantillonnage aléatoire simple :

Échantillonnage aléatoire simple avec remise : l’élément sélectionné de la base de sondage est renvoyé et peut être à nouveau sélectionné.
Échantillonnage aléatoire simple sans remplacement : L’élément sélectionné pour faire partie de l’échantillon est supprimé et ne peut plus être sélectionné.

L’échantillonnage aléatoire simple avec remise est le type d’échantillonnage le plus simple, puisque exactement le même processus est toujours répété pour sélectionner un élément de l’échantillon. Cependant, l’échantillonnage aléatoire simple sans remise est plus largement utilisé car plus précis. Les deux types sont expliqués plus en détail ci-dessous.

Échantillonnage aléatoire simple avec remise

L’échantillonnage aléatoire simple avec remise consiste à renvoyer chaque élément sélectionné dans la base d’échantillonnage pour que la possibilité de le choisir à nouveau existe.

Par conséquent, il est possible d’obtenir un échantillon avec un seul élément sélectionné plusieurs fois, bien que cela soit évidemment très improbable.

Mathématiquement, il s’agit d’un type d’échantillonnage très simple puisque les probabilités de chaque extraction sont les mêmes. C’est pourquoi il est habituel de commencer à étudier cette technique d’échantillonnage avant les autres.

Dans l’échantillonnage aléatoire simple avec remise, la probabilité d’obtenir un échantillon avec un certain ordre peut être calculée à l’aide de la formule suivante :

$P=\cfrac{1}{N^n}$

Être

$N$ le nombre total d’éléments de la population et $n$ le nombre d’extractions indépendantes qui seront effectuées.

En revanche, lorsque l’ordre n’a pas d’importance, la probabilité d’obtenir un échantillon est calculée à l’aide de l’expression suivante :

$P=\cfrac{n!}{\displaystyle N^n\prod_{i=1}^z k_i!}$

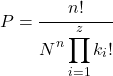
Où

$n$ est le nombre d’extractions indépendantes, $z$ le nombre d’éléments différents dans l’échantillon et $k_i$ combien de fois vous souhaitez que l’élément apparaisse $i$ dans l’échantillon.

Enfin, pour trouver la probabilité d’inclusion de l’élément

$i$ , c’est-à-dire la probabilité d’inclure l’élément $i$ Dans l’exemple, la formule suivante doit être utilisée :

$\displaystyle \pi_i=1-\left(1-\frac{1}{N}\right)^n$

Échantillonnage aléatoire simple sans remplacement

L’échantillonnage aléatoire simple sans remise consiste à sélectionner dans un échantillon autant d’individus qu’indique la taille d’échantillon souhaitée afin que chaque individu ne puisse pas être choisi à nouveau une fois sélectionné. Par conséquent, chaque élément sélectionné est supprimé et non remplacé.

Lorsqu’on parle d’échantillonnage aléatoire simple, on fait normalement référence à celui dans lequel les individus ne sont pas remplacés puisque c’est celui qui est le plus utilisé en pratique.

Pour déterminer la probabilité d’obtenir un échantillon avec un certain ordre en échantillonnage aléatoire simple avec remise, la formule suivante est utilisée :

$P=\cfrac{1}{n!\begin{pmatrix}N\\n\end{pmatrix}}$

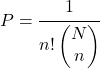
Être

$N$ le nombre total d’éléments dans la population et $n$ le nombre d’extractions dépendantes à effectuer.

En revanche, si l’ordre d’extraction ne doit pas être pris en compte, la probabilité d’obtenir un échantillon est égale à :

$P=\cfrac{1}{\begin{pmatrix}N\\n\end{pmatrix}}$

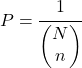
Enfin, la probabilité d’inclusion d’un élément dans un échantillonnage aléatoire simple sans remise est calculée en appliquant la règle de Laplace :

$\displaystyle \pi_i=\frac{n}{N}$

Avantages et inconvénients de l’échantillonnage aléatoire simple

L’échantillonnage aléatoire simple présente les avantages et les inconvénients suivants :

avantage	Désavantages
Facile à comprendre.	Une liste de tous les éléments de la population est nécessaire.
Tous les échantillons possibles sont équiprobables.	Cela peut être très coûteux avec des échantillons de grande taille.
Des échantillons représentatifs sont généralement obtenus.	Il a tendance à comporter des erreurs d’échantillonnage plus importantes.
Aucune connaissance technique n’est nécessaire pour effectuer l’échantillonnage.	Les connaissances que le chercheur pourrait avoir du domaine étudié ne sont pas exploitées.
Vous permet de calculer rapidement les moyennes et les écarts.	L’échantillon peut ne pas être représentatif s’il est trop petit.
Il existe des logiciels statistiques pour analyser les données.	Ne convient pas aux études nécessitant des entretiens individuels.

Comme nous l’avons vu, l’une des principales caractéristiques de l’échantillonnage aléatoire simple est qu’il est facile à comprendre et à expliquer. En effet, la personne qui réalise l’échantillonnage n’a pas besoin d’être un expert dans le domaine de l’analyse. Cependant, c’est à la fois une force et une faiblesse, car dans d’autres types d’échantillonnage, les connaissances de l’analyste peuvent être mises à profit pour obtenir un meilleur échantillonnage.

De même, l’échantillonnage étant aléatoire, les probabilités de prendre tel ou tel élément pour constituer l’échantillon étudié sont équiprobables, contrairement aux autres types d’échantillonnage.

Bien que des échantillons représentatifs de la population soient généralement obtenus, l’erreur d’échantillonnage dans l’échantillonnage aléatoire simple est importante par rapport aux autres types d’échantillonnage. De plus, l’échantillon peut même ne pas être représentatif si la taille des individus est petite.

Une propriété très intéressante de l’échantillonnage aléatoire simple est qu’il peut être réalisé à l’aide de programmes informatiques, ce qui permet d’effectuer des calculs statistiques rapidement.

Enfin, il convient de noter que l’échantillonnage aléatoire simple peut être plus coûteux que d’autres types d’échantillonnage, en particulier dans les populations très dispersées, car il peut nécessiter l’utilisation de plus de ressources pour la recherche. Par exemple, puisqu’il s’agit d’un échantillonnage aléatoire, les personnes sélectionnées pour réaliser l’étude peuvent être géographiquement très dispersées et, par conséquent, mener des entretiens en face à face coûterait beaucoup plus cher.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus