Distribution d’échantillonnage de la différence de moyennes

Par Pr Amélia Rodriguez août 3, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est la distribution d’échantillonnage de la différence entre deux moyennes dans les statistiques. Vous trouverez également la formule de répartition d’échantillonnage de la différence de moyennes et, en complément, un exercice résolu étape par étape.

Quelle est la distribution d’échantillonnage de la différence des moyennes ?

La distribution d’échantillonnage de la différence de moyennes est la distribution qui résulte du calcul des différences entre les moyennes de tous les échantillons possibles de deux populations différentes.

Autrement dit, pour obtenir la distribution d’échantillonnage de la différence de moyenne, tous les échantillons possibles de deux populations étudiées doivent être sélectionnés, puis la moyenne de chaque échantillon sélectionné est calculée et, enfin, la différence entre toutes les moyennes calculées à partir des deux populations. Ainsi, l’ensemble des valeurs obtenues après application de toutes ces opérations forme la distribution d’échantillonnage de la différence de moyennes.

La distribution d’échantillonnage de la différence des moyennes est utilisée pour calculer la probabilité que la différence entre deux moyennes d’échantillons sélectionnés au hasard provenant de deux populations différentes soit proche de la différence des moyennes des populations.

➤ Voir : Distribution d’échantillonnage de la moyenne

Formule pour la distribution d’échantillonnage de la différence de moyennes

Si la taille de l’échantillon est suffisamment grande (n ₁ ≥30 et n ₂ ≥30), la distribution d’échantillonnage de la différence de moyenne suit une distribution normale. Plus précisément, les paramètres de ladite distribution sont calculés comme suit :

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Remarque : Si les deux populations sont des distributions normales , alors la distribution d’échantillonnage de la différence de moyenne suit une distribution normale quelle que soit la taille des échantillons.

Par conséquent, puisque la distribution d’échantillonnage de la différence de moyennes est définie par une distribution normale, la formule pour calculer la statistique de la distribution d’échantillonnage de la différence de moyennes est la suivante :

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Où:

$\overline{x_i}$ est la moyenne de l’échantillon i.
$\mu_i$ est la moyenne de la population i.
$\sigma_i$ est l’écart type de la population i.
$n_i$ est la taille de l’échantillon i.
$Z$ est une variable définie par la distribution normale standard N(0,1).

Notez que les échantillons provenant de différentes populations peuvent avoir des tailles d’échantillon différentes.

Exemple concret de la distribution d’échantillonnage de la différence de moyennes

Une fois que nous aurons vu la définition de la distribution d’échantillonnage de la différence de moyennes et quelle est sa formule, nous allons voir un exemple étape par étape pour finir de comprendre le concept de distribution d’échantillonnage de la différence de moyennes.

Dans une étude statistique, nous souhaitons analyser la différence entre la taille des garçons et des filles d’un certain âge. On sait que la distribution qui définit la population de garçons de cet âge a une moyenne de 157 cm et un écart type de 9 cm et, d’autre part, la distribution qui définit la population de filles de cet âge a une moyenne de 148 cm et un écart type de 7 cm. Si un échantillon de 30 garçons de cet âge et un échantillon de 35 filles de cet âge sont sélectionnés, quelle est la probabilité que la taille moyenne de l’échantillon de garçons soit 12 cm plus grande que la taille moyenne de l’échantillon de filles ?

Pour résoudre ce problème, la première chose à faire est de calculer la statistique de la distribution d’échantillonnage de la différence de moyennes. On applique donc la formule vue ci-dessus :

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right)}=\cfrac{12-(157-148)}{\displaystyle\sqrt{\frac{9^2}{30}+\frac{7^2}{35}}}=1,48$

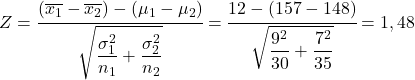
Par conséquent, la probabilité que la taille moyenne de l’échantillon de garçons soit supérieure de 12 cm à la taille moyenne des filles équivaut à la probabilité que la variable Z soit supérieure à 1,48.

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]$

On cherche donc la probabilité de Z>1.48 dans le tableau de Z :

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694$

En bref, la probabilité que la taille moyenne de l’échantillon de garçons soit supérieure de 12 cm à la taille moyenne des filles est de 6,94 %.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus