Distribution d’échantillonnage de la proportion
Cet article explique quelle est la distribution d’échantillonnage de la proportion dans les statistiques. De même, vous trouverez la formule de répartition d’échantillonnage de la proportion et, en plus, un exercice résolu étape par étape.
Quelle est la distribution d’échantillonnage de la proportion ?
La distribution d’échantillonnage de la proportion (ou distribution d’échantillonnage des proportions ) est la distribution qui résulte du calcul de la proportion de chaque échantillon possible d’une population. Autrement dit, les proportions d’échantillonnage de tous les échantillons possibles d’une population forment la distribution d’échantillonnage de la proportion.
En d’autres termes, la distribution d’échantillonnage de la proportion est obtenue en étudiant tous les échantillons pouvant être sélectionnés dans une population et en dérivant la proportion d’échantillonnage de chaque échantillon. Ainsi, l’ensemble des proportions d’échantillon calculées constitue la distribution d’échantillonnage de la proportion.
Au cas où vous vous demanderiez à quoi sert la distribution d’échantillonnage de la proportion, en statistiques, elle est utilisée pour calculer la probabilité d’approcher la valeur de la proportion de population lors de l’analyse d’un seul échantillon.
Formule de distribution d’échantillonnage proportionnel
En fait, lorsque nous étudions une proportion d’un échantillon, nous analysons les cas de réussite. Par conséquent, la variable aléatoire de l’étude suit une distribution de probabilité binomiale .
D’après le théorème central limite, pour les grandes tailles (n>30) on peut rapprocher une distribution binomiale d’une distribution normale. Par conséquent, la distribution d’échantillonnage de la proportion se rapproche d’une distribution normale avec les paramètres suivants :
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f3408076893f390bb65baecfe38e6eff_l3.png)
Où
![]() est la probabilité de succès et
est la probabilité de succès et![]() est la probabilité d’échec
est la probabilité d’échec![]() .
.
Remarque : Une distribution binomiale ne peut être approchée d’une distribution normale que si
![]() ,
,![]() et
et![]() .
.
Par conséquent, puisque la distribution d’échantillonnage de la proportion peut être approchée d’une distribution normale, la formule pour calculer toute probabilité liée à la proportion d’un échantillon est la suivante :

Où:
 est la proportion de l’échantillon.
est la proportion de l’échantillon. est la proportion de la population.
est la proportion de la population. est la probabilité d’échec de la population,
est la probabilité d’échec de la population, .
. est la taille de l’échantillon.
est la taille de l’échantillon. est une variable définie par la distribution normale standard N(0,1).
est une variable définie par la distribution normale standard N(0,1).
Exemple concret de la distribution d’échantillonnage de la proportion
Une fois que nous avons vu la définition de la distribution d’échantillonnage de la proportion et quelles sont ses formules associées, un exemple résolu étape par étape est présenté ci-dessous pour bien comprendre le concept.
- Une entreprise industrielle achète des lots de pièces à une usine qui prétend produire les pièces avec seulement 3 % de pièces défectueuses. Pour le vérifier, l’entreprise décide d’analyser une commande de 500 pièces, quelle est la probabilité de trouver plus de 5% de pièces défectueuses dans l’échantillon ?
Dans ce cas, la proportion de la population que l’on souhaite étudier est de 0,03, donc le paramètre q équivaut à 0,97.
![Rendered by QuickLaTeX.com \begin{array}{c}p=0,03\\[2ex]q=1-p=0,97\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f4354c268853ec7b592bcacd23f3b214_l3.png)
Ainsi, pour trouver la probabilité qu’ils nous demandent, nous devons calculer la statistique correspondante en appliquant la formule que nous avons vue dans la section précédente :
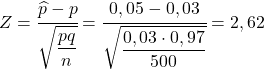
Ainsi la probabilité d’obtenir plus de 5 % de pièces défectueuses équivaut à la probabilité suivante :
![]()
Enfin, nous recherchons la probabilité de P[Z≤2,62] dans le tableau de distribution Z et calculons la probabilité que le problème nous demande :
![Rendered by QuickLaTeX.com \begin{array}{l}P\left[\widehat{p}>0,05\right]=\\[2ex]=P[Z>2,62]=\\[2ex]=1-P[Z\leq 2,62]=\\[2ex]=1-0,9956=\\[2ex]=0,0044\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-812f9b97c53e15da88b0cb7149f254c6_l3.png)
En conclusion, la probabilité de trouver plus de 5 % de pièces défectueuses dans l’échantillon analysé est de 0,44 %.
