Échantillonnage stratifié

Par Pr Amélia Rodriguez août 6, 2023 Statistiques 0 commentaire

Dans cet article, nous expliquons ce qu’est l’échantillonnage stratifié et comment il est réalisé. Vous y trouverez l’explication des sous-types d’échantillonnage stratifié et, enfin, quels sont les avantages et les inconvénients de l’échantillonnage stratifié.

Qu’est-ce que l’échantillonnage stratifié ?

L’échantillonnage stratifié est une méthode statistique utilisée pour sélectionner les éléments d’un échantillon en divisant la population en groupes (appelés strates). Autrement dit, dans l’échantillonnage stratifié, la population est divisée en strates et les individus de chaque strate sont sélectionnés au hasard pour former l’ensemble de l’échantillon d’étude.

Les strates sont des groupes homogènes, ou en d’autres termes, les individus d’une strate ont leurs propres caractéristiques qui les différencient des autres strates. Un individu ne peut donc appartenir qu’à une seule strate.

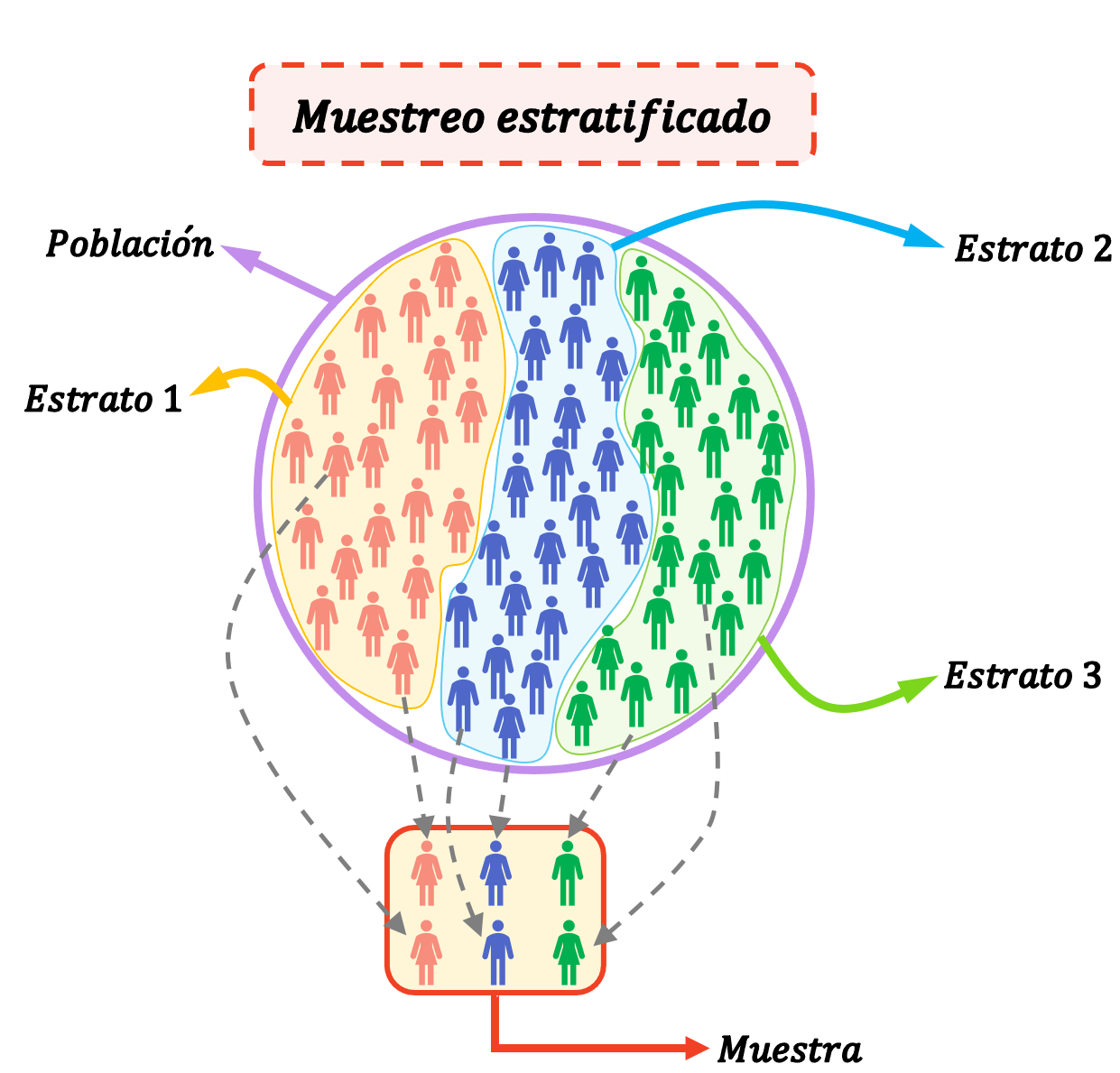
L’échantillonnage stratifié est très utile lorsque la population est composée de groupes très homogènes et très différents les uns des autres.

Logiquement, la somme de la taille de toutes les strates donne la taille de la population statistique :

$N=N_1+N_2+N_3+\dots+N_k$

De même, la somme de la taille de l’échantillon choisi dans chaque strate est égale à la taille totale de l’échantillon de l’étude statistique :

$n=n_1+n_2+n_3+\dots+n_k$

On fait généralement la différence entre les lettres majuscules et minuscules pour désigner respectivement la population ou l’échantillon.

Comment faire un échantillonnage stratifié

Les étapes pour effectuer un échantillonnage stratifié sont les suivantes :

Définir la population cible.
Choisissez la variable de stratification et le nombre de strates qu’il y aura.
Identifiez à quelle strate appartient chaque élément de la population.
Calculez la taille de chaque strate qui fera partie de l’échantillon.
Sélectionnez aléatoirement les éléments de chaque strate qui appartiendront à l’échantillon d’étude. Pour chaque strate, autant d’éléments doivent être sélectionnés que décidé à l’étape précédente.

Gardez à l’esprit que la taille que représentera chaque strate dans l’échantillon dépend non seulement de la taille de la strate, mais également du type d’échantillonnage stratifié. Ensuite, chaque type d’échantillonnage stratifié est expliqué et comment la taille de l’échantillon de chaque strate est calculée à l’aide d’un exemple.

Types d’échantillonnage stratifié

Maintenant que vous connaissez la définition de l’échantillonnage stratifié, vous devez savoir qu’il existe plusieurs types d’échantillonnage stratifié, qui sont classés comme suit :

Échantillonnage stratifié proportionnel
Échantillonnage stratifié uniforme
L’échantillonnage est optimal

Chaque type d’échantillonnage stratifié est expliqué en détail ci-dessous pour mieux comprendre la signification de chacun.

Échantillonnage stratifié proportionnel

Dans l’échantillonnage stratifié proportionnel , ou échantillonnage avec répartition proportionnelle, le nombre d’éléments de chaque strate qui font partie de l’échantillon d’étude est proportionnel à la taille de chaque strate.

Ainsi, si une strate est plus grande qu’une autre, l’échantillon final contiendra davantage d’éléments provenant de cette strate. En revanche, si une strate est plus petite qu’une autre, il y aura moins d’éléments de cette strate dans l’échantillon d’analyse statistique.

Ce type d’échantillonnage stratifié est utile lorsque les strates sont de tailles différentes et que nous souhaitons que l’échantillon comprenne davantage d’éléments provenant des strates plus grandes.

Pour calculer le nombre d’éléments de chaque strate qui feront partie de l’échantillon, la taille de chaque strate doit être divisée par la somme des tailles de toutes les strates. Le résultat sera la proportion de la strate qui devrait être incluse dans l’échantillon, elle devra donc être multipliée par la taille d’échantillon souhaitée.

$n_i=n\cdot \cfrac{N_i}{N_1+N_2+\dots +N_k}=n\cdot \cfrac{N_i}{N}$

Où

$n$ est la taille totale de l’échantillon souhaité, $n_i$ le nombre d’éléments dans la strate $i$ à inclure dans l’échantillon, $N_i$ taille de la strate $i$ , et $N$ le nombre total d’éléments dans la population.

Par exemple, imaginez que nous voulions faire une étude dans une entreprise de 150 travailleurs, en prenant un échantillon de 50 personnes et en stratifiant les données en fonction de l’âge des travailleurs. Nous pouvons classer les données comme suit :

De 20 à 29 ans : 35 ouvriers
De 30 à 39 ans : 57 salariés
De 40 à 49 ans : 42 salariés
De 50 à 59 ans : 16 salariés

Ainsi, si l’on stratifie les données proportionnellement, l’échantillonnage sera le suivant :

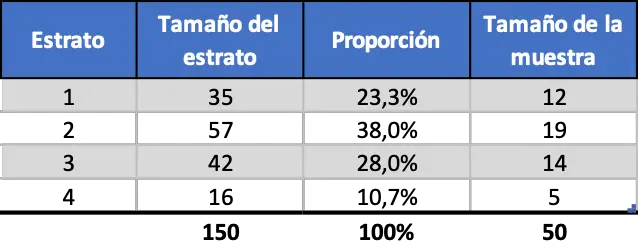
Échantillonnage stratifié uniforme

Dans l’échantillonnage stratifié uniforme , ou échantillonnage par affixation uniforme, le nombre d’éléments de chaque strate qui fait partie de l’échantillon d’étude est égal.

Chaque strate a donc le même poids dans ce type d’échantillonnage. Qu’une strate compte plus ou moins d’individus qu’une autre strate, tous seront représentés dans l’échantillon par le même nombre d’individus.

Dans ce cas, pour calculer la taille des éléments dans chaque strate, la taille d’échantillon souhaitée doit être divisée par le nombre de strates existantes. Autrement dit, la formule suivante doit être utilisée :

$n_i=\cfrac{n}{k}$

Où

$n$ est la taille totale de l’échantillon souhaité, $n_i$ le nombre d’éléments dans la strate $i$ qui sera inclus dans l’échantillon, et $k$ le nombre de strates dans lesquelles la population a été divisée.

En suivant l’exemple précédent, puisque nous voulions un échantillon de 50 travailleurs et qu’au total il y avait 4 strates différentes, la taille de l’échantillon de chaque strate sera :

$n_i=\cfrac{50}{4}=12,5$

Le résultat étant un nombre décimal, certaines strates auront 12 travailleurs et d’autres 13 jusqu’à atteindre 50 travailleurs. De sorte que l’échantillonnage stratifié uniforme est le suivant :

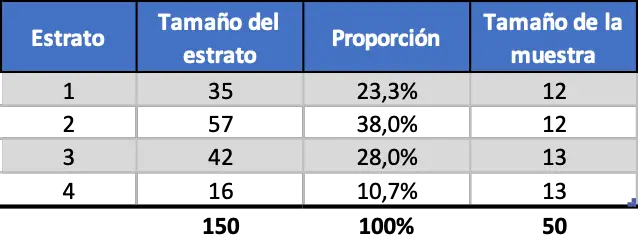
Comme vous pouvez le constater, la taille de l’échantillon de chaque strate est indépendante de la proportion de chacune.

Échantillonnage stratifié optimal

Dans l’échantillonnage stratifié optimal , le nombre d’éléments dans chaque strate dépend proportionnellement de la variabilité de chaque strate.

Ainsi, les strates avec une plus grande variabilité auront une taille d’échantillon plus grande, et vice versa, les strates avec moins de variabilité auront une taille d’échantillon plus petite.

La formule permettant de déterminer combien d’éléments de chaque strate feront partie de l’échantillon de l’étude statistique est la suivante :

$n_i=n\cdot \cfrac{\sigma_i\cdot N_i}{\displaystyle \sum_{j=1}^k \sigma_j\cdot N_j }$

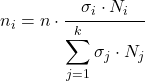
Où

$n$ est la taille totale de l’échantillon souhaité, $n_i$ est le nombre d’éléments dans la strate $i$ à inclure dans l’échantillon, $\sigma_i$ est l’écart type (ou écart typique) de la strate $i$ , et $N_i$ est la taille de la strate $i$ .

Avantages et inconvénients de l’échantillonnage stratifié

L’échantillonnage stratifié présente les avantages et les inconvénients suivants :

avantage	Désavantages
Il permet d’étudier statistiquement non seulement l’ensemble de la population, mais également chaque strate particulière.	C’est une méthode d’échantillonnage compliquée à mettre en œuvre.
L’erreur d’échantillonnage commise par l’échantillonnage stratifié est toujours égale ou inférieure à celle de l’échantillonnage aléatoire simple.	Il s’agit d’un échantillonnage qui prend beaucoup de temps et coûte donc cher.
Il permet de profiter des connaissances du chercheur sur la population.	De nombreuses informations sont nécessaires sur l’échantillon analysé pour pouvoir le stratifier.
Avec l’échantillonnage stratifié, nous garantissons qu’au moins un élément de chaque strate est inclus dans l’échantillon.	Il est nécessaire de connaître la proportion de chaque strate pour pouvoir faire l’échantillonnage.

La principale caractéristique de l’échantillonnage stratifié est qu’il est utilisé pour analyser statistiquement chaque groupe ou strate dans lequel la population a été divisée. Bien entendu, l’ensemble de la population peut également être étudiée avec ce type d’échantillonnage. De plus, la stratification des données produira d’autant plus d’avantages que les strates seront différentes les unes des autres.

Au contraire, le fait de stratifier les données pour pouvoir réaliser l’échantillonnage implique une augmentation de la complexité de l’échantillonnage, l’échantillonnage stratifié étant plus compliqué à réaliser par rapport à d’autres types d’échantillonnage. Cette propriété implique également qu’il s’agit d’un échantillon coûteux à réaliser, car il faut du temps pour effectuer correctement la stratification.

Un autre inconvénient de l’échantillonnage stratifié est qu’il nécessite beaucoup d’informations sur la population que l’on souhaite étudier, ce qui n’est pas nécessaire dans d’autres types d’échantillonnage comme l’échantillonnage aléatoire simple. Bien que cet inconvénient puisse être atténué si le chercheur possède de grandes connaissances dans le domaine.

Enfin, avec l’échantillonnage stratifié, on obtient un échantillon plus représentatif de la population que dans les autres types d’échantillonnage, car on s’assure d’inclure des éléments de chaque strate. En revanche, dans d’autres échantillons, l’échantillon résultant peut ne contenir aucun élément d’aucune strate.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus