Échantillonnage systématique
Dans cet article, nous expliquons ce qu’est l’échantillonnage systématique, ses caractéristiques et comment il est réalisé. Vous verrez également un exemple d’échantillonnage systématique. De plus, vous découvrirez quels sont les avantages et les inconvénients de l’échantillonnage systématique et quand ce type d’échantillonnage doit être utilisé.
Qu’est-ce que l’échantillonnage systématique ?
L’échantillonnage systématique est une méthode probabiliste utilisée pour sélectionner les éléments qui feront partie de l’échantillon d’une étude statistique. Dans l’échantillonnage systématique, un élément est d’abord sélectionné au hasard, et les autres éléments de l’échantillon sont sélectionnés selon un intervalle fixe.
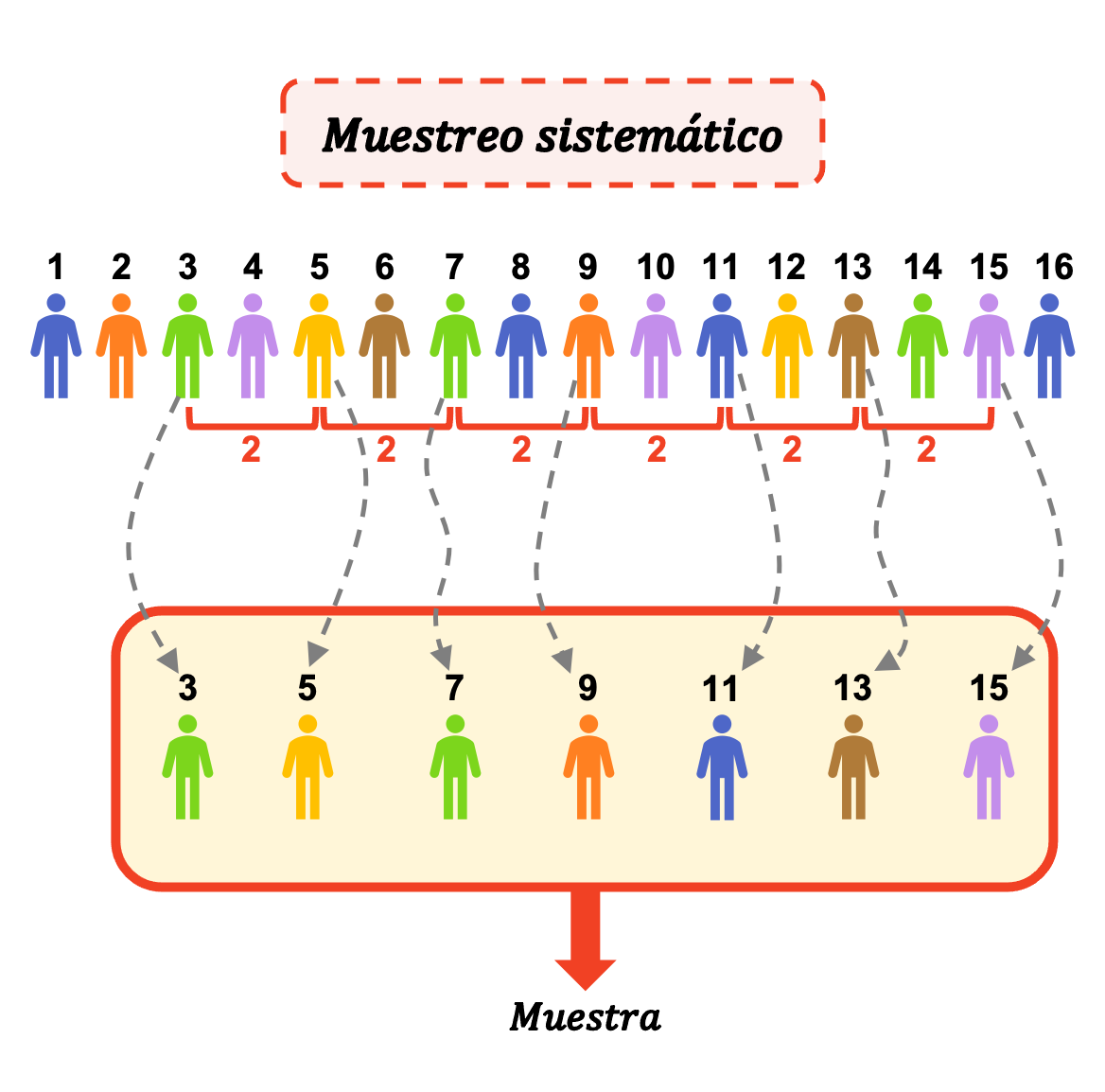
Par conséquent, dans l’échantillonnage systématique, une fois que nous avons sélectionné au hasard le premier individu de l’échantillon, nous devons compter autant de nombres que l’intervalle souhaité pour prendre l’individu suivant de l’échantillon. Et nous répétons successivement la même procédure jusqu’à avoir autant d’individus dans l’échantillon que la taille d’échantillon que nous souhaitons obtenir.
En revanche, il faut savoir qu’il existe davantage de méthodes pour sélectionner des individus à partir d’un échantillon. Les types d’échantillonnage les plus utilisés sont :
- Échantillonnage aléatoire simple
- échantillonnage stratifié
- échantillonnage systématique
- Échantillonnage en grappes
Sur probabilistica.com, nous avons une explication détaillée de chaque type d’échantillonnage probabiliste, donc si vous êtes plus intéressé, vous pouvez rechercher comment chacun d’eux est effectué sur notre site Web.
Comment faire un échantillonnage systématique
Les étapes pour effectuer un échantillonnage aléatoire systématique sont les suivantes :
- Définir la population cible.
- Déterminez la taille de l’échantillon souhaitée.
- Calculez l’ intervalle d’échantillonnage . Pour ce faire, la taille de la population est divisée par la taille de l’échantillon.
- Sélectionnez au hasard le premier élément de l’échantillon.
- Sélectionnez les éléments restants de l’échantillon. Pour ce faire, l’intervalle d’échantillonnage est successivement ajouté au nombre sélectionné à l’étape précédente.
Il est important que le premier élément sélectionné dans un échantillonnage systématique soit aléatoire, car c’est en réalité le seul élément de l’échantillon qui est sélectionné aléatoirement. Autrement, le caractère aléatoire de l’échantillonnage systématique serait compromis. C’est pourquoi le chercheur doit garantir que tous les éléments de la population ont la même probabilité d’être sélectionnés comme point de départ.
De même, étant donné que les éléments de l’échantillon dans l’échantillonnage systématique sont sélectionnés par intervalles, il se peut qu’il n’y ait pas d’élément d’un certain type dans l’échantillon final et, par conséquent, l’échantillon peut ne pas être suffisamment représentatif. Mais c’est un risque que l’on court lorsqu’on procède à un échantillonnage systématique.
Enfin, vous devez tenir compte du fait que l’intervalle d’échantillonnage n’est pas un modèle, car alors l’échantillon sélectionné ne sera pas adéquat et l’étude statistique donnera des résultats peu fiables.
Exemple d’échantillonnage systématique
Après avoir vu la définition de l’échantillonnage systématique, nous allons vous expliquer un exemple de ce type d’échantillonnage afin que vous compreniez mieux sa signification.
Par exemple, si l’on souhaite effectuer un échantillonnage systématique sur une population de 1000 éléments pour obtenir un échantillon de 50 éléments, il faut procéder comme suit.
Tout d’abord, nous devons calculer l’intervalle d’échantillonnage. Pour ce faire, nous divisons simplement la taille de la population par la taille de l’échantillon :
![]()
Deuxièmement, nous devons sélectionner au hasard le premier sujet de l’échantillon. Pour réaliser cette étape, il existe plusieurs méthodes, mais vous pouvez utiliser, par exemple, le programme informatique Excel pour obtenir un nombre aléatoire de 1 à 20 (il est recommandé que le premier nombre soit dans le premier fragment). Supposons que nous obtenions le numéro 17.
![]()
Ensuite, nous devons ajouter l’intervalle d’échantillonnage (20) au nombre 17 pour sélectionner les éléments suivants de l’échantillon. Nous devons sélectionner 49 nombres supplémentaires, puisque la taille d’échantillon souhaitée est de 50.
![]()
De sorte que les éléments de la population qui s’identifient aux chiffres qui sont sortis sont ceux sélectionnés pour faire partie de l’échantillon de l’étude statistique.
Avantages et inconvénients de l’échantillonnage systématique
L’échantillonnage systématique présente les avantages et les inconvénients suivants :
| avantage | Désavantages |
|---|---|
| L’échantillonnage systématique est très rapide à réaliser. | S’il existe un modèle et qu’il correspond à l’intervalle d’échantillonnage, vous obtiendrez un échantillon biaisé. |
| C’est facile à comprendre. | Dans l’échantillon sélectionné, il n’y a qu’un seul élément choisi au hasard. |
| Les échantillons obtenus sont généralement représentatifs. | Une fois le sujet initial sélectionné, certains éléments ont une probabilité nulle d’être sélectionnés. |
| L’échantillonnage systématique ne se limite pas à une partie de la population, mais échantillonne plutôt des éléments répartis dans toute la population. | L’estimation des variations est plus compliquée que dans le système d’échantillonnage aléatoire simple. |
Comme nous l’avons vu dans l’exemple ci-dessus, l’échantillonnage systématique est rapide et facile à réaliser. Même si cela ne semble pas être le cas, cette propriété est importante car elle implique un coût économique moindre.
Un autre aspect positif de l’échantillonnage systématique est qu’il prélève des éléments sur l’ensemble de la population. En revanche, dans d’autres types d’échantillonnage, on pourrait par exemple prendre des éléments uniquement de la première moitié de la population.
Un inconvénient de l’échantillonnage systématique est que l’ordre dans lequel les éléments de la population sont placés peut conditionner la fiabilité des résultats statistiques, car s’il existe un certain type de périodicité ou de modèle, un échantillon biaisé pourrait être obtenu. Par exemple, si l’on ordonne une population d’hommes et de femmes comme suit :
![]()
Avec cet ordre, si l’on prend un intervalle d’échantillonnage de 2, on sélectionnera uniquement des femmes ou uniquement des hommes selon le point d’origine. Par conséquent, nous obtiendrons un échantillon peu fiable.
Enfin, un autre aspect négatif de l’échantillonnage systématique est qu’un seul élément est sélectionné au hasard, ce qui conditionne le reste des éléments de l’échantillon. Contrairement à d’autres types d’échantillonnage dans lesquels le hasard est beaucoup plus présent tout au long de la procédure.
Quand utiliser l’échantillonnage systématique
Enfin, nous vous montrons quand il est pratique d’utiliser l’échantillonnage systématique et quand ce n’est pas le cas, puisque ce système d’échantillonnage ne peut pas toujours être utilisé.
L’échantillonnage systématique peut être utilisé lorsqu’une méthode d’échantillonnage simple et rapide à mettre en œuvre est nécessaire. Autrement dit, lorsque le budget du projet est limité, l’échantillonnage systématique est une très bonne option car il nécessite peu de ressources pour le réaliser.
Comme nous l’avons vu tout au long de l’article, il n’est pas pratique d’utiliser ce type d’échantillonnage lorsque la population présente un certain type de modèle, car un échantillon biaisé pourrait être obtenu.
Enfin, s’il existe de nombreux groupes différents dans la population, ou en d’autres termes, si elle comporte de nombreuses strates, il est préférable d’utiliser l’échantillonnage stratifié car il permet une analyse statistique des strates séparément, ce que ne permet pas l’échantillonnage systématique.
