Que sont les événements disjoints ? (Définition & Exemples)

Les événements disjoints sont des événements qui ne peuvent pas se produire en même temps.

Écrits en notation probabiliste, les événements A et B sont disjoints si leur intersection est nulle. Cela peut s’écrire comme suit :

• P(A et B) = 0
• P(UNE∩B) = 0

Par exemple, supposons que nous sélectionnions une carte au hasard dans un jeu. Soit l’événement A l’événement selon lequel la carte est un pique ou un trèfle et que l’événement B soit l’événement selon lequel la carte est un cœur ou un diamant.

Nous définirions l’ espace échantillon pour les événements comme suit :

• A = {Pique, Trèfle}
• B = {Cœur, Diamant}

Notez qu’il n’y a pas de chevauchement entre les deux espaces échantillonnés. Ainsi, les événements A et B sont des événements disjoints car ils ne peuvent pas se produire tous les deux en même temps.

Remarque : les événements disjoints sont également dits s’excluant mutuellement .

Exemples d’événements disjoints

Voici quelques exemples supplémentaires d’événements disjoints.

Exemple 1 : tirage au sort

Supposons que vous tiriez à pile ou face. Soit l’événement A l’événement où la pièce atterrit sur face et l’événement B l’événement où la pièce atterrit sur face.

L’événement A et l’événement B seraient disjoints car ils ne peuvent pas se produire tous les deux en même temps. La pièce ne peut pas atterrir sur pile ou face.

Exemple 2 : lancer de dés

Supposons que vous lancez un dé. Soit l’événement A l’événement où le dé atterrit sur un nombre impair et soit l’événement B l’événement où le dé atterrit sur un nombre pair.

L’événement A et l’événement B seraient disjoints car ils ne peuvent pas se produire tous les deux en même temps. Les dés ne peuvent pas tomber sur un nombre pair et sur un nombre impair.

Exemple 3 : Emplacement du Pro Bowl

Supposons que la NFL veuille choisir un emplacement pour accueillir le Pro Bowl. Ils ont réduit les options à Miami et San Diego. Ils placent les deux noms dans un chapeau et en choisissent un au hasard. Supposons que l’événement A soit l’événement pour lequel ils sélectionnent Miami et que l’événement B soit l’événement pour lequel ils sélectionnent San Diego.

L’événement A et l’événement B seraient disjoints car ils ne peuvent pas se produire tous les deux en même temps. Miami et San Diego ne peuvent pas être sélectionnés tous les deux.

Visualiser des événements disjoints

Un moyen utile de visualiser des événements disjoints consiste à créer un diagramme de Venn.

Si deux événements sont disjoints , ils ne se chevaucheront pas du tout dans un diagramme de Venn :

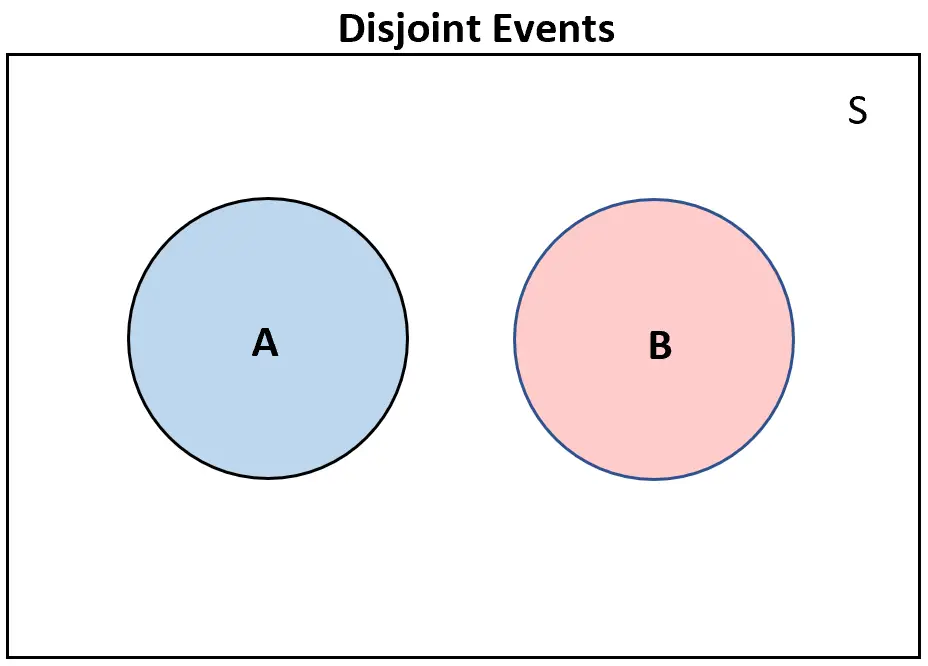
À l’inverse, si deux événements ne sont pas disjoints , il y aura au moins un certain chevauchement dans le diagramme de Venn :

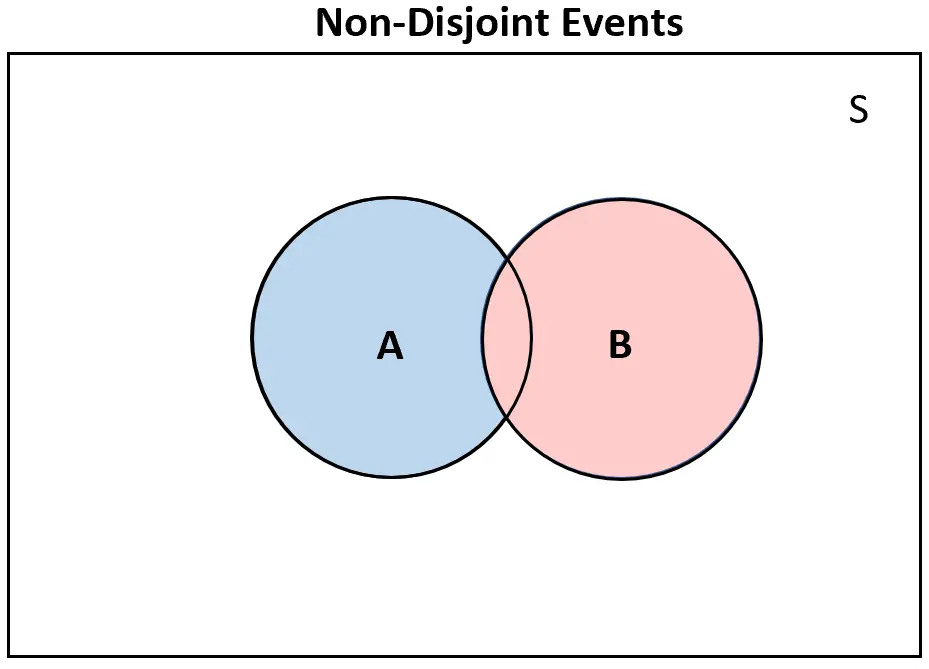
La probabilité d’événements disjoints

Comme mentionné précédemment, si deux événements sont disjoints, la probabilité qu’ils se produisent tous les deux en même temps est nulle.

• P(UNE∩B) = 0

De même, la probabilité que l’un ou l’autre événement se produise peut être calculée en additionnant leurs probabilités individuelles.

• P(UNE∪B) = P(UNE) + P(B)

Par exemple, laissez l’événement A être l’événement où un dé atterrit sur un 1 ou un 2 et laissez l’événement B être l’événement où un dé atterrit sur un 5 ou un 6.

Nous définirions l’espace échantillon pour les événements comme suit :

• UNE = {1, 2}
• B = {5, 6}

Nous calculerions la probabilité que l’événement A ou l’événement B se produise comme :

• P(UNE∪B) = P(UNE) + P(B)
• P(UNE∪B) = 2/6 + 2/6
• P(UNE∪B) = 4/6 = 2/3

La probabilité que l’événement A ou l’événement B se produise est de 2/3 .

Ressources additionnelles

Les didacticiels suivants fournissent des explications sur d’autres sujets courants en probabilité :

Comment trouver la probabilité de A ou B : avec des exemples
Comment trouver la probabilité de A et B : avec des exemples
Loi de probabilité totale : définition et exemples