Excel : comment utiliser LINEST pour effectuer une régression linéaire multiple

Vous pouvez utiliser la fonction LINEST dans Excel pour ajuster un modèle de régression linéaire multiple à un ensemble de données.

Cette fonction utilise la syntaxe de base suivante :

=LINEST(known_y's, [known_x's], [const], [stats])

où:

• known_y’s : un tableau de valeurs y connues
• known_x’s : un tableau de valeurs x connues
• const : Argument facultatif. Si VRAI, la constante b est traitée normalement. Si FALSE, la constante b est définie sur 1.
• stats : Argument facultatif. Si VRAI, des statistiques de régression supplémentaires sont renvoyées. Si FALSE, les statistiques de régression supplémentaires ne sont pas renvoyées.

L’exemple suivant, étape par étape, montre comment utiliser cette fonction dans la pratique.

Étape 1 : Saisissez les données

Tout d’abord, entrons l’ensemble de données suivant dans Excel :

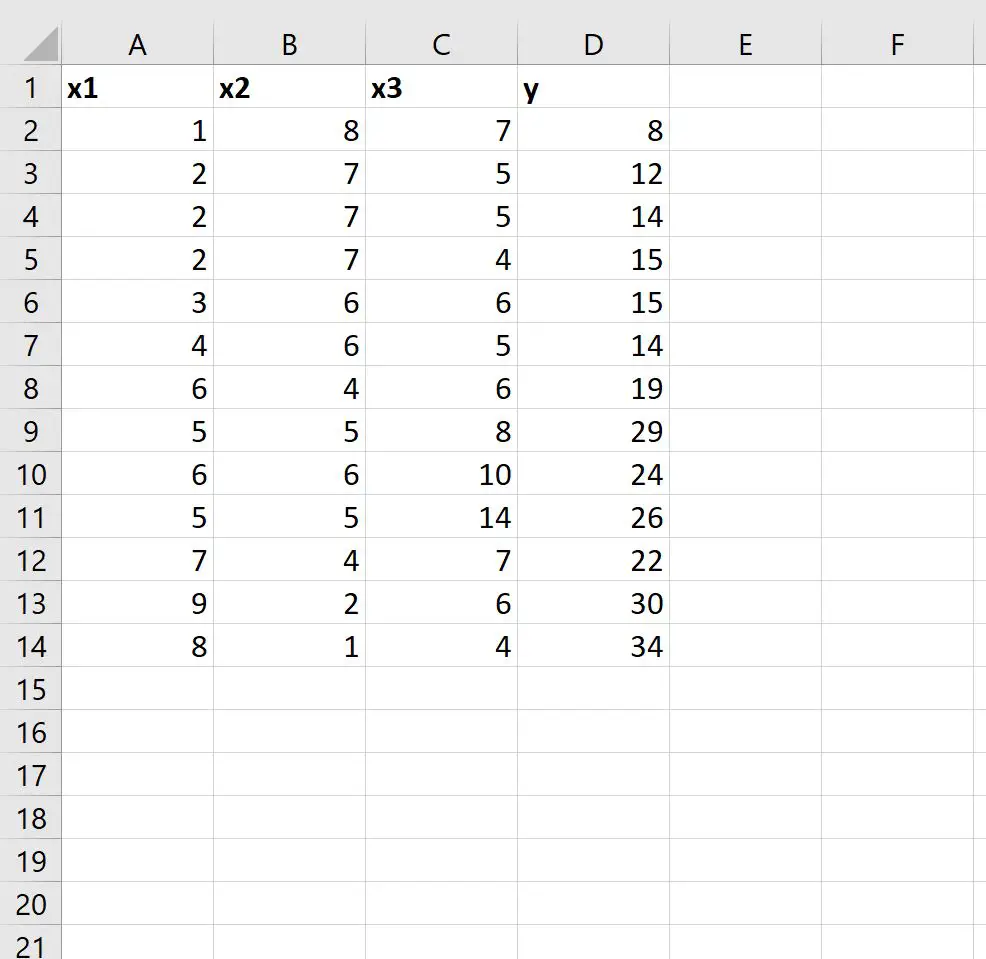
Étape 2 : utilisez LINEST pour ajuster un modèle de régression linéaire multiple

Supposons que nous souhaitions ajuster un modèle de régression linéaire multiple en utilisant x1 , x2 et x3 comme variables prédictives et y comme variable de réponse.

Pour ce faire, nous pouvons taper la formule suivante dans n’importe quelle cellule pour l’adapter à ce modèle de régression linéaire multiple

=LINEST(D2:D14, A2:C14)

La capture d’écran suivante montre comment utiliser cette formule en pratique :

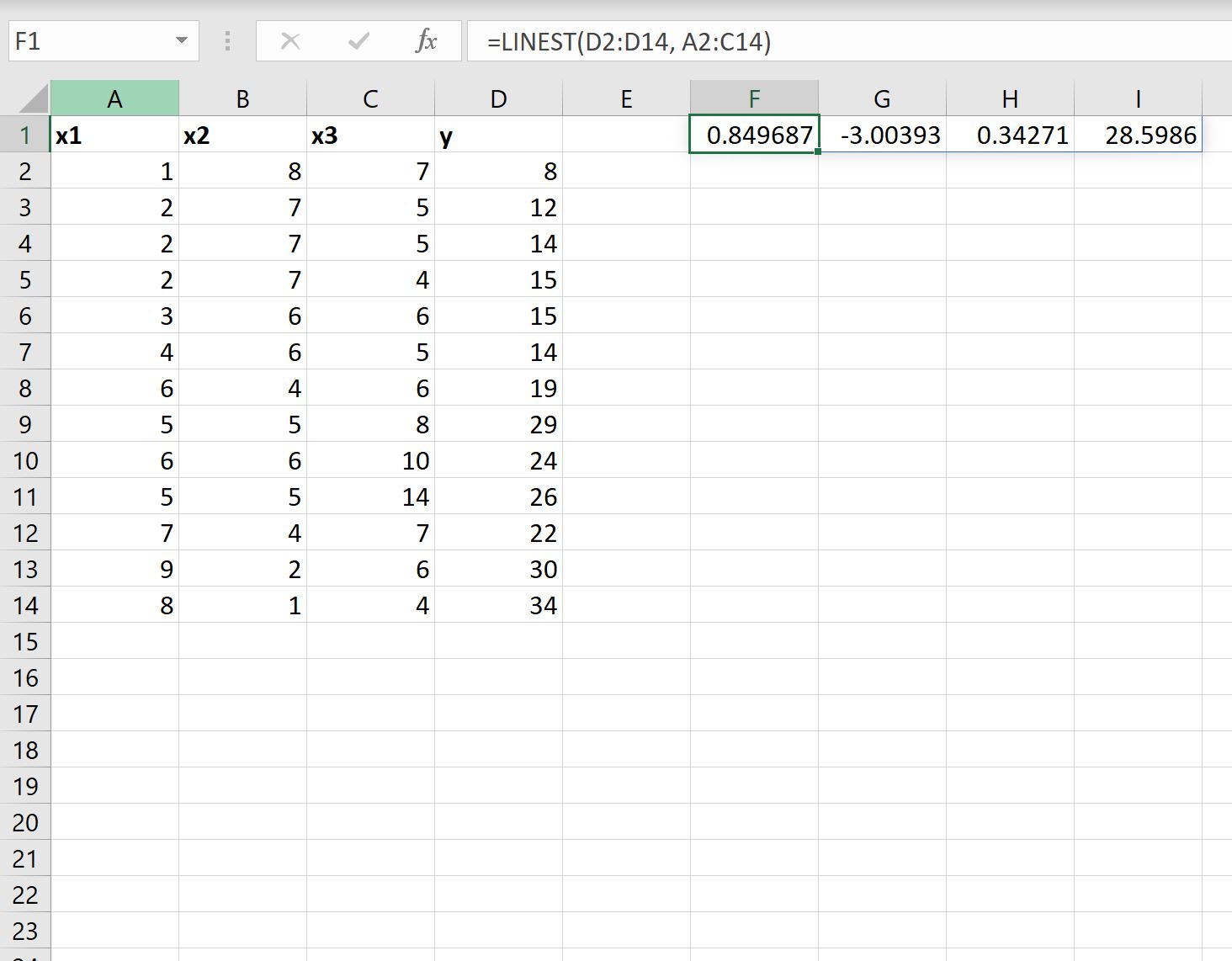
Voici comment interpréter le résultat :

• Le coefficient de l’ordonnée à l’origine est 28,5986 .
• Le coefficient pour x1 est 0,34271 .
• Le coefficient pour x2 est -3,00393 .
• Le coefficient pour x3 est 0,849687 .

En utilisant ces coefficients, nous pouvons écrire l’équation de régression ajustée comme suit :

y = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)

Étape 3 (Facultatif) : Afficher des statistiques de régression supplémentaires

Nous pouvons également définir la valeur de l’argument stats dans la fonction LINEST égale à TRUE pour afficher des statistiques de régression supplémentaires pour l’équation de régression ajustée :

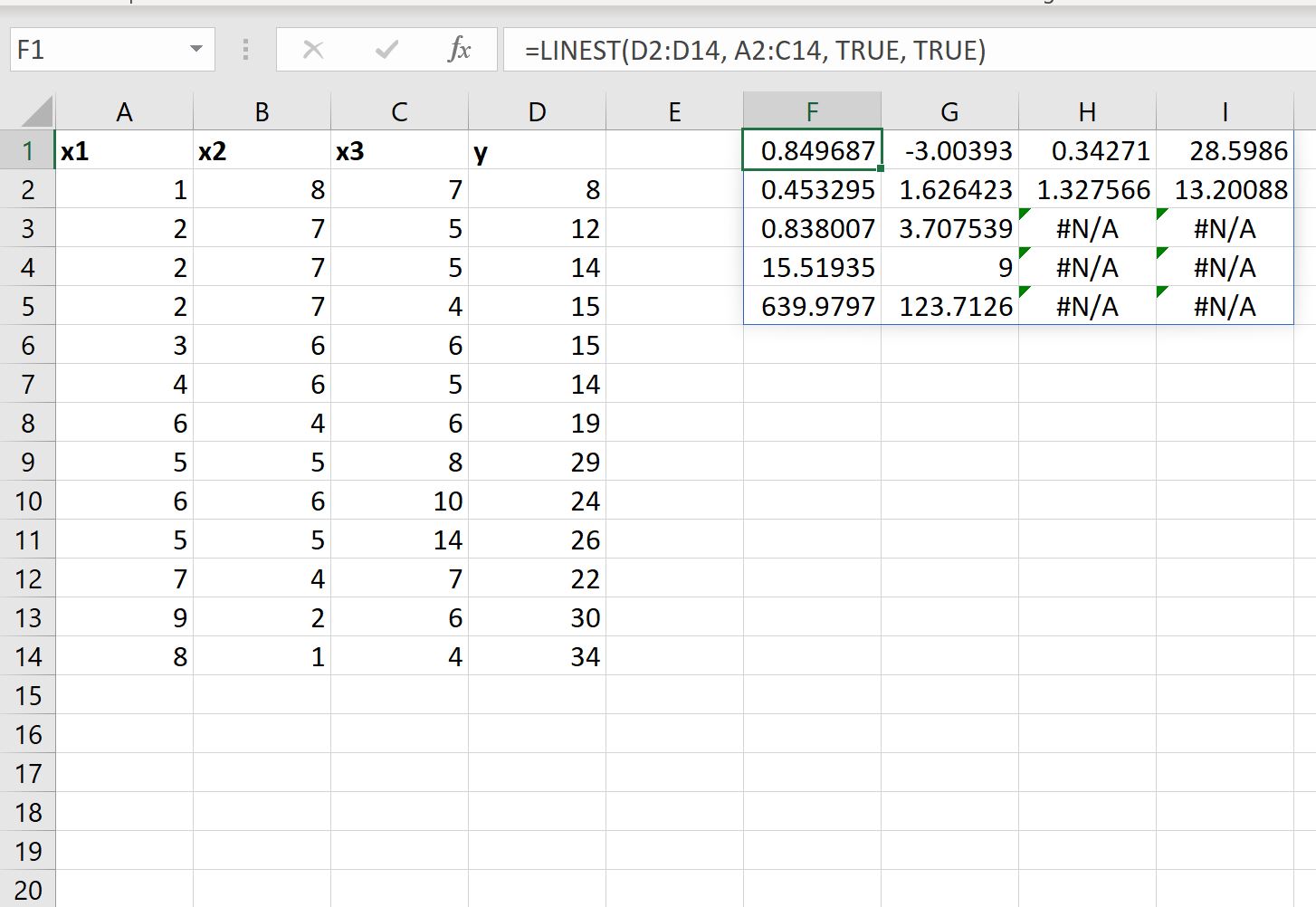
L’équation de régression ajustée est toujours la même :

y = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)

Voici comment interpréter les autres valeurs du résultat :

• L’erreur standard pour x3 est 0,453295 .
• L’erreur standard pour x2 est 1,626423 .
• L’erreur standard pour x1 est 1,327566 .
• L’erreur standard pour l’interception est 13.20088 .
• Le R ² du modèle est .838007 .
• L’erreur type résiduelle pour y est 3,707539 .
• La statistique F globale est de 15,51925 .
• Les degrés de liberté sont 9 .
• La somme des carrés de régression est 639,9797 .
• La somme résiduelle des carrés est 123,7126 .

En général, la mesure la plus intéressante dans ces statistiques supplémentaires est la valeur R ² , qui représente la proportion de la variance de la variable de réponse qui peut être expliquée par la variable prédictive.

La valeur de R ² peut varier de 0 à 1.

Puisque le R ² de ce modèle particulier est de 0,838 , cela nous indique que les variables prédictives réussissent bien à prédire la valeur de la variable de réponse y.

Connexes : Qu’est-ce qu’une bonne valeur R au carré ?

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres opérations courantes dans Excel :

Comment utiliser la fonction LOGEST dans Excel
Comment effectuer une régression non linéaire dans Excel
Comment effectuer une régression cubique dans Excel