Excel : comment interpréter la sortie de la fonction LINEST

Vous pouvez utiliser la fonction LINEST pour ajuster un modèle de régression dans Excel.

Cette fonction utilise la syntaxe de base suivante :

LINEST(known_y's, known_x's, const, stats)

où:

• known_y’s : une colonne de valeurs pour la variable de réponse
• known_x’s : une ou plusieurs colonnes de valeurs pour les variables prédictives
• const : TRUE = calculer l’interception normalement, FALSE = forcer l’interception à zéro
• stats : TRUE = calculer des statistiques de régression supplémentaires, FALSE = calculer uniquement les coefficients

L’exemple suivant montre comment interpréter la sortie de la fonction LINEST dans la pratique.

Exemple : Comment interpréter la sortie LINEST dans Excel

Supposons que nous ayons l’ensemble de données suivant qui contient une variable prédictive (x) et une variable de réponse (y) :

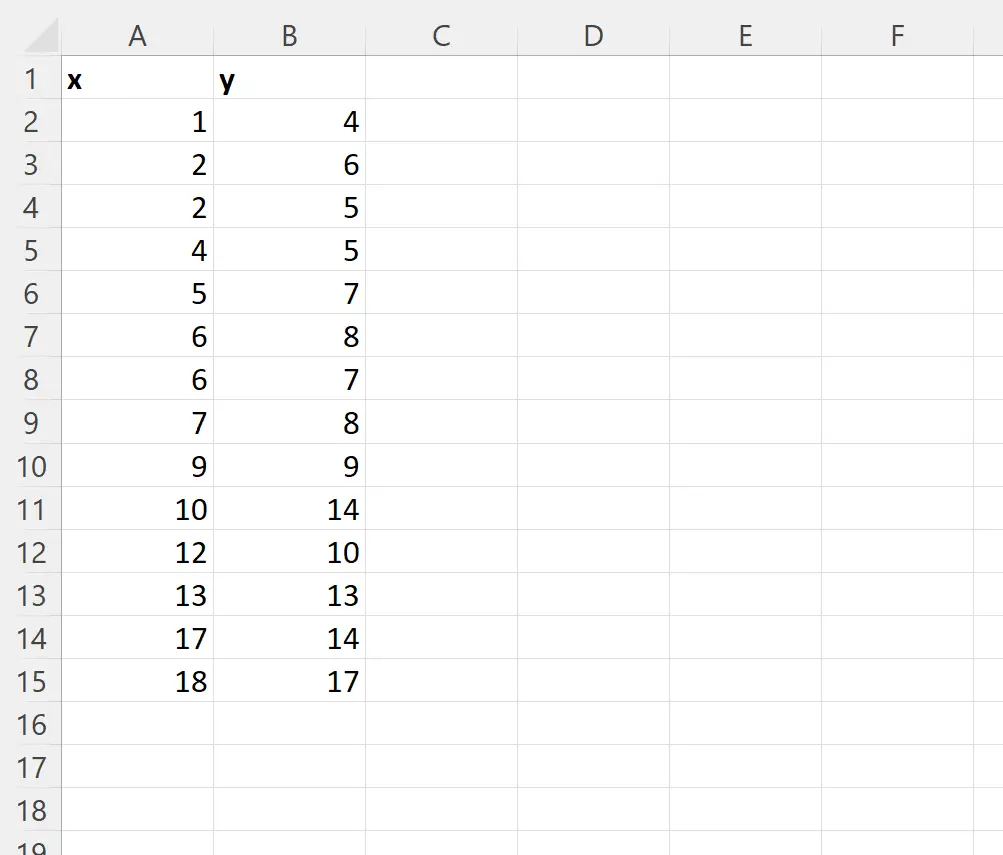
Nous pouvons taper la formule suivante dans la cellule D1 pour effectuer une régression linéaire simple avec cet ensemble de données :

=LINEST(A2:A15, B2:B15, TRUE, TRUE)

La sortie de la fonction LINEST contient les coefficients du modèle de régression ainsi que plusieurs statistiques supplémentaires :

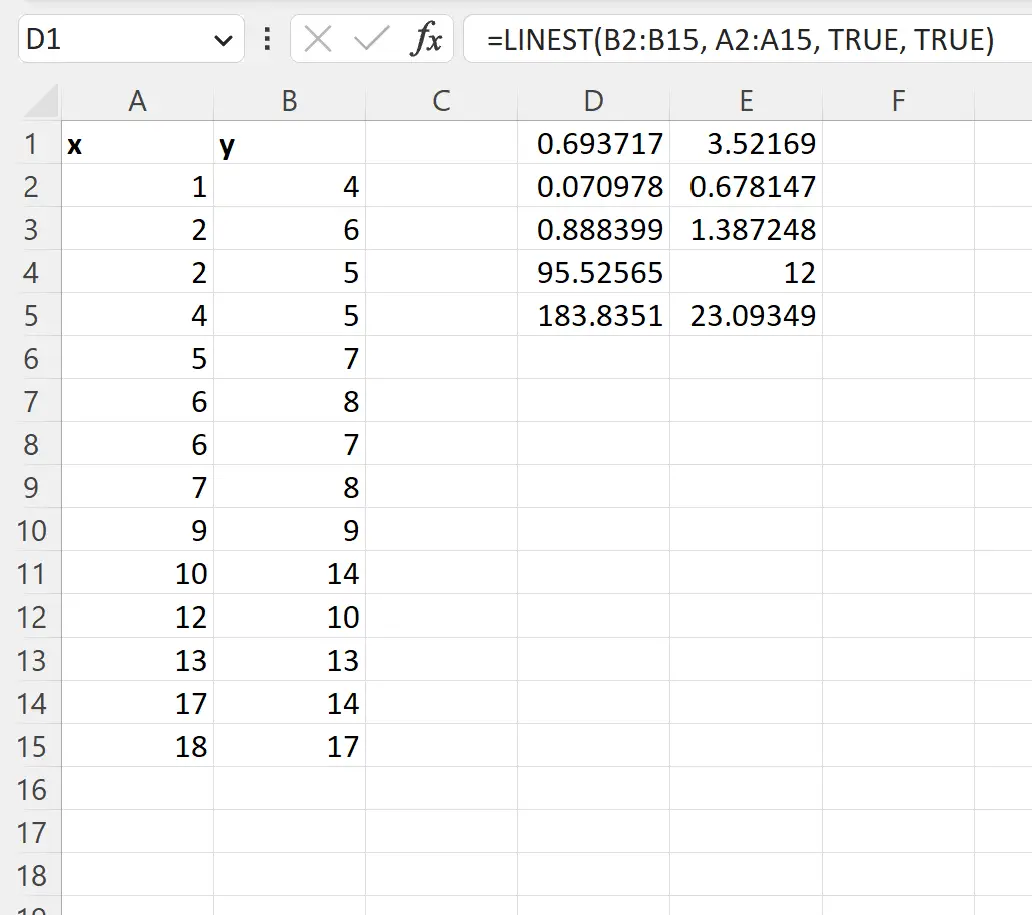
La capture d’écran suivante fournit une explication de chaque valeur dans le résultat :

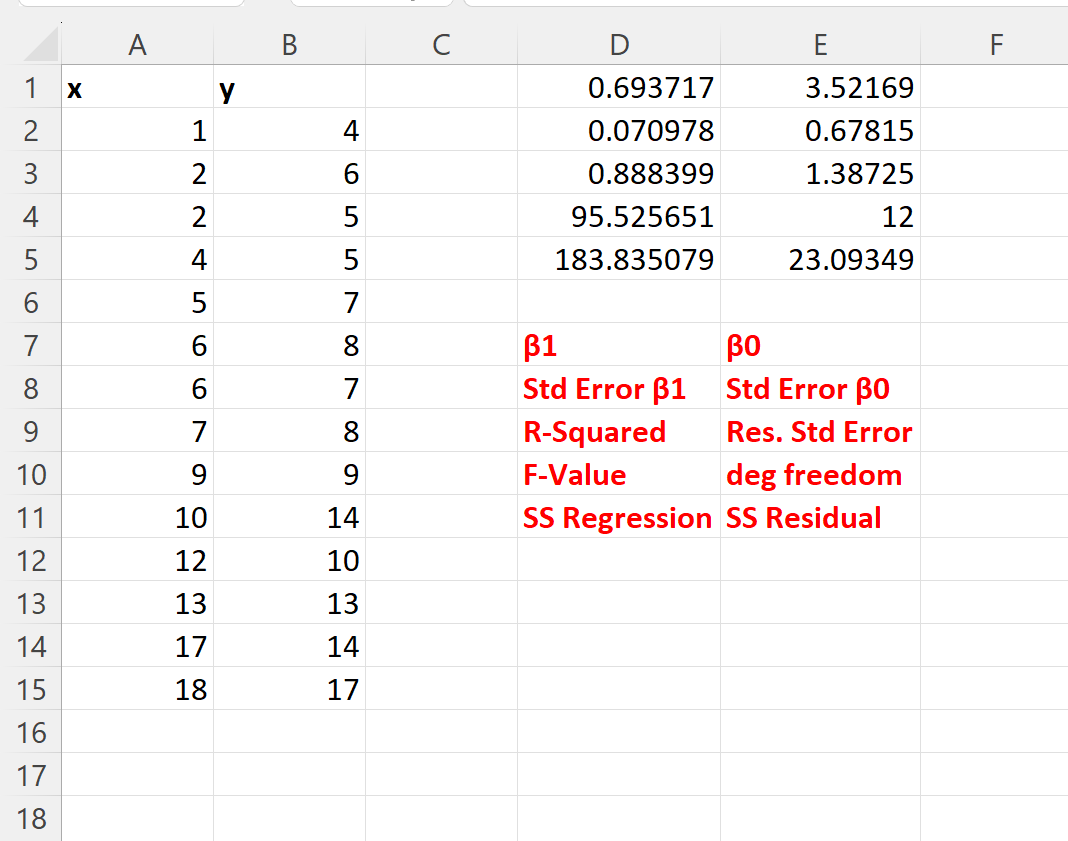
À partir du résultat, nous pouvons voir :

• Le coefficient pour β ₀ est 3,52169 .
• Le coefficient pour β ₁ est 0,693717 .

En utilisant ces valeurs, nous pouvons écrire l’équation de ce modèle de régression simple :

y = 3,52169 + 0,693717(x)

Nous interprétons cela comme signifiant que chaque augmentation supplémentaire d’une unité de la variable prédictive x est associée à une augmentation moyenne de 0,693717 de la variable de réponse y.

Nous interprétons le terme d’origine comme signifiant que lorsque x est égal à zéro, la valeur moyenne de y est 3,52169 .

On peut également voir :

• La valeur R au carré du modèle est de 0,888 .

Nous interprétons cela comme signifiant que la variable prédictive est capable d’expliquer 88,8 % de la variation de la variable de réponse du modèle.

Connexes : Qu’est-ce qu’une bonne valeur R au carré ?

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur la régression dans Excel :

Comment interpréter les valeurs P dans la sortie de régression dans Excel
Comment ajouter une ligne de régression à un nuage de points dans Excel
Comment effectuer une régression polynomiale dans Excel