Comment effectuer un test t avec des variances inégales dans Excel

Un test t à deux échantillons est utilisé pour déterminer si les moyennes de deux populations sont égales ou non.

Il existe deux versions des deux exemples de test t que vous pouvez utiliser :

• test t avec variances égales
• test t avec variances inégales

Nous utilisons un test t avec des variances inégales lorsque les variances des deux échantillons ne sont pas égales.

Le moyen le plus simple de déterminer si les variances entre les deux échantillons sont égales est d’utiliser la règle empirique de la variance .

En règle générale, si le rapport entre la plus grande variance et la plus petite variance est inférieur à 4, nous pouvons supposer que les variances sont à peu près égales.

Sinon, si le rapport est égal ou supérieur à 4, on suppose que les variances ne sont pas égales.

L’exemple étape par étape suivant montre comment effectuer un test t à deux échantillons avec des variances inégales dans Excel.

Étape 1 : Saisissez les données

Supposons que nous souhaitions déterminer si deux méthodes d’étude différentes conduisent à des résultats moyens différents aux examens parmi les étudiants d’une université donnée.

Nous sélectionnons un échantillon aléatoire de 20 étudiants pour utiliser chaque méthode d’étude et enregistrons leurs résultats aux examens :

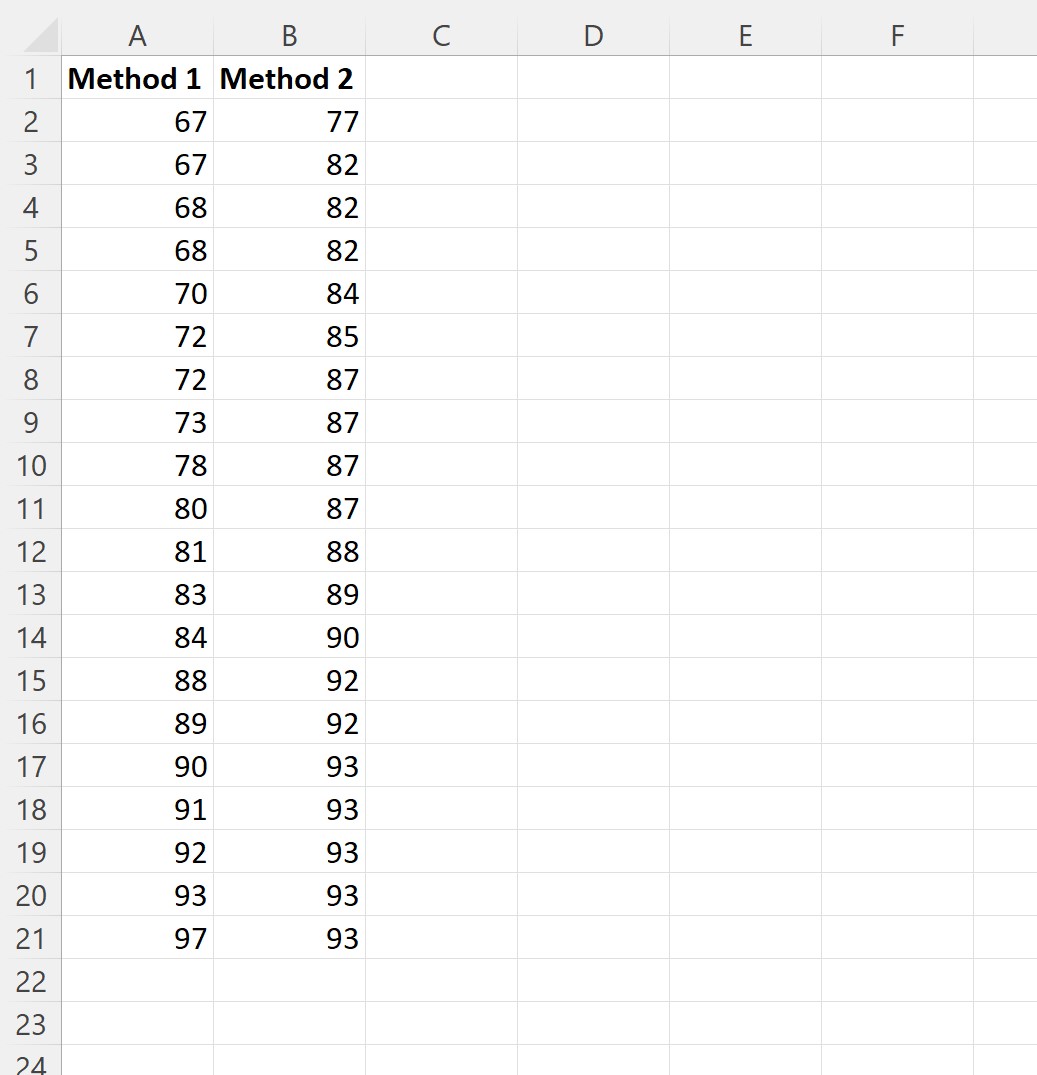
Étape 2 : Déterminer la variance égale ou inégale

Ensuite, nous pouvons calculer le rapport des variances de l’échantillon :

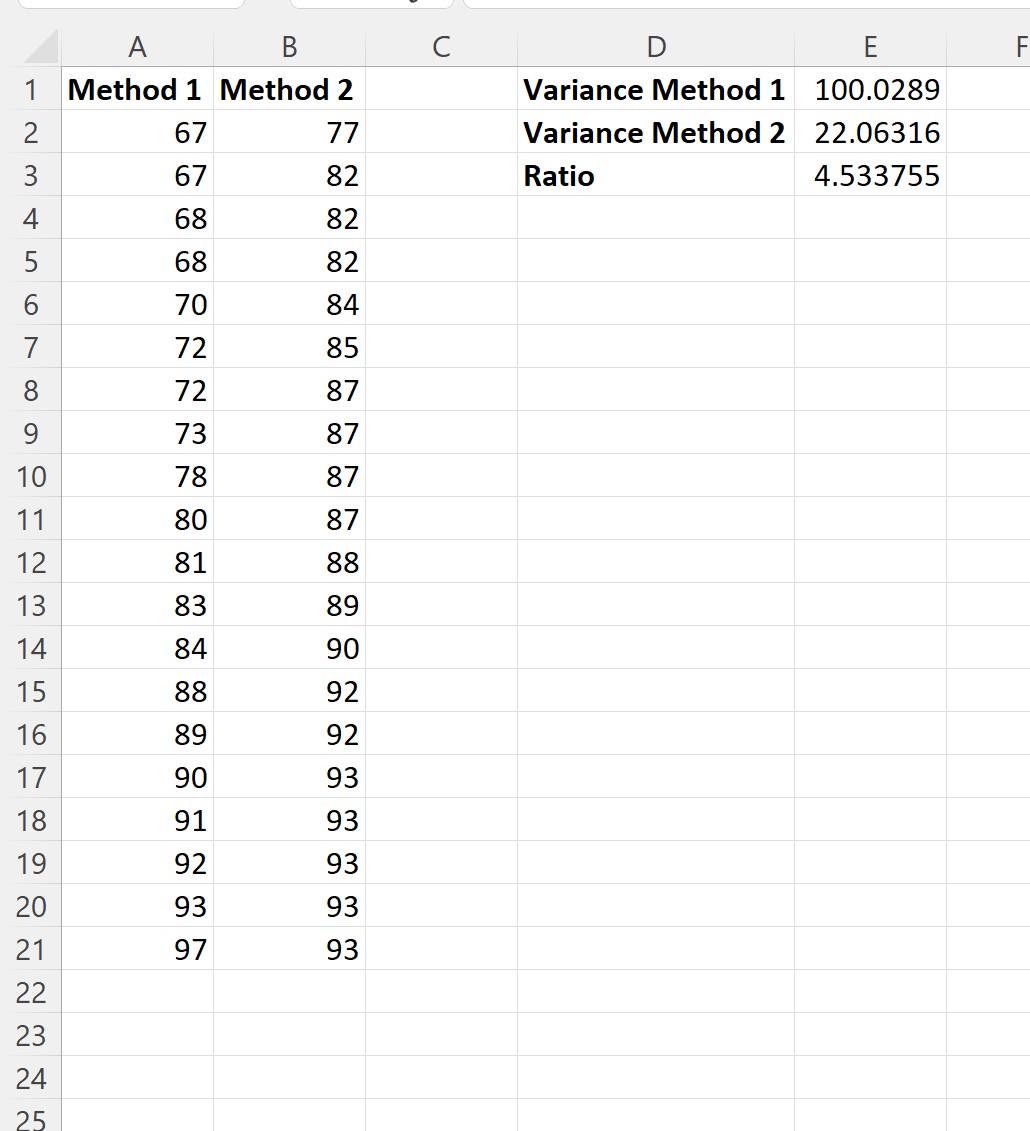
Voici les formules que nous avons tapées dans chaque cellule :

• Cellule E1 : =VAR.S(A2:A21)
• Cellule E2 : =VAR.S(B2:B21)
• Cellule E3 : =E1/E2

Nous pouvons voir que le rapport entre la plus grande variance de l’échantillon et la plus petite variance de l’échantillon est de 4,533755 .

Cette valeur étant supérieure ou égale à 4, nous supposons que les variances entre les deux échantillons ne sont pas égales.

Étape 3 : Effectuer un test t sur deux échantillons avec une variance inégale

Ensuite, nous pouvons effectuer un test t à deux échantillons avec des variances inégales pour déterminer si la note moyenne à l’examen entre les deux échantillons est égale.

Pour ce faire, cliquez sur l’onglet Données dans le ruban supérieur, puis cliquez sur le bouton Analyse des données dans le groupe Analyser :

Si vous ne voyez pas ce bouton, vous devez d’abord installer le Data Analysis Toolpak gratuit dans Excel .

Dans la nouvelle fenêtre qui apparaît, cliquez sur T-test : Two-Sample Assuming Unequal Variances , puis cliquez sur OK :

Dans la nouvelle fenêtre qui apparaît, renseignez les informations suivantes, puis cliquez sur OK :

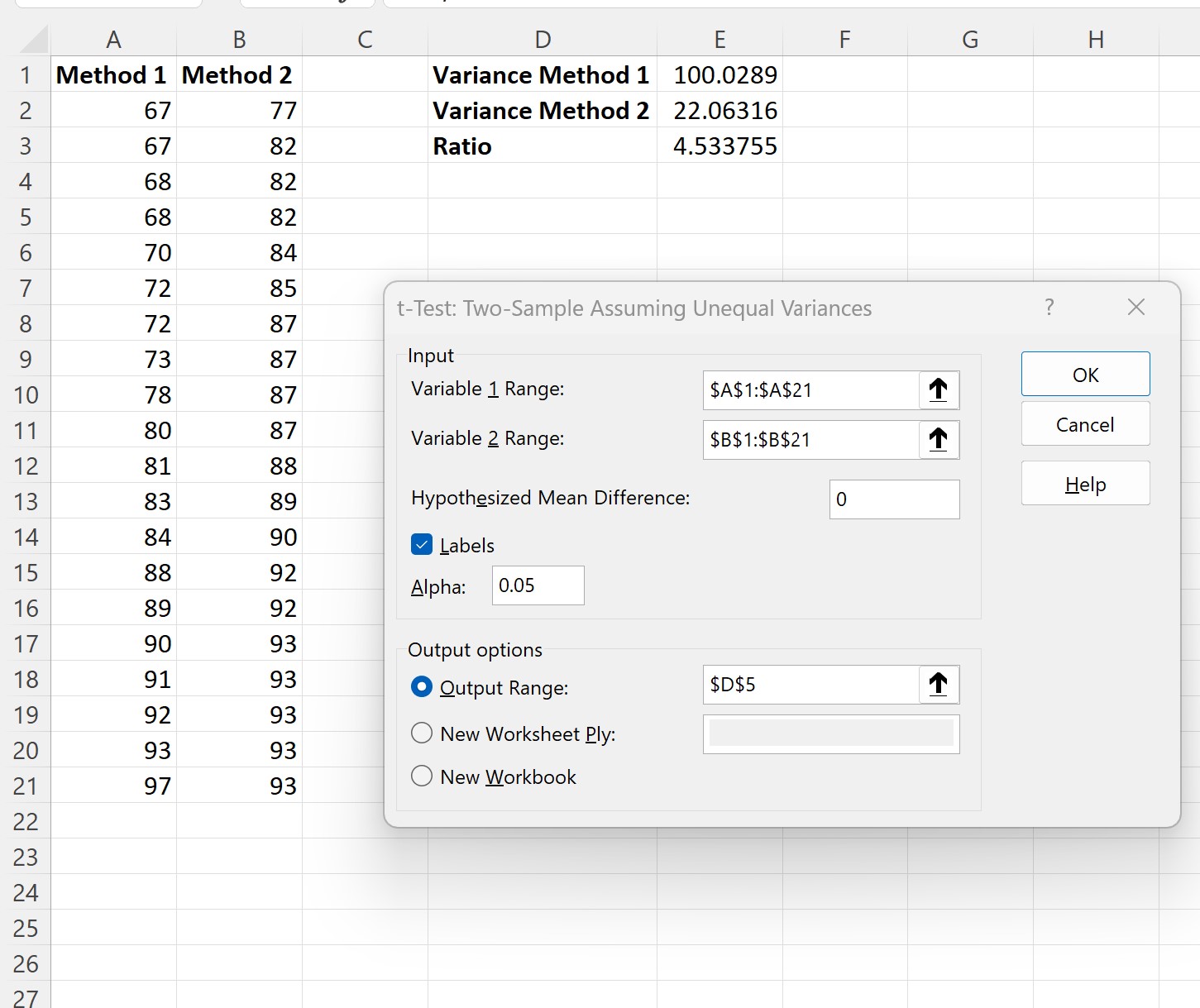
Une fois que vous avez cliqué sur OK , les résultats des deux exemples de tests t apparaîtront :

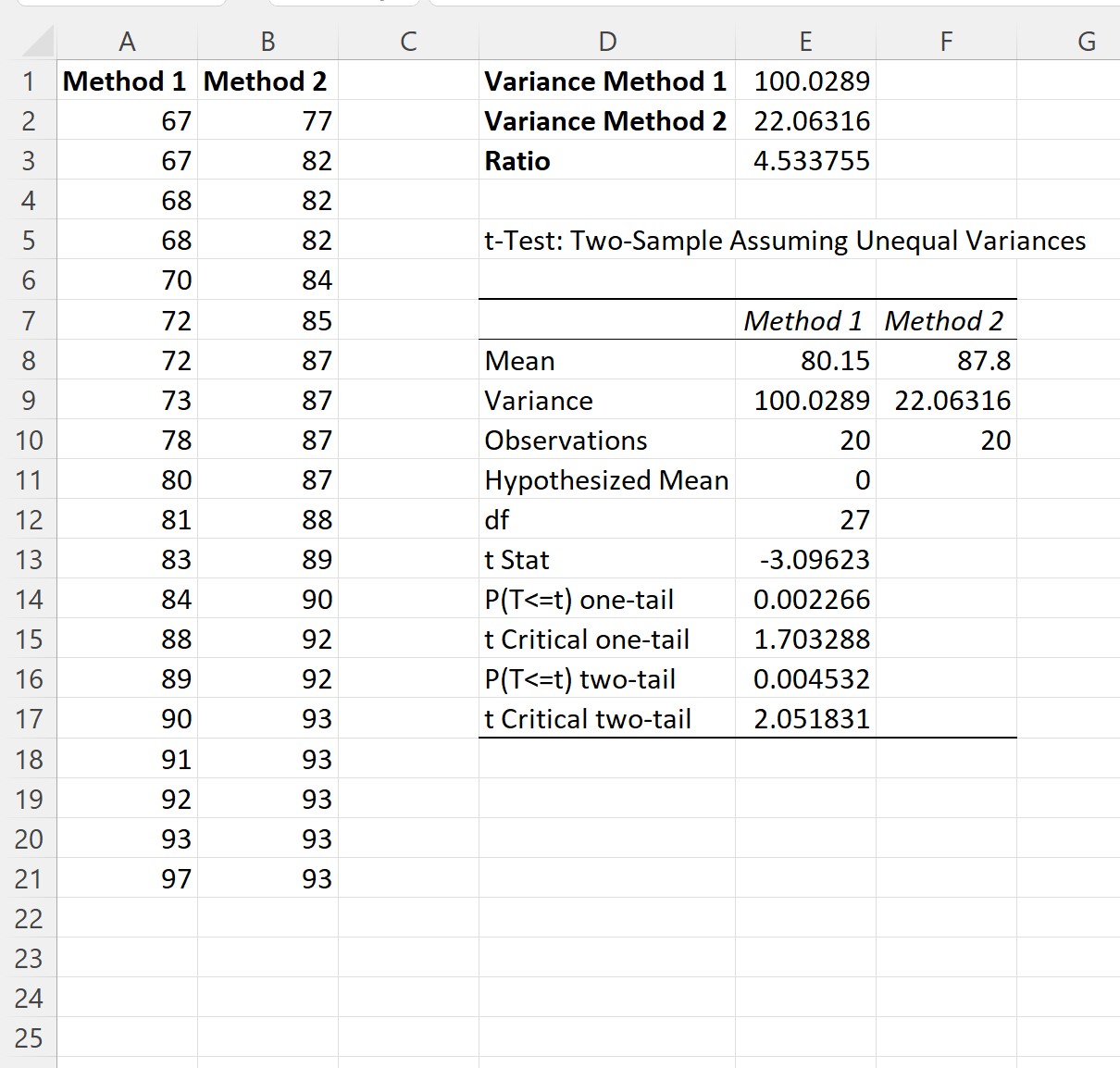
Étape 4 : Interpréter les résultats

À partir du résultat, nous pouvons voir :

• La note moyenne à l’examen pour la méthode 1 était de 80,15 .
• La note moyenne à l’examen pour la méthode 2 était de 87,8 .
• La statistique du test t était de -3,09623 .
• La valeur p bilatérale correspondante était de 0,004532 .

Étant donné que cette valeur p est inférieure à 0,05, nous pouvons conclure qu’il existe une différence statistiquement significative dans les résultats moyens aux examens entre les deux méthodes d’étude.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans Excel :

Comment effectuer un test t sur un échantillon dans Excel
Comment effectuer un test t pour échantillons appariés dans Excel
Comment effectuer un échantillon et deux échantillons de tests Z dans Excel