Fonction de densité
Dans cet article vous découvrirez ce qu’est la fonction de densité, comment une probabilité est calculée à partir de la fonction de densité et les caractéristiques de cette fonction probabiliste. De plus, vous pourrez voir quelles sont les différences entre la fonction de densité et la fonction de distribution.
Quelle est la fonction de densité ?
La fonction de densité , également appelée fonction de densité de probabilité , est une fonction mathématique qui décrit la probabilité qu’une variable aléatoire continue prenne une certaine valeur.
Autrement dit, la fonction de densité associée à une variable définit mathématiquement les probabilités que la variable prenne une valeur.
Par exemple, imaginons que la probabilité qu’une personne adulte mesure plus de 1,80 m dans une population est de 35 %, alors la fonction de densité indiquera une probabilité de 35 % lors du calcul de ladite probabilité.
Parfois, la fonction de densité de probabilité est abrégée par l’abréviation PDF.
Calculer une probabilité avec la fonction de densité
Pour trouver la probabilité qu’une variable continue prenne une valeur dans un intervalle, il faut calculer l’intégrale de la fonction de densité associée à ladite variable entre les limites de l’intervalle.
![]()
Où
![]() est la fonction de densité de la variable aléatoire continue.
est la fonction de densité de la variable aléatoire continue.
Ou en d’autres termes, la probabilité que la variable prenne une valeur dans un intervalle est équivalente à l’aire sous la fonction de densité dans cet intervalle.
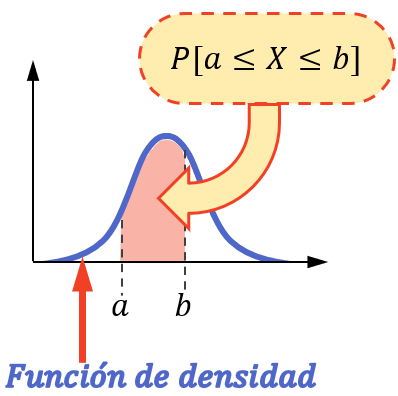
Notez que le calcul de probabilité ne peut être effectué de cette manière que si la variable statistique suit une distribution continue, comme la distribution normale, la distribution exponentielle, la distribution de Poisson, etc.
Propriétés de la fonction de densité
La fonction de densité a les propriétés suivantes :
- La valeur de la fonction de densité est nulle ou positive pour toute valeur de x.
![]()
- De plus, la valeur maximale de la fonction de densité est égale à 1.
![]()
- En fait, l’aire totale sous le graphique de la fonction de densité est toujours équivalente à 1 quelle que soit la variable, puisqu’elle correspond à l’ensemble de toutes les probabilités.
![]()
- Comme expliqué dans la section précédente, la probabilité qu’une variable continue prenne une valeur dans un intervalle est calculée avec l’intégrale de la fonction de densité dans cet intervalle.
![]()
Fonction de densité et fonction de distribution
Dans cette dernière section, nous verrons en quoi la fonction de densité et la fonction de distribution diffèrent, puisqu’il s’agit de deux types de fonctions probabilistes que l’on confond généralement.
Mathématiquement, la fonction de distribution est équivalente à l’intégrale de la fonction de densité , donc la fonction de distribution décrit la probabilité cumulée d’une variable continue.
Autrement dit, l’image de la fonction de distribution pour toute valeur est égale à la probabilité que la variable prenne cette valeur ou une valeur inférieure.
La relation mathématique entre ces deux types de fonctions est donc la suivante :
![]()
Où
![]() est la fonction de densité et
est la fonction de densité et![]() est la fonction de distribution.
est la fonction de distribution.
Remarquez comment la représentation graphique de la fonction de densité change par rapport à sa fonction de distribution d’une variable qui suit une distribution normale avec une moyenne de 1 et un écart type de 0,5 :

Pour en savoir plus sur la fonctionnalité de distribution, cliquez sur le lien ci-dessous :
