Fonction de probabilité

Cet article explique ce que sont les fonctions de probabilité. Ainsi, vous trouverez la signification d’une fonction de probabilité, ses propriétés et un exemple concret de calcul d’une fonction de probabilité. De plus, les différences entre une fonction de probabilité et d’autres types de fonctions probabilistes sont présentées.

Qu’est-ce qu’une fonction de probabilité ?

Une fonction de probabilité , également appelée fonction de masse de probabilité , est une fonction mathématique qui décrit la probabilité qu’une variable aléatoire discrète prenne une certaine valeur.

Autrement dit, une fonction de probabilité renvoie la probabilité associée à une variable discrète d’être exactement égale à une valeur.

Par exemple, la probabilité d’obtenir n’importe quel nombre en lançant un dé est de 1/6 (un dé a six faces), par conséquent, la fonction de probabilité associée à cet espace échantillon sera égale à 1/6 pour n’importe quelle valeur.

Propriétés de la fonction de probabilité

Les fonctions de probabilité ont les propriétés suivantes :

• Les probabilités ne peuvent pas être négatives, donc la fonction de probabilité est nulle ou positive pour toute valeur de x.

• De même, la probabilité maximale est l’unité, ce qui signifie que l’événement se produira toujours. Par conséquent, la valeur maximale de la fonction de probabilité est égale à 1.

• Enfin, la somme de toutes les valeurs d’une fonction de probabilité donne 1, puisqu’il s’agit de la somme de toutes les probabilités de l’espace échantillon.

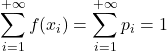
Exemple de fonction de probabilité

Maintenant que nous connaissons la définition et les caractéristiques de la fonction de probabilité, voyons un exemple de ce type de fonction probabiliste.

• Calculez les probabilités d’obtenir face 0, 1, 2, 3 et 4 fois en effectuant quatre lancers de pièces indépendants. Ensuite, représentez graphiquement la fonction de probabilité trouvée.

Tout d’abord, il faut calculer les probabilités d’obtenir face, pour ce faire, il faut diviser les cas possibles par le nombre total de cas. Vous pouvez voir le calcul de toutes les probabilités dans le tableau suivant :

Et une fois qu’on a calculé toutes les probabilités, on peut représenter les valeurs de la fonction de probabilité sur un graphique :

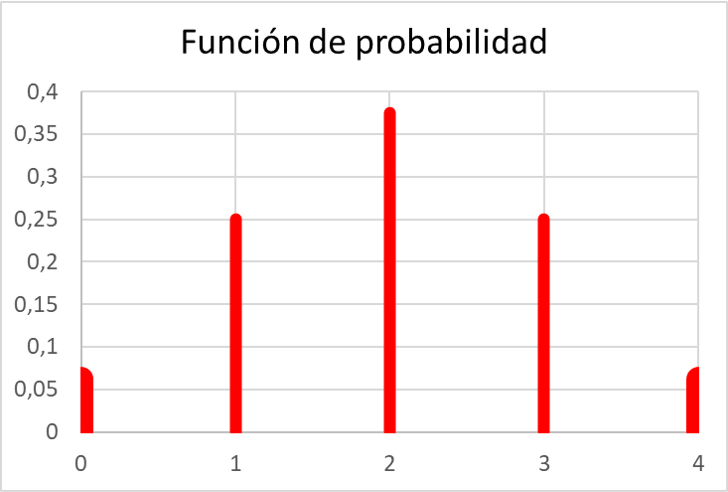
Comme vous pouvez le constater, la fonction probabiliste de l’exercice répond à toutes les propriétés des fonctions de probabilité, puisque toutes ses valeurs sont comprises entre 0 et 1 et, de plus, la somme de toutes ses valeurs est équivalente à 1.

Fonction de probabilité et fonction de densité

Dans cette section, nous verrons la différence entre la fonction de probabilité et la fonction de densité, car ce sont deux types de fonctions probabilistes qui ont le même objectif mais sont utilisées dans des cas différents.

La différence entre la fonction de probabilité et la fonction de densité est le type de variable pour laquelle les probabilités décrivent. La fonction de probabilité est utilisée pour définir les probabilités d’une variable discrète, tandis que la fonction de densité est utilisée pour définir les probabilités d’une variable continue.

Ainsi, selon la variable, une fonction de probabilité ou une fonction de densité est utilisée.

Pour en savoir plus sur la fonction densité, cliquez sur le lien suivant :

Fonction de probabilité et fonction de distribution

La différence entre une fonction de probabilité et une fonction de distribution réside dans le type de probabilité qu’elles définissent. La fonction de probabilité indique la probabilité que la variable prenne une certaine valeur, tandis que la fonction de distribution décrit la probabilité cumulée de la variable.

Par conséquent, la fonction de distribution est calculée à partir de la fonction de probabilité.

À titre d’exemple, dans le lien suivant, vous pouvez voir le calcul de la fonction de distribution pour obtenir face à partir de quatre lancers de pièces, basé sur la fonction de probabilité trouvée dans l’exercice ci-dessus.