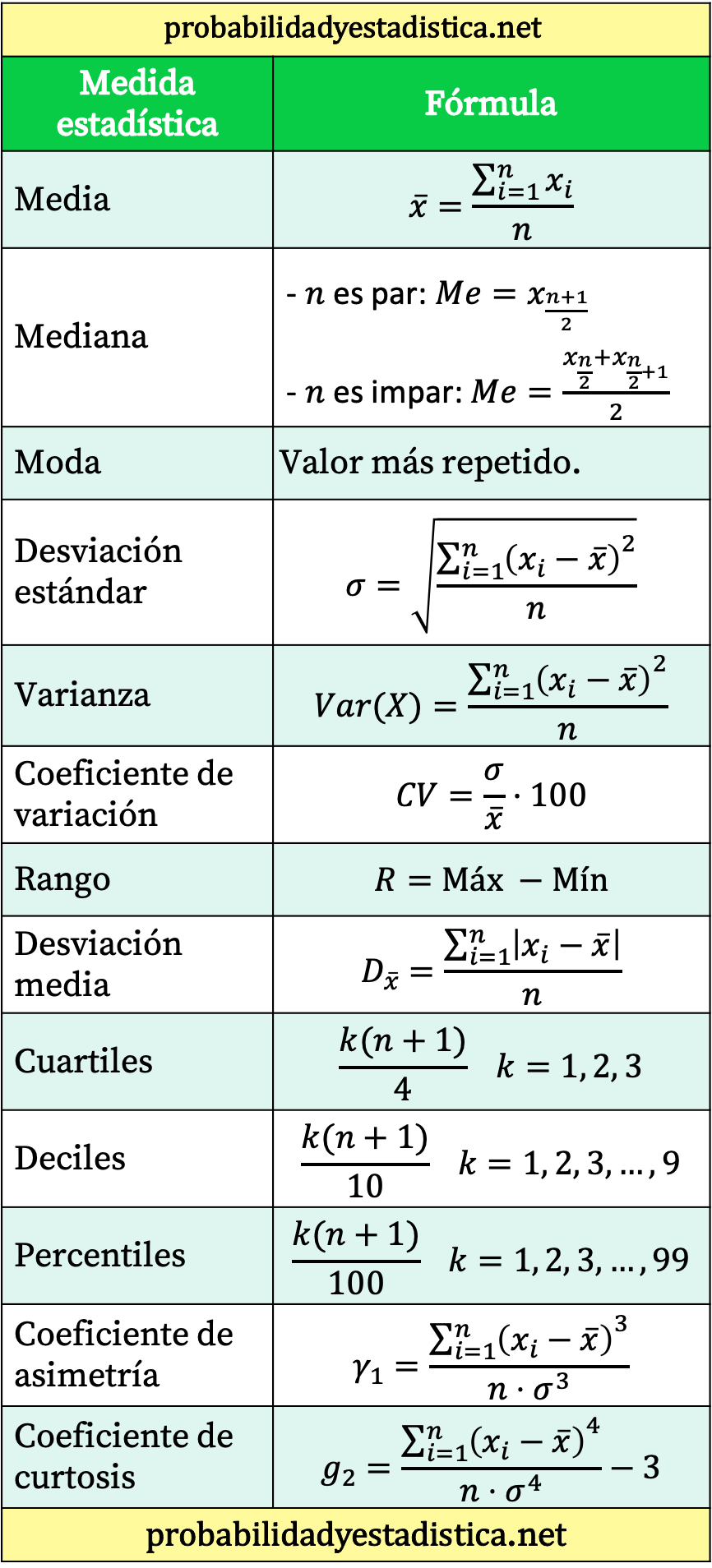
Formules statistiques

Par août 1, 2023 Statistiques 0 commentaire

Vous trouverez ici les principales formules statistiques. Nous vous laissons également lié à nos articles dans lesquels vous pouvez voir des exemples d’application de chaque formule statistique et, en plus, vous pouvez utiliser une calculatrice en ligne pour ne pas avoir à faire les calculs et connaître le résultat du formule directement.

Formules pour les mesures statistiques de tendance centrale

Moitié

Pour calculer la moyenne, il faut additionner toutes les valeurs puis diviser par le nombre total de données. La formule de la moyenne est donc la suivante :

\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}

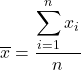
En statistique, la moyenne est également connue sous le nom de moyenne arithmétique ou moyenne .

Médian

La médiane est la valeur médiane de toutes les données classées de la plus petite à la plus grande. Autrement dit, la médiane divise l’ensemble des données ordonnées en deux parties égales.

Le calcul de la médiane dépend du fait que le nombre total de données soit pair ou impair :

  • Si le nombre total de données est impair , la médiane sera la valeur qui se situe en plein milieu des données. C’est-à-dire la valeur qui se trouve en position (n+1)/2 des données triées.

    • Me=x_{\frac{n+1}{2}

  • Si le nombre total de données est pair , la médiane sera la moyenne des deux données situées au centre. C’est-à-dire la moyenne arithmétique des valeurs qui se trouvent aux positions n/2 et n/2+1 des données ordonnées.

    • Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}

Où

n est le nombre total de données dans l’échantillon et le symbole Me indique la médiane.

➤ Voir : Calculateur médian

Mode

En statistiques, le mode est la valeur de l’ensemble de données qui a la fréquence absolue la plus élevée, c’est-à-dire que le mode est la valeur la plus répétée dans un ensemble de données.

Par conséquent, il n’existe pas de formule spécifique pour le mode, mais pour calculer le mode d’un ensemble de données statistiques, il suffit de compter le nombre de fois où chaque élément de données apparaît dans l’échantillon, et les données les plus répétées seront le mode.

Le mode peut également être dit mode statistique ou valeur modale .

➤ Voir : Calculateur de mode

Formules pour les mesures statistiques de dispersion

Écart-type

L’écart type, également appelé écart type, est égal à la racine carrée de la somme des carrés des écarts de la série de données divisée par le nombre total d’observations.

Par conséquent, la formule de l’écart type est la suivante :

\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}

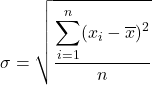
Variance

La variance est égale à la somme des carrés des résidus sur le nombre total d’observations. La formule de cette métrique statistique est donc la suivante :

Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}

Où:

  • X est la variable aléatoire pour laquelle vous souhaitez calculer la variance.
  • x_i est la valeur des donnéesi .
  • n est le nombre total d’observations.
  • \overline{X} est la moyenne de la variable aléatoireX .

Coefficient de variation

En statistique, le coefficient de variation est une mesure de dispersion utilisée pour déterminer la dispersion d’un ensemble de données par rapport à sa moyenne. Le coefficient de variation est calculé en divisant l’écart type des données par sa moyenne, puis en multipliant par 100 pour exprimer la valeur en pourcentage.

CV=\cfrac{\sigma}{\overline{x}}\cdot 100

Gamme

La plage statistique est une mesure de dispersion qui indique la différence entre la valeur maximale et la valeur minimale des données dans un échantillon. Par conséquent, pour calculer l’étendue d’une population ou d’un échantillon statistique, la valeur maximale doit être soustraite de la valeur minimale.

R=\text{M\'ax}-\text{M\'in}

Gamme interquartile

L’ intervalle interquartile , également appelé intervalle interquartile , est une mesure de dispersion statistique qui indique la différence entre le troisième et le premier quartile.

Par conséquent, pour calculer l’intervalle interquartile d’un ensemble de données statistiques, vous devez d’abord trouver les troisième et premier quartiles, puis les soustraire.

IQR=Q_3-Q_1

écart moyen

L’ écart moyen , également appelé écart absolu moyen , est la moyenne des écarts absolus. L’écart moyen est donc égal à la somme des écarts de chaque donnée par rapport à la moyenne arithmétique divisée par le nombre total de données.

D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}

Formules pour les mesures statistiques de position

quartiles

En statistiques, les quartiles sont les trois valeurs qui divisent un ensemble de données ordonnées en quatre parties égales. Ainsi, les premier, deuxième et troisième quartiles représentent respectivement 25 %, 50 % et 75 % de l’ensemble des données statistiques.

Les quartiles sont représentés par un Q majuscule et l’indice du quartile, de sorte que le premier quartile est Q 1 , le deuxième quartile est Q 2 et le troisième quartile est Q 3 .

La formule quartile est la suivante :

\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3

Attention : cette formule nous indique la position du quartile, pas la valeur du quartile. Le quartile sera la donnée située à la position obtenue par la formule.

Cependant, parfois le résultat de cette formule nous donnera un nombre décimal. Il faut donc distinguer deux cas selon que le résultat est un nombre décimal ou non :

  • Si le résultat de la formule est un nombre sans partie décimale , le quartile est la donnée qui se trouve dans la position fournie par la formule ci-dessus.
  • Si le résultat de la formule est un nombre avec une partie décimale , la valeur du quartile est calculée à l’aide de la formule suivante :

Q=x_i+d\cdot (x_{i+1}-x_i)

Où x i et x i+1 sont les nombres des positions entre lesquelles se trouve le nombre obtenu par la première formule, et d est la partie décimale du nombre obtenu par la première formule.

déciles

En statistiques, les déciles sont les neuf valeurs qui divisent un ensemble de données ordonnées en dix parties égales. De sorte que le premier, deuxième, troisième,… décile représente 10%, 20%, 30%,… de l’échantillon ou de la population.

Les déciles sont représentés par la lettre majuscule D et l’indice du décile, c’est-à-dire que le premier décile est D 1 , le deuxième décile est D 2 , le troisième décile est D 3 , etc.

La formule des déciles est la suivante :

\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9

Attention : cette formule nous indique la position du décile, pas la valeur du décile. Le décile sera la donnée située à la position obtenue par la formule.

Cependant, parfois le résultat de cette formule nous donnera un nombre décimal, il faut donc distinguer deux cas selon que le résultat est un nombre décimal ou non :

  • Si le résultat de la formule est un nombre sans partie décimale , le décile est la donnée qui se trouve dans la position fournie par la formule ci-dessus.
  • Si le résultat de la formule est un nombre avec une partie décimale , la valeur du décile est calculée à l’aide de la formule suivante :

D=x_i+d\cdot (x_{i+1}-x_i)

Où x i et x i+1 sont les nombres des positions entre lesquelles se trouve le nombre obtenu par la première formule, et d est la partie décimale du nombre obtenu par la première formule.

percentiles

En statistiques, les percentiles sont les valeurs qui divisent un ensemble de données ordonnées en cent parties égales. Ainsi, un percentile indique la valeur en dessous de laquelle se situe un pourcentage de l’ensemble de données.

Les centiles sont représentés par la lettre majuscule P et l’indice du centile, c’est-à-dire que le premier centile est P 1 , le 40e centile est P 40 , le 79e centile est P 79 , etc.

La formule du percentile est la suivante :

\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99

Attention : cette formule nous indique la position du percentile, mais pas sa valeur. Le percentile sera la donnée située à la position obtenue par la formule.

Cependant, parfois le résultat de cette formule nous donnera un nombre décimal, il faut donc distinguer deux cas selon que le résultat est un nombre décimal ou non :

  • Si le résultat de la formule est un nombre sans partie décimale , le centile correspond aux données qui se trouvent dans la position fournie par la formule ci-dessus.
  • Si le résultat de la formule est un nombre avec une partie décimale , la valeur exacte du percentile est calculée à l’aide de la formule suivante :

P=x_i+d\cdot (x_{i+1}-x_i)

Où x i et x i+1 sont les nombres des positions entre lesquelles se trouve le nombre obtenu par la première formule, et d est la partie décimale du nombre obtenu par la première formule.

Formules de mesure statistique de forme

coefficient d’asymétrie

Le coefficient d’asymétrie, ou indice d’asymétrie, est un coefficient statistique utilisé pour déterminer l’asymétrie d’une distribution. Ainsi, en calculant le coefficient d’asymétrie, vous pouvez connaître le type d’asymétrie de la distribution sans avoir à en faire une représentation graphique.

La formule du coefficient d’asymétrie est la suivante :

\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}

De manière équivalente, l’une ou l’autre des deux formules suivantes peut être utilisée pour calculer le coefficient d’asymétrie de Fisher :

\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}

\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}

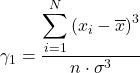
Où

E est l’espérance mathématique,\overline{x} la moyenne arithmétique,\sigma l’écart type etn le nombre total de données.

coefficient d’aplatissement

L’aplatissement, également appelé netteté, indique le degré de concentration d’une distribution autour de sa moyenne. Autrement dit, l’aplatissement indique si une distribution est raide ou plate. Plus précisément, plus l’aplatissement d’une distribution est élevé, plus elle est raide (ou pointue).

La formule du coefficient d’aplatissement est la suivante :

\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3

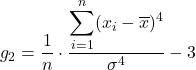
Où

x_i est la valeur correspondant à l’observationi ,\overline{x} la moyenne arithmétique,\sigma l’écart type etn le nombre total de données.

Tableau récapitulatif de toutes les formules statistiques

Enfin, nous vous laissons un tableau qui résume les principales formules statistiques.

formules statistiques

à propos de l'auteur

Amelia Rodriguez
Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus

Ajouter un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *