Fréquence cumulative

Cet article explique ce qu’est la fréquence cumulée dans les statistiques. Ainsi, vous découvrirez la signification de la fréquence cumulée, comment la fréquence cumulée est calculée avec des exemples et, enfin, les différents types de fréquences cumulées qu’il existe.

Qu’est-ce que la fréquence cumulée ?

En statistiques, la fréquence cumulée est la somme cumulée des fréquences. Autrement dit, la fréquence cumulée d’une valeur est égale à la fréquence de cette valeur plus les fréquences de toutes les valeurs inférieures.

On distingue deux types de fréquences cumulées : la fréquence absolue cumulée et la fréquence relative cumulée. Ci-dessous, nous verrons comment chaque type de fréquence cumulée est calculé.

Gardez à l’esprit que pour comprendre ce que signifie la fréquence cumulée dans les statistiques, vous devez d’abord être clair sur le concept de fréquence. C’est pourquoi il est recommandé de visiter le post suivant avant de poursuivre l’explication :

Comment calculer la fréquence cumulée

Les étapes pour calculer la fréquence cumulée d’un échantillon statistique sont :

1. Créez un tableau avec toutes les différentes valeurs qui apparaissent dans l’ensemble de données, classées de la plus petite à la plus grande.
2. Trouvez la fréquence absolue de chaque valeur.
3. Trouvez la fréquence cumulée de chaque valeur, qui est calculée en additionnant la fréquence de la valeur elle-même plus les fréquences de toutes les valeurs plus petites.

Par conséquent, la formule pour calculer la fréquence cumulée est la suivante :

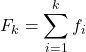
Où:

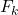• est la fréquence cumulée de la valeur .
• est la fréquence absolue de la valeur .

Notez que ces étapes servent à calculer la fréquence absolue cumulée, mais il existe également une fréquence relative cumulée. Ci-dessous, nous verrons la différence entre ces deux types de fréquences accumulées et comment chaque type est trouvé.

Types de fréquences cumulées

En statistiques, il existe deux types de fréquences cumulées :

• Fréquence absolue cumulée : c’est la somme cumulée des fréquences absolues .
• Fréquence relative cumulée : c’est la somme cumulée des fréquences relatives .

Compte tenu de la définition de chaque type de fréquence accumulée, vous pouvez voir ci-dessous un exemple de la façon dont chacune est obtenue.

Fréquence absolue cumulée

La fréquence absolue cumulée est représentée par le symbole F _i et est calculée en additionnant les fréquences absolues de valeurs égales ou inférieures à la valeur en question. Ensuite, vous disposez d’un exemple concret dans lequel la fréquence absolue cumulée d’un ensemble de données statistiques est calculée.

• Les notes obtenues dans la matière statistique dans une classe de 30 étudiants sont les suivantes. Quelle est la fréquence absolue cumulée de chaque note ?

Puisque tous les nombres ne peuvent être que des entiers, il s’agit d’une variable discrète. Il n’est donc pas nécessaire de regrouper les données en intervalles.

Ainsi, pour déterminer la fréquence absolue cumulée, nous devons d’abord trouver la fréquence absolue de chaque valeur, qui correspond au nombre de fois où chaque valeur apparaît dans l’échantillon statistique.

Maintenant que nous connaissons la fréquence absolue de chaque valeur, nous pouvons calculer leurs fréquences absolues cumulées. Pour ce faire, nous avons deux options : soit on additionne la fréquence absolue de la valeur plus toutes les fréquences absolues des plus petites valeurs, soit au contraire, on additionne la fréquence absolue de la valeur plus la fréquence absolue cumulée des valeurs précédentes. valeur.

En bref, le tableau avec la fréquence cumulée absolue de l’exercice est le suivant :

Notez que la fréquence absolue accumulée de la dernière valeur coïncide toujours avec le nombre total de données. Sinon, cela signifie que vous avez commis une erreur dans le calcul.

Fréquence relative cumulée

La fréquence relative cumulée est représentée par le symbole H _i et est calculée en additionnant les fréquences relatives de valeurs égales ou inférieures à la valeur en question. Ci-dessous, vous pouvez voir un exercice résolu avec les mêmes données que le problème précédent dans lequel la fréquence relative cumulée est déterminée.

• Les notes obtenues en matière de statistiques dans une classe de 30 étudiants sont les suivantes. Quelle est la fréquence relative cumulée de chaque note ?

Dans ce cas, la variable est discrète, puisqu’elle ne peut pas prendre de valeur décimale. Il n’est donc pas nécessaire de regrouper les données par intervalles, mais nous pouvons effectuer les calculs directement.

Ainsi, nous dressons un tableau de fréquences et déterminons la fréquence absolue de chaque valeur différente :

Ensuite, nous calculons la fréquence relative de chaque valeur, qui est déterminée en divisant la fréquence absolue par le nombre total d’observations (30).

Et une fois que nous avons calculé la fréquence absolue et la fréquence relative de l’ensemble de données, nous pouvons obtenir la fréquence relative cumulée. Pour ce faire, il faut additionner la fréquence relative de la valeur en question plus toutes les fréquences relatives précédentes ou, ce qui revient au même, la fréquence relative accumulée précédente :

En bref, le tableau des fréquences avec la fréquence absolue, la fréquence relative et la fréquence relative cumulée est le suivant :

Gardez à l’esprit que la dernière valeur de la fréquence relative cumulée doit toujours être 1. Si vous obtenez un autre nombre, cela signifie que vous avez commis une erreur dans les calculs.