Fréquence (statistique)

Cet article explique en quoi consiste la notion de fréquence en statistique. Ainsi, vous trouverez la définition de la fréquence dans les statistiques, les différents types de fréquences qui existent et, enfin, comment réaliser un tableau de fréquences.

Qu’est-ce que la fréquence dans les statistiques ?

En statistiques, la fréquence est le nombre de fois qu’une valeur apparaît dans un ensemble de données. Autrement dit, la fréquence est le nombre de fois qu’une valeur est répétée dans un échantillon statistique.

Par exemple, si dans une enquête cinq personnes ont répondu que leur couleur préférée est le bleu, alors la fréquence de la couleur bleue est égale à 5.

Généralement, en statistiques, la lettre f avec l’indice i est utilisée pour représenter la fréquence de la valeur i , donc le symbole de la fréquence est _fi .

La somme de toutes les fréquences donne le nombre total de données dans l’échantillon. Par conséquent, la formule suivante est toujours valable pour toute étude statistique :

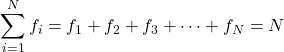
Où

est la fréquence de la valeur et est le nombre total d’observations.

Types de fréquences dans les statistiques

En statistiques, les différents types de fréquences sont les suivants :

• Fréquence absolue : correspond au nombre de fois qu’une valeur apparaît dans un échantillon statistique.
• Fréquence absolue cumulée : calculée en ajoutant la fréquence absolue de la valeur plus les fréquences absolues de toutes les valeurs plus petites.
• Fréquence relative : c’est la fréquence absolue divisée par le nombre total de données.
• Fréquence relative cumulée : est égale à la somme de la fréquence relative de la valeur plus les fréquences relatives de toutes les valeurs inférieures.

Dans la section ci-dessous, vous pouvez voir comment chaque type de fréquence est calculé.

Tableau des fréquences

Généralement en statistiques, les calculs des fréquences d’un échantillon de données sont résumés dans un tableau de fréquences. Vous trouverez ci-dessous un exemple étape par étape afin que vous puissiez voir comment procéder.

• Les notes obtenues dans la matière statistique dans une classe de 30 étudiants sont les suivantes. Construisez un tableau de fréquence de l’ensemble de données.

Puisque tous les nombres ne peuvent être que des entiers, il s’agit d’une variable discrète. Il n’est donc pas nécessaire de regrouper les données en intervalles.

Nous devons donc construire un tableau dans lequel chaque valeur différente sera une ligne. De plus, il faut trouver la fréquence absolue de chaque valeur, pour cela, il suffit de compter le nombre de fois que la valeur apparaît dans l’échantillon de données.

Notez que la somme de toutes les fréquences absolues équivaut au nombre total de données. Si cette règle n’est pas respectée, cela signifie que vous avez oublié de renseigner certaines informations.

Maintenant que nous connaissons la fréquence absolue, nous devons trouver la fréquence absolue cumulée. Pour ce calcul nous avons deux options : soit on additionne la fréquence absolue de la valeur plus toutes les fréquences absolues des plus petites valeurs, soit au contraire, on additionne la fréquence absolue de la valeur plus la fréquence absolue cumulée de la valeur précédente .

La fréquence absolue cumulée de la dernière valeur correspond toujours au nombre total de données, vous pouvez utiliser cette astuce pour vérifier que les calculs sont corrects.

Ensuite, nous devons déterminer la fréquence relative, qui est calculée en divisant la fréquence absolue par le nombre total de données (30) :

Gardez à l’esprit que la somme de toutes les fréquences relatives est toujours égale à 1, sinon cela signifie que certains calculs dans le tableau des fréquences sont erronés.

Finalement, il suffit d’extraire la fréquence relative accumulée. Pour ce faire, il faut additionner la fréquence relative de la valeur en question plus toutes les fréquences relatives précédentes ou, ce qui revient au même, la fréquence relative accumulée précédente :

En bref, le tableau des fréquences avec toutes les fréquences des données problématiques est le suivant :