Rang (statistique)

Dans cet article, nous expliquons quelle est la plage dans les statistiques et comment elle est calculée. Vous trouverez un exercice résolu sur l’étendue d’un ensemble de données et, enfin, nous vous montrerons à quoi il sert et quand il doit être utilisé.

Qu’est-ce que la plage dans les statistiques ?

En statistiques, la plage est une mesure de dispersion qui indique la différence entre la valeur maximale et la valeur minimale des données d’un échantillon. Par conséquent, pour calculer l’étendue d’une population ou d’un échantillon statistique, la valeur maximale doit être soustraite de la valeur minimale.

Par exemple, si la valeur maximale d’un ensemble de données est 9 et la valeur minimale est 2, la plage de cet échantillon statistique est 7 (9-2=7).

La plage statistique est également appelée étendue ou plage de mesure.

Ainsi, la plage est une mesure de la dispersion avec la variance, l’écart type (ou écart type), l’écart moyen et le coefficient de variation.

Comment calculer la plage dans les statistiques

La plage d’un échantillon est calculée en soustrayant les valeurs extrêmes des données de l’échantillon statistique, c’est-à-dire que la plage d’un échantillon est égale à la valeur maximale de toutes les données moins la valeur minimale .

Par conséquent, la formule pour calculer la plage statistique d’un ensemble de données est la suivante :

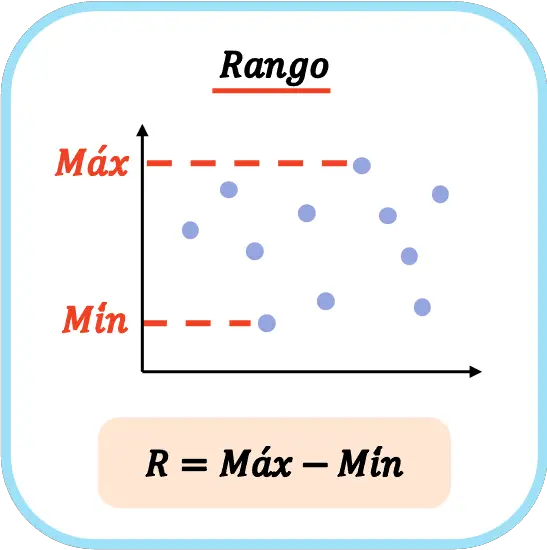
En statistiques, le symbole d’un R majuscule est souvent utilisé pour désigner l’étendue d’une série de données.

Le calcul de la plage d’un ensemble de données est donc assez simple, puisqu’il suffit de déterminer la différence entre les valeurs extrêmes. La seule chose à laquelle vous devez faire attention est d’obtenir les données maximales et minimales correctes et de ne pas oublier aucun chiffre.

Exemple de plage (statistique)

Après avoir vu la définition de la plage dans les statistiques, vous trouverez ci-dessous un exemple concret afin que vous puissiez voir comment la plage d’un ensemble de données est obtenue.

• Une entreprise souhaite analyser statistiquement les ventes réalisées par son produit phare au cours des vingt dernières années. Pour ce faire, ils vous demandent de calculer plusieurs mesures statistiques, dont le classement. Si les ventes du produit sont telles qu’indiquées dans le tableau suivant, quelle est la plage de cet ensemble de données ?

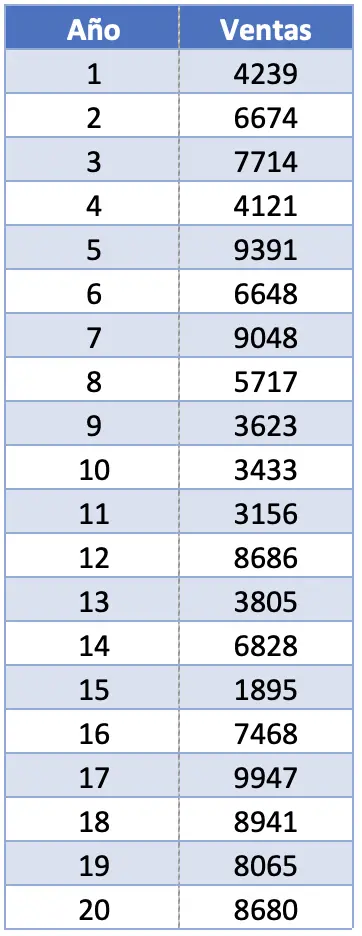
Dans cet exercice, nous avons 20 observations. En réalité, le nombre total d’observations ne fait aucune différence dans le calcul de l’étendue d’un échantillon, car nous ne nous intéressons qu’à la plus grande valeur et à la plus petite valeur.

Nous devons donc utiliser la formule vue ci-dessus pour trouver l’étendue de cet échantillon statistique.

La valeur maximale de l’intervalle est de 9947 unités vendues et la valeur minimale est de 1895. Par conséquent, nous devons soustraire ces deux valeurs pour trouver la plage de l’ensemble de données :

Cela signifie que la variation maximale survenue dans les ventes au cours des dernières années est de 8 052 unités. Ci-dessous, vous pouvez voir graphiquement toutes les données de l’exercice ainsi que leur plage statistique, le graphique vous aidera probablement à comprendre la signification de la plage.

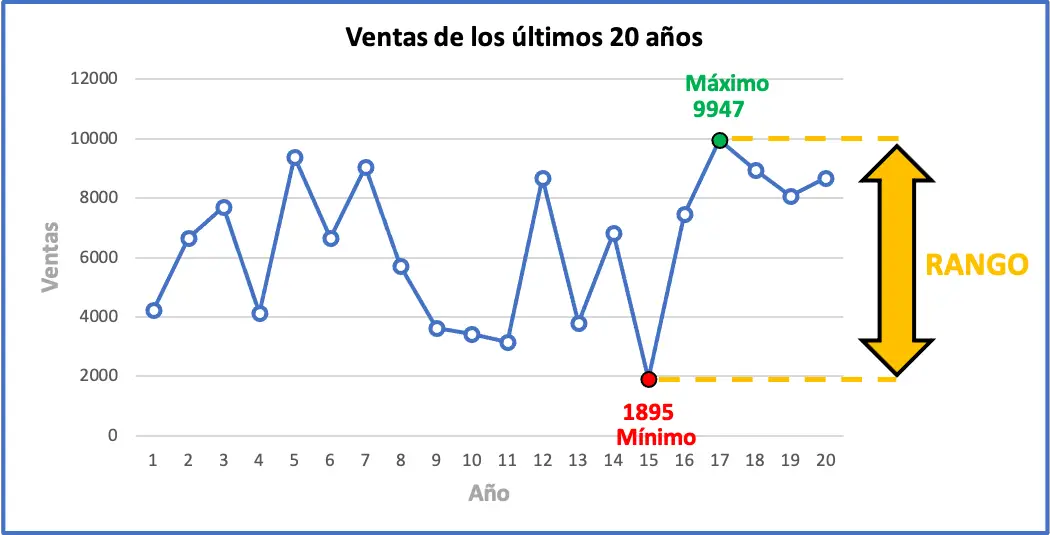
A quoi sert la plage des statistiques ?

Pour finir de comprendre la notion d’étendue en statistique, nous allons voir à quoi elle sert et comment interpréter cette mesure de dispersion.

En statistiques, la plage montre la différence entre la valeur maximale et la valeur minimale d’un ensemble de données. Par conséquent, la plage est une mesure qui sert à indiquer la dispersion totale d’un ensemble de données .

Lorsque vous connaissez la valeur de plage d’un ensemble de données, vous connaissez la différence maximale entre deux observations de cet ensemble, vous pouvez donc avoir une idée de si les données sont dispersées ou rapprochées. En général, il est intéressant que la portée soit la plus minimale possible, car cela signifie qu’il y a peu de dispersion et donc les calculs seront plus précis.

Par exemple, la plage peut être une mesure qui permet de faire la comparaison entre deux échantillons différents, car elle permet d’avoir une idée des dispersions des échantillons.

Il faut cependant être prudent dans l’interprétation de la plage statistique, car elle peut être trompeuse. Il se peut qu’un ensemble de données ait en réalité une très faible dispersion, mais s’il existe une valeur aberrante au sein de l’échantillon, la plage sera très large et ne reflétera donc pas correctement la dispersion de l’échantillon.

De plus, il n’en est pas de même pour un échantillon dont les valeurs sont de l’ordre des dizaines d’avoir un rang de 5, qu’un échantillon dont les valeurs sont de l’ordre des milliers d’avoir le même rang. Logiquement, même si les deux plages portent le même nombre, le premier échantillon est beaucoup plus dispersé que le second.

En conclusion, la plage est une mesure statistique utile pour analyser la dispersion d’un ensemble de données, mais pour interpréter correctement les données, d’autres métriques doivent également être calculées.